Промежуточные расчеты для оценки адекватности модели
| t | E(t) | [E(t)] 2 | E(t-1) | E(t) - E(t-1) | [E(t) -E(t-1)] 2 | E(t) * E(t-1) | E(t) / Y(t)% |
| -9,159 | 83,891 | — | — | — | — | -0,4362 | |
| 0,593 | 0,352 | -9,159 | 9,511 | 90,465 | -5,435 | 0,0228 | |
| 4,024 | 16,189 | 0,593 | 15,595 | 243,213 | 2,387 | 0,1387 | |
| 3,393 | 11,509 | 4,024 | 7,486 | 56,037 | 13,650 | 0,1060 | |
| 4,239 | 17,970 | 3,393 | 14,578 | 212,510 | 14,381 | 0,1116 | |
| 1,049 | 1,100 | 4,239 | -3,139 | 9,854 | 4,446 | 0,0269 | |
| 3,381 | 11,431 | 1,049 | 10,383 | 107,797 | 3,546 | 0,0768 | |
| 6,191 | 38,331 | 3,381 | 34,950 | 1221,496 | 20,933 | 0,1264 | |
| 0,803 | 0,645 | 6,191 | -5,547 | 30,766 | 4,970 | 0,0175 | |
| -4,682 | 21,924 | 0,803 | 21,122 | 446,121 | -3,759 | -0,1115 | |
| 0,836 | 0,698 | -4,682 | 5,381 | 28,951 | -3,913 | 0,0182 | |
| 7,149 | 51,112 | 0,836 | 50,277 | 2527,763 | 5,974 | 0,1521 | |
| -6,730 | 45,292 | 7,149 | 38,143 | 1454,852 | -48,114 | -0,2588 | |
| 4,443 | 19,741 | -6,730 | 26,471 | 700,691 | -29,901 | 0,1388 | |
| 3,924 | 15,401 | 4,443 | 10,958 | 120,077 | 17,436 | 0,1266 | |
| -5,995 | 35,940 | 3,924 | 32,016 | 1025,000 | -23,527 | -0,2398 | |
| 2,441 | 5,958 | -5,995 | 11,953 | 142,881 | -14,634 | 0,0626 | |
| 1,925 | 3,705 | 2,441 | 1,264 | 1,599 | 4,699 | 0,0448 | |
| 0,060 | 0,004 | 1,925 | -1,921 | 3,691 | 0,116 | 0,0014 | |
| 2,715 | 7,372 | 0,060 | 7,312 | 53,460 | 0,164 | 0,0554 | |
| 4,157 | 17,285 | 2,715 | 14,570 | 212,271 | 11,288 | 0,0784 | |
| -0,422 | 0,178 | 4,157 | -3,979 | 15,833 | -1,756 | -0,0084 | |
| 1,241 | 1,541 | -0,422 | 1,963 | 3,853 | -0,524 | 0,0248 | |
| 5,999 | 35,984 | 1,241 | 34,743 | 1207,094 | 7,446 | 0,1224 | |
| -7,301 | 53,299 | 5,999 | 47,300 | 2237,295 | -43,794 | -0,2607 | |
| 0,293 | 0,086 | -7,301 | 7,386 | 54,557 | -2,137 | 0,0098 | |
| -0,175 | 0,031 | 0,293 | -0,262 | 0,069 | -0,051 | -0,0060 | |
| -2,383 | 5,677 | -0,175 | 5,851 | 34,237 | 0,416 | -0,0769 | |
| -8,357 | 69,843 | -2,383 | 72,226 | 5216,548 | 19,911 | -0,2696 | |
| -3,199 | 10,233 | -8,357 | 18,591 | 345,607 | 26,734 | -0,0780 | |
| -7,260 | 52,713 | -3,199 | 55,912 | 3126,192 | 23,226 | -0,1815 | |
| -2,761 | 7,623 | -7,260 | 14,883 | 221,508 | 20,045 | -0,0587 | |
| -3,488 | 12,165 | -2,761 | 14,926 | 222,786 | 9,630 | -0,0712 | |
| -8,162 | 66,623 | -3,488 | 70,111 | 4915,597 | 28,469 | -0,1774 | |
| ИТОГО | -11,218 | 721,847 | -8,162 | 730,010 | 26290,672 | 62,324 | -0,7729 |
По таблице критерий Дарбина-Уотсона (Приложение 2) находим значение d1 и d2 для п = 34. Для нашего ряда d1= 1,39, d2 = 1,51, тогда
d > d2; 1,69 > 1,36.
Отсюда уровни ряда независимы.
3. Проверка соответствия ряда остатков нормальному закону распределения на основе RS-критерия.
RS= (Emax-Emin)/S= (7,149+ 9,159)/ 4,677= 3,487
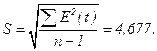
По таблице критические границы отношения R/S (Приложение 1) находим значение для n=30 и 5%-го уровня значимости интервал от 3.47 до 4.89
Для нашего случая
3.47<RS<4.89;
3.47<3,487<4.89;
т.е. гипотеза о нормальном распределении принимается.
4. Оценка точности модели
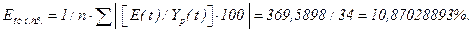
В связи с тем, что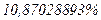 
< 11%, можно считать степень точности модели удовлетворяет неравенству
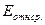< 11%.
5. Расчет прогнозных оценок.
В связи с выполнением всех условий проверки модели на адекватность для реального процесса можно осуществить прогнозирование данных на заданное число шагов вперед (Рис.4.).
Выберем значения k от k= 1 до k =14, в результате получим (смотри таблицу 9).
Таблиц 9.
Дата добавления: 2015-12-16; просмотров: 1607;