Определение z-преобразования выходного сигнала
Рассмотрим замкнутую импульсную систему, изображенную на рис. 19.4,а. Для этой системы справедливы следующие соотношения:
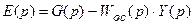 , (19.3)
, (19.3)
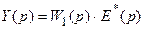 . (19.4)
. (19.4)
Подставив (19.3) в (19.4), получим
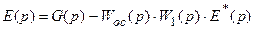 . (19.5)
. (19.5)
Перейдя к z-преобразованию в (19.5), будем иметь
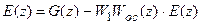 .
.
Отсюда может быть найдена z-передаточная функция замкнутой системы относительно ошибки
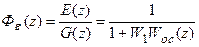 . (19.6)
. (19.6)
Теперь подвергнем z-преобразованию уравнение (19.4) и подставим в него выражение для E(z) из (19.6). В результате этого будет найдено z-преобразование выходного сигнала
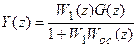 . (19.7)
. (19.7)
Из (19.7) находим z-передаточную функцию замкнутой системы по задающему воздействию
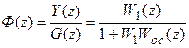 . (19.8)
. (19.8)
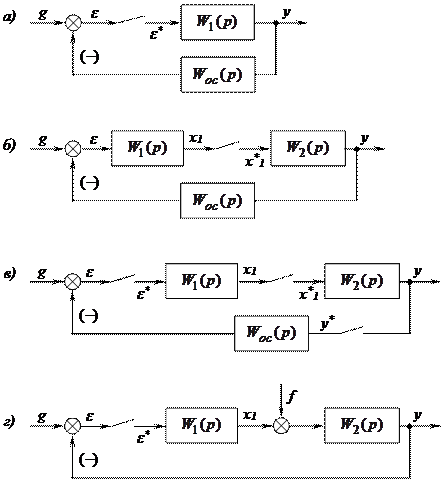 |
Рис. 19.4. Структурные схемы замкнутых импульсных САУ.
Для структурной схемы импульсной системы, показанной на рис. 19.4,б, можно записать:
 , (19.9)
, (19.9)
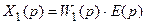 , (19.10)
, (19.10)
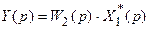 . (19.11)
. (19.11)
Подставляя (19.11) в (19.9), получаем
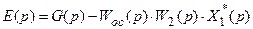 .
.
После этого исключим переменную E(p) из (19.10)
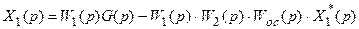 . (19.12)
. (19.12)
После z-преобразования уравнения (19.12) решим его относительно X1(z)
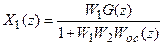 . (19.13)
. (19.13)
Далее, после z-преобразования (19.11), подставим в него (19.13) и найдем для выходного сигнала системы z-преобразование:
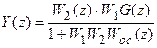 . (19.14)
. (19.14)
Поскольку входное воздействие в (19.14) входит в неявном виде, нельзя получить выражение для передаточной функции замкнутой системы.
Для импульсной системы, показанной на рис.19.4,в, можно записать:
 ,
,
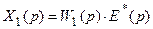 ,
,
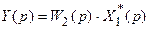 .
.
Подвергнув эти уравнения z-преобразованию и исключив переменные 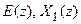 , получим выражение для выходного сигнала системы
, получим выражение для выходного сигнала системы
 . (19.15)
. (19.15)
После этого может быть найдена передаточная функция замкнутой системы
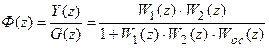 . (19.16)
. (19.16)
Определим теперь выражение для z-преобразования выходного сигнала импульсной системы (рис. 19.4,г) от возмущающего воздействия. Для этой системы имеем (g=0):
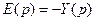 , (19.17)
, (19.17)
 , (19.18)
, (19.18)
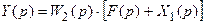 . (19.19)
. (19.19)
Из (19.17) и (19.18) получим
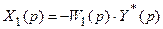 . (19.20)
. (19.20)
Подставив (19.20) в (19.19), получим
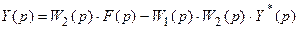
После z-преобразования этого уравнения найдем
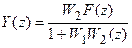 . (19.21)
. (19.21)
В это уравнение z-преобразование возмущающего воздействия входит в неявном виде, поэтому выражение для z-передаточной функции замкнутой системы по возмущению не может быть получено.
Дата добавления: 2015-12-11; просмотров: 570;
