Передаточные функции импульсных СУ
1. Уравнения и передаточные функции импульсных разомкнутых систем
Рассмотрим импульсную систему (рис. 19.1). По аналогии с интегралом сверки для непрерывных систем
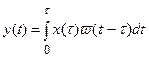
для импульсной системы можно записать
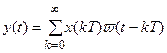 ,
,
где 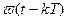 - импульсная переходная функция приведенной непрерывной части (или просто непрерывной части). Для решетчатой функции будем иметь
- импульсная переходная функция приведенной непрерывной части (или просто непрерывной части). Для решетчатой функции будем иметь
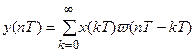 ,
,
а после z-преобразования этого выражения получаем
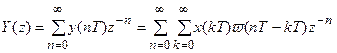 .
.
 |
Рис. 19.1. Разомкнутая импульсная САУ
Подстановка 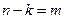 позволяет получить
позволяет получить
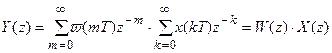 .
.
Отсюда имеем
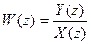 .
.
Это выражение по своей форме совпадает с выражением для передаточной функции непрерывной системы, только здесь рассматривается при нулевых начальных условиях отношение z-преобразований выходного Y(z) и входного сигналов X(z) дискретной системы.
Такую передаточную функцию называют z-передаточной функцией или импульсной передаточной функцией системы. Эта передаточная функция рассматривается только для дискретных сигналов, если же сигналы непрерывные, то фиксируются их значения только для дискретных моментов времени, кратных периоду прерывания сигнала в системе.
Выражение для z-передаточной функции может быть получено и по-другому – с использованием свойств идеального импульсного элемента.
Действительно, непрерывный сигнал на выходе системы (рис. 19.1) можно записать в виде
 .
.
Преобразуем по Лапласу это уравнение:
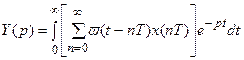 .
.
После замены  будем иметь
будем иметь
 .
.
Учитывая, что
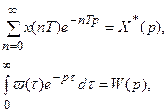
можно записать
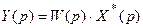 . (19.1)
. (19.1)
Полученное выражение (19.1) показывает, что если на входе непрерывной части действует дискретный сигнал x*(t), то изображение по Лапласу непрерывного выходного сигнала Y(p) будет определяться произведением передаточной функции непрерывной части W(p) на дискретное преобразование Лапласа от входного сигнала X*(p).
Далее находим выражение для дискретного преобразования выходного сигнала на основании свойства 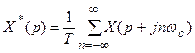 идеального импульсного элемента. Эта процедура равносильна установке дополнительного ключа на выходе рассматриваемой системы (рис. 19.2).
идеального импульсного элемента. Эта процедура равносильна установке дополнительного ключа на выходе рассматриваемой системы (рис. 19.2).
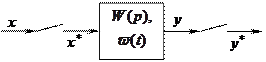 |
Рис. 19.2. Разомкнутая импульсная САУ с дискретным выходом.
Поэтому получаем
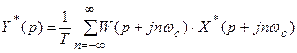 .
.
Поскольку функция  периодическая и выполняется условие
периодическая и выполняется условие  , можно записать
, можно записать
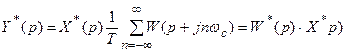 . (19.2)
. (19.2)
Таким образом, при дискретном преобразовании Лапласа произведения непрерывного преобразования Лапласа на дискретное преобразование Лапласа некоторых функций (19.1) получаем произведение дискретных преобразований этих функций (19.2). Полученное свойство дискретного преобразования Лапласа весьма упрощает процесс определения передаточных функций дискретных систем.
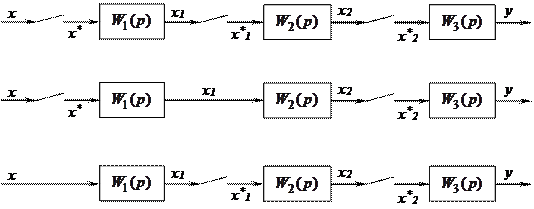
На рис. 19.3 показаны варианты структурных схем разомкнутых импульсных систем с различными числом и местами включения импульсных элементов. Требуется определить z-преобразованиевыходного сигнала систем и их передаточные функции.
 а)
а)
б)
в)
Рис. 19.3. Структурные схемы разомкнутых импульсных САУ.
Для системы (рис. 19.3,а) можно записать следующие уравнения:
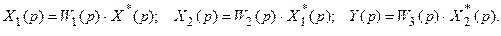
Подвергнув эти уравнения дискретному преобразованию Лапласа и исключив промежуточные переменные, находим связь между входным и выходным сигналами этой системы:
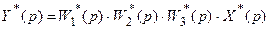 .
.
Для перехода к z-преобразованию делаем подстановку 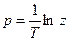 , поскольку
, поскольку  . В результате получаем
. В результате получаем
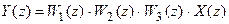 ,
,
а для z-передаточной функции имеем
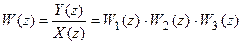 .
.
Для системы (рис. 19.3,б) справедливы следующие зависимости:
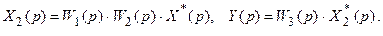
Рассмотрим первое из этих уравнений. Его можно записать  , где условно обозначим произведение непрерывных преобразований Лапласа
, где условно обозначим произведение непрерывных преобразований Лапласа 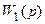 и
и 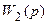 через
через 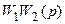 . Теперь найдем дискретное преобразование Лапласа
. Теперь найдем дискретное преобразование Лапласа
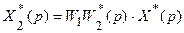 .
.
Следует иметь в виду, что 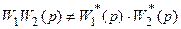 . Действительно,
. Действительно,
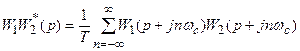 ,
,
а
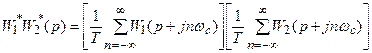 .
.
Далее получаем
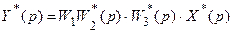 .
.
Путем подстановки 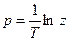 переходим к z-преобразованию
переходим к z-преобразованию
 ,
,
z-передаточная функция системы имеет вид
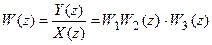 .
.
Рассмотрим систему, изображенную на рис. 19.3,в. Для нее можно записать следующие уравнения:
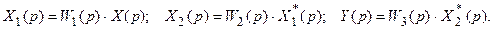
Из первого уравнения находим 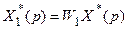 , далее получаем
, далее получаем

После подстановки 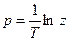 переходим к z-преобразованию:
переходим к z-преобразованию:
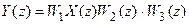 .
.
В это выражение z-преобразование входного сигнала входит в неявном виде, поэтому z-передаточная функция для такой системы не может быть получена.
Дата добавления: 2015-12-11; просмотров: 881;
