Математическая модель реального импульсного элемента.
На вход импульсного элемента подается непрерывная величина, а на выходе возникает последовательность импульсов, форма которых может быть различной: прямоугольной, треугольной, экспоненциальной и т.д.
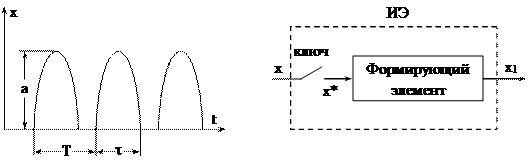 |
| Рис. 17.8. Последовательность импульсов | Рис. 17.9. Эквивалентная схема импульсного элемента |
На рис. 17.8 показана немодулированная последовательность импульсов. Основные параметры этой последовательности: амплитуда импульса а, период повторения Т, длительность импульса t=gT, где g - скважность импульсов, представляющая собой отношение длительности импульса t к периоду Т.
Импульсный элемент можно представить в виде двух последовательно соединенных элементов: простейшего или идеального импульсного элемента и формирующего элемента (рис.17.9). Идеальный импульсный элемент преобразует непрерывный входной сигнал x в последовательность мгновенных импульсов (d-функций) х*, площадь которых определяется значениями входного сигнала в соответствующие дискретные моменты времени, и изображается в виде ключа. Формирующий элемент представляет собой непрерывный фильтр, который преобразует мгновенные входные импульсы в импульсы заданной формы. Таким образом, форма импульсов реального импульсного элемента представляет собой импульсную переходную функцию формирующего элемента, поскольку на входе его действует последовательность d-функций х* (рис. 17.10).
 |
Рис. 17.10. Схема импульсной САУ с приведенной непрерывной частью
На основании рассмотренного схема с реальным импульсным элементом ИЭ и непрерывной частью (рис.17.10,а) может быть условно представлена в виде последовательного соединения идеального импульсного элемента (ключа) и приведенной непрерывной части, которая включает формирующий элемент и непрерывную часть системы (рис.17.10,б). Такой подход позволяет упростить исследование импульсных схем.
Математическая модель реального импульсного элемента. Рассмотрим свойства идеального импульсного элемента (рис. 17.9). Пусть x(t)– непрерывный входной сигнал, а x*(t) – дискретный выходной сигнал идеального импульсного элемента, который по определению выражается так:
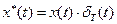 , (17.1)
, (17.1)
где 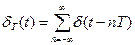 - последовательность единичных импульсов (d-функции) с периодом прерывания Т.
- последовательность единичных импульсов (d-функции) с периодом прерывания Т.
Представим 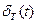 в виде комплексного ряда Фурье
в виде комплексного ряда Фурье
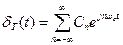 ,
,
где 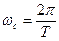 - частота прерывания,
- частота прерывания,  - коэффициент ряда Фурье, которые определяются так:
- коэффициент ряда Фурье, которые определяются так:
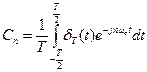 .
.
Поскольку 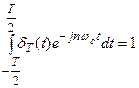 , то
, то 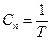 , и поэтому получаем
, и поэтому получаем
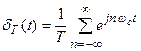 . (17.2)
. (17.2)
Подставляя (17.2) в (17.1), находим
 . (17.3)
. (17.3)
Преобразуем по Лапласу полученное уравнение (17.3), выражающее связь входного и выходного сигналов идеального импульсного элемента
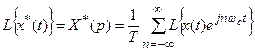 . (17.4)
. (17.4)
На основании теоремы смещения уравнение (17.4) принимает вид
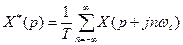 , (17.5)
, (17.5)
где Х(р) – преобразование Лапласа от непрерывного сигнала. Уравнение (17.5) позволяет выразить дискретное преобразование Лапласа Х*(р) через преобразование Лапласа от соответствующей непрерывной функции Х(р).
Функция 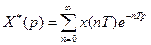 является периодической функцией с периодом повторения
является периодической функцией с периодом повторения 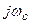 , поэтому
, поэтому
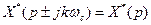 , (17.6)
, (17.6)
 где k – целое число.
где k – целое число.
 Рис. 17.11. Периодические свойства функции
Рис. 17.11. Периодические свойства функции 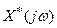
Рис. 17.12. Перекрытие частотных спектров
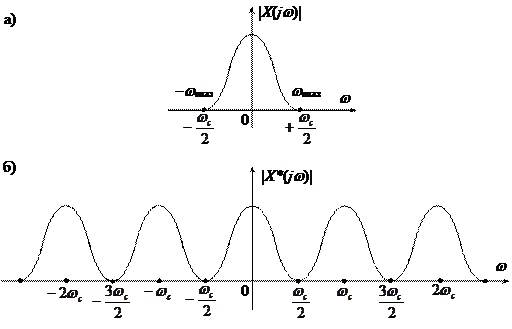
Периодические свойства 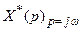 показаны на рис.17.11. Частотный спектр входного сигнала (рис.17.11,а) определяет в соответствии с (17.3), частотный спектр выходного сигнала идеального импульсного элемента (рис.17.11,б):
показаны на рис.17.11. Частотный спектр входного сигнала (рис.17.11,а) определяет в соответствии с (17.3), частотный спектр выходного сигнала идеального импульсного элемента (рис.17.11,б):
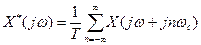 .
.
Выходной сигнал помимо основного спектра частот, совпадающего со спектром входного сигнала, содержит дополнительные спектры, сдвинутые на 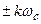 , где k – целое число. Амплитуда выходного сигнала, как это следует из (17.3), уменьшена по сравнению с амплитудой входного сигнала в
, где k – целое число. Амплитуда выходного сигнала, как это следует из (17.3), уменьшена по сравнению с амплитудой входного сигнала в 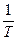 раз.
раз.
Очевидно, основная составляющая выходного сигнала, имеющая одинаковый частотный спектр со входным, полностью определяет входное воздействие. Эта основная составляющая может быть выделена с помощью специальных фильтров и дать полную информацию о входном сигнале только в том случае, если ее частотный спектр не перекрыт спектрами дополнительных составляющих. В противном случае основная составляющая будет нести искаженную информацию о входном воздействии (рис.17.12).Теорема Котельникова устанавливает условие неискаженной передачи информации импульсным элементом. Это условие заключается в том, чтобы частота прерывания импульсного элемента, по крайней мере вдвое превышала максимальную частоту частотного спектра входного сигнала wmax.
Передаточные функции формирующих элементов.Определим передаточные функции формирующих элементов для прямоугольной и треугольной форм импульсов.
Аналитически прямоугольный и треугольный импульсы могут быть выражены следующим образом (рис.17.13).
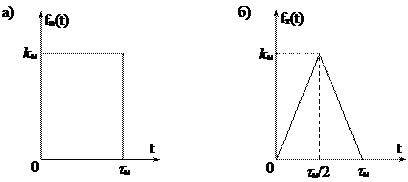 |
Рис. 17.13. Прямоугольный и треугольный импульсы
Прямоугольный импульс (рис.17.13,а)
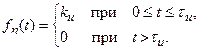 (17.7)
(17.7)
Треугольный импульс (рис.17.13,б)
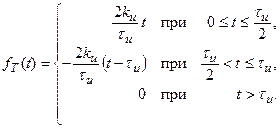 (17.8)
(17.8)
Для определения соответствующих передаточных функций преобразуем по Лапласу уравнения (17.7) и (17.8)
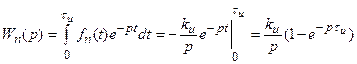 , (17.9)
, (17.9)
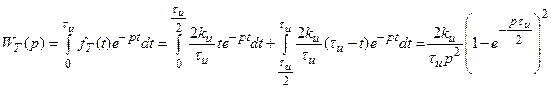 . (17.10)
. (17.10)
Выражения (17.9) и (17.10) представляют собой передаточные функции формирующих элементов при амплитудно-импульсной модуляции для прямоугольной и треугольной форм импульсов.
Дата добавления: 2015-12-11; просмотров: 2066;
