Структурные схемы дискретных систем

Рассмотрим схемы дискретных САУ. На рис.17.2 показана функциональная схема импульсной системы. Импульсный элемент (ИЭ) на этой схеме включен в цепь сигнала ошибки и преобразует непрерывный сигнал ошибки в определенную последовательность импульсов. Далее сигнал поступает на усилительно-преобразовательное устройство (УПУ), в котором формируется команда, управляющая исполнительным устройством (ИУ). Исполнительное устройство воздействует на объект управления (ОУ).

Рис. 17.2. Схема импульсной САУ

В импульсных системах период квантования может быть как постоянным, так и переменным. В любой импульсной САУ может быть выделена непрерывная часть, к которой относятся некоторые звенья регулятора и объект управления, имеющие непрерывные характеристики.

В общем случае импульсная система может содержать несколько импульсных элементов, которые включаются в соответствующих точках схемы.

Функциональная схема цифровой системы (рис.17.3) включает в себя:

- преобразователь непрерывных величин в дискретный код (Н-Д), представляющий собой устройство ввода;

- цифровую вычислительную машину (ЦВМ), которая осуществляет вычисления в соответствии с заданным алгоритмом управления;

- преобразователь дискретного кода в непрерывный сигнал (Д-Н), являющийся выходным преобразователем;

- непрерывную часть (НЧ), в которую обычно входят объект управления, исполнительные и другие устройства, имеющие непрерывные характеристики.

Рис. 17.3. Схема цифровой САУ

На рис. 17.4 показана функциональная схема многомерной цифровой системы. Многомерный объект управления этой системы имеет n выходных координат 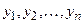для управления которыми требуется формирование n соответствующих управляющих воздействий.

Рис. 17.4. Функциональная схема многомерной цифровой системы

Следует отметить, что присущий цифровым системам эффект квантования по уровню делает их существенно нелинейными, что в значительной степени затрудняет их исследование. Кроме этого, процесс вычисления алгоритма управления связан с затратой определенного времени, что приводит к запаздыванию формирования необходимого управления по отношению к текущему времени.

Однако при построении математической модели цифровой системы используют ряд упрощающих допущений. Считают, что поступление информации на ЦВМ и выдача управляющих сигналов производятся периодически синхронно и синфазно. Это допущение оправдано в том случае, если время, затрачиваемое на ввод и выдачу данных, мало по сравнению с периодом работы системы. Кроме этого, полагают, что эффектом квантования сигналов по уровню можно пренебречь, поскольку количество разрядов преобразователей в ЦВМ достаточно велико. Все это позволяет перейти от цифровой системы к некоторой эквивалентной импульсной системе с привлечением математического аппарата исследования импульсных систем.

На рис. 17.5 показана функциональная схема импульсной системы, которая эквивалентна цифровой системе. Здесь импульсные элементы (ИЭ₁, ИЭ₂, ¼, ИЭ_n) определяют дискретный характер входных сигналов ЦВМ, дискретный фильтр (ДФ) характеризует процесс формирования управляющих сигналов, экстраполяторы (Э₁, Э₂, ¼, Э_n) отображают процесс преобразования дискретных значений управляющего сигнала в непрерывный сигнал. Таким образом, характерной особенностью импульсных систем, эквивалентных цифровым, является наличие дискретных фильтров и экстраполяторов.

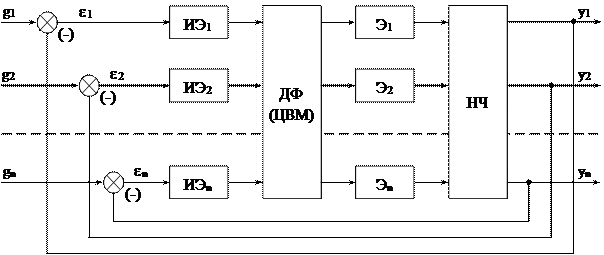Рис. 17.5. Функциональная схема эквивалентной импульсной системы

К достоинствам дискретных систем автоматического управления относятся:

1) возможность использования высокоточных измерительных устройств малой мощности за счет кратковременного подключения их в работу;

2) использование отдельных устройств регуляторов для работы с несколькими каналами за счет разделения по времени работы этих каналов;

3) повышение помехоустойчивости цифровых систем за счет использования квантования сигнала не только по времени, но и по уровню;

4) возможность реализации на ЦВМ сложных вычислительных алгоритмов для формирования управлений и простота их перенастройки.