Сложение векторов и умножение на число.
В каждом классе векторов (например, перемещений, скоростей, сил, напряженности магнитного поля) можно определить операции, известные, как сложение векторов и умножение их на число.
Сложение производится либо, используя правило параллелограмма, либо – веревочного многоугольника.
Произведением вектора 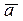 на число
на число 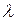 называется вектор
называется вектор 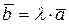 , определяемый следующими условиями:
, определяемый следующими условиями:
1). 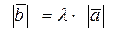
2). 
3). Векторы 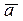 и
и 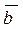 одинаково направлены, если
одинаково направлены, если 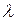 >0, и противоположно - если
>0, и противоположно - если 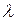 <0.
<0.
| Векторы образуют линейное пространство |
1).  .
.
2).  .
.
3). 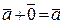 , где 0 - нулевой вектор.
, где 0 - нулевой вектор.
4).  , где
, где 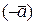 - противоположный вектор, 0- нулевой.
- противоположный вектор, 0- нулевой.
5). 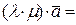 , где
, где 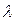 ,
, 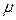 - числа.
- числа. 
6).  .
.
7). 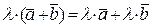 .
.
8). 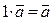 .
.
| Сложение векторов и умножение вектора на число со свойствами 1– 8 называются линейными операциями над векторами. |
Рассмотрим векторы на оси. Осью называется прямая на которой выбрано положительное направление. Численным значением вектора 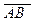 на оси называется число равное длине вектора, взятой со знаком плюс, если направление вектора совпадает с направлением оси, и со знаком минус, если оно противоположно направлению оси. Величина вектора
на оси называется число равное длине вектора, взятой со знаком плюс, если направление вектора совпадает с направлением оси, и со знаком минус, если оно противоположно направлению оси. Величина вектора 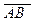 обозначается
обозначается 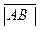 .
.
Пример.Пусть длина вектора | 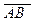 |=|
|=| 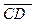 |=5 . Найти величины этих векторов, если они расположены на оси l, как показано на рисунке 1.2.
|=5 . Найти величины этих векторов, если они расположены на оси l, как показано на рисунке 1.2.
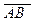 = 5,
= 5, 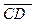 =–5.
=–5.
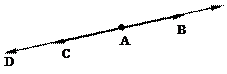
Рис. 1.2
Очевидно, что величина суммы двух и большего числа векторов на оси равна алгебраической сумме величин слагаемых векторов.
Пример.Найти величину суммы векторов 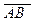 и
и 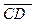 на оси, (рис.1.3) если |
на оси, (рис.1.3) если | 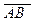 |=3, |
|=3, | 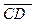 |=5 .
|=5 .
Решение.
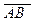 +
+ 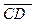 =3 + (–5)= –2.
=3 + (–5)= –2.
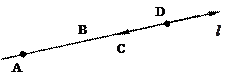
Рис. 1.3
Имеет место утверждение: при любом расположении трех точек на оси величины векторов 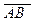 ,
, 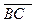 и
и 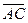 удовлетворяют соотношению
удовлетворяют соотношению 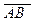 +
+ 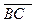 =
= 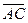 (основное тождество).
(основное тождество).
Доказательство представлено на рис. 1.4, где показаны всевозможные случаи расположения трех точек A, B, C на оси l.
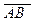 +
+ 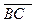 =
= 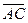
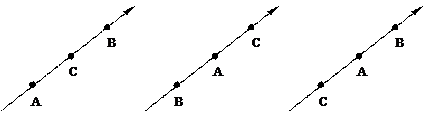 |
Рис. 1.4

Проекция вектора
Проекцией вектора 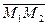 на заданную ось lназывается численное значение вектора
на заданную ось lназывается численное значение вектора  на оси l (рис. 1.5а).
на оси l (рис. 1.5а).
Проекцией вектора 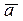 на вектор
на вектор  называется проекция вектора
называется проекция вектора 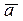 на ось, имеющую с вектором
на ось, имеющую с вектором 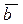 одинаковое направление (рис. 1.5б).
одинаковое направление (рис. 1.5б).
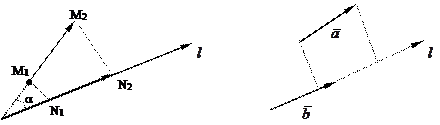
Рис. 1.5а Рис. 1.5б
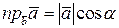 , где
, где  - угол между вектором
- угол между вектором 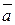 и осью l.
и осью l.
Свойство проекций:
1) Проекция суммы векторов на ось равна сумме проекций этих векторов, т.е.
Пр. 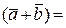 Пр.
Пр. 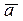 + Пр.
+ Пр. 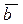 ;
;
2) проекция произведения вектора 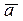 на число
на число 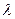 равна произведению числа на проекцию вектора
равна произведению числа на проекцию вектора 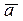 , т.е. Прl
, т.е. Прl 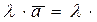 Прl
Прl 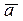 .
.
Дата добавления: 2015-12-10; просмотров: 1055;
