Применение теории массового обслуживания для описания деятельности человека-оператора

Деятельность оператора в ряде случаев может быть описана с позиций теории массового обслуживания. Если представить поступление сигналов к человеку-оператору как некоторые требования, вынуждающие его работать в соответствии с некоторыми правилами, инструкциями, то можно сказать, что оператор -обслуживает эти требования. Следовательно, деятельность оператора можно представить как процесс обслуживания.

Применение теории массового обслуживания позволяет решить многие вопросы организации деятельности человека-оператора. К их числу относится определение необходимого числа операторов, определение требований к уровню подготовленности ^оператора (обученности, скорости реакций, объему памяти и т. д.), определение допустимой плотности потока сигналов, поступающих к оператору, решение некоторых задач организации взаимодействия операторов. Представляется возможность вычисления .вероятностей различных состояний системы «человек-машина», jb том числе и различных нежелательных состояний. Следовательно, так же, как и теория информации, теория массового обслуживания дает количественные методы описания деятельности человека-оператора.

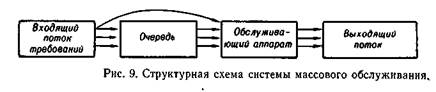
Наиболее общая схема системы массового обслуживания показана на рис. 9. Требования на обслуживание образуют входящий поток. Как правило, этот поток является случайным, т. е. требования могут поступать в случайные моменты времени. Входящий поток задается законом распределения. Обычно считается, что такой поток подчинен закону Пуассона:

ф (2.19)

где P_k (τ) — вероятность появления k требований за промежуток

времени τ;

λ — параметр потока, среднее количество требований,

поступающих в единицу времени.

Как следует из формулы (2.19), для задания входящего потока, подчиненного закону Пуассона, нужно определить лишь

одну величину — среднее число требований (заявок), поступающих в единицу времени. Эта величина иначе называется плотностью входящего потока. При дальнейших рассуждениях предполагается, что входящий поток подчинен закону Пуассона. Такой поток называют также простейшим.

Заявки, поступившие в момент занятости обслуживающего аппарата, становятся в очередь на обслуживание./В зависимости от организации очереди системы массового обслуживания могут быть различных типов: с отказами, с ожиданием (без потерь), с ограничениями. В системе с отказами заявка, поступившая в момент занятости обслуживающего аппарата, в очередь не становится и к обслуживанию не принимается, т. е. теряется, получает отказ. В системе с ожиданием заявки могут находиться в очереди неограниченно долго и никогда не теряются. В системе с ограничениями заявки могут становиться в очередь, но находиться там лишь некоторое время, по истечении которого они теряются (система с ограниченным ожиданием).

При проектировании деятельности оператора следует стремиться, если это возможно, к тому, чтобы эта деятельность была организована по 'схеме обслуживания с неограниченным ожиданием. При этом вся поступающая информация будет принята к: обслуживанию.

Основной характеристикой обслуживающего аппарата является длительность обслуживания. Как правило, это случайная величина, описываемая экспоненциальным законом распределения,

ф (2.20)

где Р (τ) — вероятность того, что время обслуживания превосходит величину t;

μ, — интенсивность обслуживания, или среднее количество требований, обслуживаемых в единицу времени;

τ_обсл = 1/μ ¾ среднее значение времени обслуживания.

В рамках теории массового обслуживания человек-оператор представляется обслуживающим аппаратом системы массового обслуживания (СМО). Поток сигналов (команд), поступающих к оператору, представляется как входящий поток заявок, а время обработки этих сигналов или реализации команд — как время обслуживания. Заявки, поступившие в течении времени, когда оператор занят обслуживанием предыдущих заявок, становятся в очередь и обслуживаются только после освобождения обслуживающего аппарата.

Применение аппарата теории массового обслуживания позволяет учесть и ряд специфических особенностей, характерных для деятельности оператора и обусловленных представлением его в качестве обслуживающего аппарата. Так, например, ограниченность объема оперативной памяти заставляет рассматривать СМО с ограниченной длиной очереди, а ограниченность длительности сохранения информации в памяти — СМО с ограниченным временем ожидания. Групповая деятельность операторов может быть учтена при рассмотрении многоканальных или многофазных СМО в зависимости от вида взаимодействия операторов.

Возможность совершения ошибок оператором и их исправления приводит к необходимости рассмотрения СМО с ненадежным обслуживающим аппаратом. При этом ошибки оператора рассматриваются как поток отказов обслуживающего аппарата, а время их исправления — как время восстановления.

При простейшем входящем потоке и показательном законе распределения времени обслуживания могут быть получены аналитические зависимости вероятностных характеристик времени ожидания и длины очереди от параметров входящего потока и обслуживающего аппарата (человека-оператора). Последние могут быть заданы в зависимости от уровня обученности и подготовленности оператора.

Так, например, если деятельность оператора организована таким образом, что требования не могут покинуть систему необслуженными, следует рассматривать СМО с ожиданием. Основные характеристики такой одноканальной системы следующие [74].

Вероятность того, что оператор не занят обслуживанием поступившей информации

ф(2.21)

Вероятность того, что длина очереди равна k,

P_k = ρ^k(1—ρ). (2.22)

Вероятность того, что время ожидания в очереди превышает некоторую величину τ_доп,

ф(2.23)

Вывод указанных формул можно найти в литературе по теории массового обслуживания, например [74]. Аналогичные формулы могут быть получены и для других типов СМО. Эти формулы широко используются при проверке выполнения предельно допустимых норм деятельности оператора. Пример их использования рассматривается в гл. X.

К сожалению, применение методов теории массового обслуживания связано с введением целого ряда ограничений относительно вида входящего потока, закона распределения времени обслуживания. Более полное решение задачи возможно методом статистического моделирования, который не накладывает принципиально никаких ограничений на указанные характеристики СМО.