Основные положения теории информации и применение их в инженерной психологии

Применение теории информации основано на отождествлении человека-оператора, передающего информацию со средств отображения на органы управления, с каналом связи. Такое отождествление правомерно, поскольку в теории связи любое устройство, осуществляющее передачу информации на расстояние, называется каналом связи. Следовательно, и человек-оператор, выполняющий функции передачи информации, представляет собой специфический канал связи, называемый иногда человеческим каналом. Теоретической базой для исследования каналов связи является теория информации.

Теорией информации называется наука, изучающая количественные закономерности, связанные с получением, обработкой, хранением и передачей информации. Под информацией в инженерной психологии принято понимать любые изменения в управляемом процессе, отображаемые средствами представления информации или непосредственно воспринимаемые оператором, а также команды, указания о необходимости осуществления тех или иных воздействий на процесс [И]. Всякое сообщение информативно, если оно представляет то, чего мы не знали до этого сообщения.

Любое сообщение представляет собой совокупность сведений о некоторой физической системе. Применительно к деятельности оператора сообщение — это совокупность зрительных, акустических и иных сигналов, воспринятых в данный момент, а также «сигналов», хранимых в памяти оператора. Сообщение приобретает смысл (содержит определенное количество информации) только тогда, когда состояние системы заранее неизвестно, случайно, т. е. системе заранее присуща какая-то степень неопределенности.

В качестве меры неопределенности физической системы X, принимающей состояния Xi (i = 1, 2, .. ., n), используется понятие энтропии

ф(2.1)

где Pi — вероятность i-го состояния системы.

Энтропия системы, как это следует из (2.1), тем больше, чем больше общее число различных состояний, и чем меньше отличаются друг от друга вероятности этих состояний. При равновероятном появлении различных состояний (Р = 1/n) максимальна:

ф(2.2)

Неопределенность системы уменьшается при получении каких-либо сведений об этой системе. Чем больше объем полученных сведений, чем они более содержательные, тем большей информацией о системе можно располагать. Поэтому естественно количество информации измерять уменьшением энтропии той системы, для уточнения состояния которой предназначены эти сведения.

Если априорная (исходная) энтропия системы была Н(Х), а после получения сведений об этой системе (например, после обновления информации на устройствах отображения) энтропия стала Н₀(Х), то количество полученной при этом информации

I_х = H(X)-H₀(X). (2.3)

В том практически важном случае, когда в результате полученных сведений состояние системы стало полностью определенным, т. е. H₀(X) = 0, количество полученной информации равняется энтропии системы:

I_x = Н(Х). (2.4)

В выражениях (2.1) и (2.2) логарифм можно брать по любому основанию. В теории информации принято пользоваться двоичными логарифмами. При этом энтропия и количество информации измеряются в двоичных единицах информации, или битах. Бит — это энтропия простейшей системы, имеющей два равновероятных состояния.

Применение теории информации в инженерной психологии обусловлено влиянием на деятельность человека неопределенности (энтропии) процессов и объектов управления. Ценность теоретико-информационного подхода в том, что он позволяет исследовать влияние на деятельность человека не только тех

событий, которые произошли, но главным образом тех, которые могли бы произойти, т. е. влияние априорных возможностей на настоящую и будущую деятельность человека. При этом количество информации, преобразуемой человеком, характеризует степень сложности решаемой им задачи.

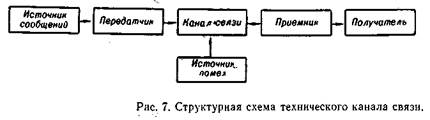
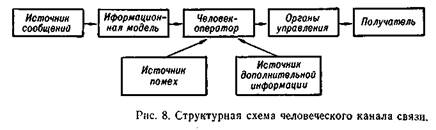
Рассмотрим основные аналогии между техническим (рис. 7) и человеческим (рис, 8) каналами связи. Источник сообщений является источником информации, передаваемой по каналу связи. Передатчик преобразует сообщение в сигнал, который способен передаваться по каналу связи. Приемник преобразует полученный сигнал и восстанавливает по нему переданное сообщение. Сигнал при передаче по каналу связи может подвергаться воздействию помех.

При передаче по человеческому каналу связи передатчиком является информационная модель, преобразующая поступающие от машины сообщения о состоянии процессов и объектов управления в сигналы, которые может воспринять оператор. Эти сигналы передаются оператором на органы управления, выполняющие роль приемника и преобразующие их в сообщения, которые могут быть «поняты» машиной.

Количество информации, переданной по человеческому каналу, может существенно отличаться от количества поступившей информации (энтропии источника информации). Это отличие обусловлено, во-первых, тем, что, как идля технического канала, часть информации может быть потеряна за счет воздействия помех. Во-вторых, количество информации увеличивается за счет использования дополнительной информации. Эта информация образуется за счет привлечения некоторых данных, хранимых в памяти оператора, а также в том случае, если оператору для осуществления требуемых воздействий на органы управления необходимо проделать какие-то вычисления, проверить некоторые логические условия или осуществить запоминание некоторой части информации. Общее количество информации, передаваемой по человеческому каналу связи,

I_ч = Н(Х)+Н_доп- Н_пом, (2.5)

где Н(Х) — энтропия источника сообщений, или количество информации, получаемой оператором от информационной модели;

Н_доп —дополнительное количество информации, используемой оператором в процессе решения задачи;

Н_пом —энтропия источника помех, под влиянием которых искажается часть поступившей информации. Эти помехи вызываются как внешними, так и внутренними, психофизиологическими факторами.

Энтропия источника сообщений оценивается по формулам (2.1) или (2.2). При пользовании этими формулами следует иметь в виду, что они оценивают энтропию взаимно независимых сообщений. Иными словами, предполагается, что появление того или иного сообщения не изменяет вероятность появления следующего сообщения.

При работе оператора в СЧМ такой случай не всегда возможен. Как правило, предъявляемая последовательность сигналов обладает логической избыточностью. Это означает, что появление

определенного сигнала изменяет вероятность появления следующего сигнала. Наличие логической избыточности равносильно уменьшению энтропии, поскольку появление определенного сигнала х, уменьшает неопределенность очередного состояния информационной модели.

При подсчете количества поступающей информации в этом случае необходимо пользоваться формулами условной энтропии. Так, например, энтропия второго и третьего порядка равна:

ф(2.6)

ф(2.7)

где Р_ij и P_ijk — вероятности появления всех возможных диаграмм и триграмм сигналов (совместного появления двух и трех сигналов),

Н₁ —энтропия первого порядка, определяемая по формуле (2.1);

A_n², A_n²—максимально возможное число диаграмм и триграмм сигналов, равное числу размещений по два и по три из общего числа п сигналов.

Формула (2.6) выражает среднюю энтропию сигнала при условии, что уже известен предыдущий, формула (2.7) — энтропию сигнала, если известны два предыдущих. Подобным способом можно вычислить и энтропию более высоких порядков.

Формулы (2.1) и (2.2) используют для подсчета количества информации, получаемой при выборе одного сигнала из последовательности в п сигналов. Помимо этого, на основе энтропийного анализа можно оценить сложность работы с приборами, расположенными на информационной модели (считывание показаний, установка заданных значений). Энтропия сообщения от прибора определяется выражением [64]

ф(2.8)

где х_тax, x_тin — максимальное и минимальное значения шкалы

прибора;

δ — абсолютная погрешность считывания показаний

сприбора.

Очень часто приходится определять общую информацию, получаемую оператором от k различных индикаторов. Если каждый из них индицирует наступление независимых событий, то общее количество информации равно:

ф(2.9)

где H_i —энтропия i-го индикатора;

k — общее число индикаторов.

Дополнительная информация, передаваемая по человеческому каналу связи, может быть трех видов: 1) информация, подлежащая запоминанию; 2) информация, используемая при вычислениях и проверке логических условий; 3) информация, извлекаемая из памяти.

Информация, подлежащая запоминанию, может быть также трех видов. Если запоминанию подлежит m символов (знаков, сигналов) из общего числа k символов, то количество запоминаемой информации

H_зап = Iog₂k^m= m Iog₂k. (2.10)

Если же от оператора не требуется запоминать порядок наступления сигналов, а необходимо запомнить только сами сигналы, то количество информации будет меньше:

ф(2.11)

В тех случаях, когда совокупность сигналов заранее известна» но неизвестен порядок их следования, количество информации во всей последовательности равно:

H_зап = Iog₂m = Iog₂k. (2.12)

Формулы (2.10) — (2.12) выражают суммарное количество информации во всей последовательности. Для получения количества информации на один символ величину H_зап необходимо уменьшить в m раз:

ф(2.13)

Количество информации, используемое при осуществлении в уме простейших вычислительных операций (сложение, умножение, деление и т. д.), равно [64]:

ф(2.14)

где H_i — максимальные значения используемых при вычислении

чисел;

R — максимально возможное значение результата вычисления;

k — количество чисел, используемых для получения R. Например, при сложении трех чисел k = 3, при делении одного числа на другое k = 2.

При проверке логических условий количество информации

ф(2.15)

где l —число проверяемых логических условий;

n_i — число возможных альтернатив (исходов), возникающих при проверке i-го условия.

Извлечение информации из памяти осуществляется всякий раз, когда нужно принять решение по реализации принятой информации. В этом случае оператор должен вспомнить, какое действие необходимо осуществить в ответ на появление данного сигнала. Количество информации при этом равно:

ф(2. 16)

где P_i —вероятность осуществления i-го действия

r — общее число различных действий, которые может выполнять оператор;

Q — число одновременно выполняемых действий из г возможных (Q≤r). Если, например, оператору в ответ на появление некоторого сигнала нужно нажать 3 кнопки из 16 возможных, то r = 16, Q = 3;

P_i — вероятность использования (нажатия) каждой из 16

кнопок.

Таким образом, определены все составляющие дополнительной информации, передаваемой по человеческому каналу связи:

H_доп = H_зап+H_выч+H_лог+H_пам

Теоретико-информационные модели деятельности оператора применяются при решении ряда практических задач. Во-первых, количество передаваемой человеком информации является мерой сложности работы оператора. Следовательно, таким способом можно сравнивать между собой различные виды деятельности. Во-вторых, зная количество информации, можно оценить время, которое оператор затрачивает на переработку этой информации, поскольку между ними, как правило, существует линейная зависимость. Подробнее об этом сказано в гл. X. В-третьих, знание количества информации позволяет согласовать темп выдачи информации (производительность источника сообщений) с психофизиологическими возможностями человека по ее приему и обработке, иными словами — с пропускной способностью оператора.

Применение методов теории информации в практике инженерно-психологических исследований связано с рядом трудностей, основные из которых следующие.

1. До конца не раскрыты способы формирования оператором алфавита (совокупности) сигналов. Принято считать, что этот алфавит совпадает с физическим алфавитом сигналов, что не всегда имеет место. В процессе переработки информации человек может укрупнять информацию, производить перекодирование, использовать прошлый опыт и т. д., т. е. пользоваться алфавитом, отличающимся от входного алфавита сигналов. 48

2. Субъективные вероятности появления того или иного состояния системы могут отличаться от объективных. Например, для необученного оператора все состояния равновероятны, для полностью обученного оператора, хорошо усвоившего статистическую природу сигналов, субъективные вероятности близки к объективным.

3. Теория информации не учитывает смысловую сторону ин формации. На деятельность же человека оказывает влияние не только неопределенность (вероятность) поступления сигнала но и его смысл.

4. В теории информации рассматриваются только стационарные процессы, статистические характеристики которых не меняются с течением времени. Свойства же человека не остаются неизменными: они меняются по мере обучаемости, утомления, воздействия помех и т. д.

5. Различные виды информации, с точки зрения влияния на работу оператора, не равноценны, поэтому при оценке сложности работы оператора необходимо учитывать их различный «вес», различное влияние на одни и те же характеристики оператора.

Наличие этих ограничений приводит на практике к тому, что рассчитанное количество информации не всегда совпадет с действительно переработанным человеком. Вследствие этого возможны расхождения между теоретическими результатами и практическими данными. Поэтому информационные методы дают лишь приближенное решение перечисленных выше задач. Тем не менее эти методы находят широкое применение в инженерной психологии, потому что в ряде случаев только они могут дать количественную оценку сложности работы оператора. Это относится главным образом к ситуациям, в которых человеку приходится выбирать один вариант из нескольких возможных.

Дальнейшее развитие информационных методов применительно к анализу и описанию работы оператора идет по пути совершенствования существующих методов, использующих энтропийные оценки количества информации. Так, например, в работе [58] существенно расширяется понятие энтропии по сравнению со случаями, рассмотренными выше.

Вполне понятно, что любой сигнал индикатора как источника информации может полезно служить задачам контроля и управления лишь в том случае, если он будет соотнесен ко времени его появления и экспозиции. Таким образом, для деятельности оператора важна не только статистическая (частота появления), но и временная (время появления) неопределенность. В силу этого возникает необходимость явного введения времени в исходные соотношения для оценки энтропии и количества информации. С математической точки зрения этот шаг эквивалентен переходу от уровня случайных событий на уровень случайных процессов в моделировании взаимодействия человека и машины. С позиций же инженерной психологии это является применением процессуального подхода к решению поставленных задач.

При таком подходе в качестве основы для формирования выражений энтропии и информации необходимо рассматривать вероятности наступления тех или иных событий x_i в интересующий нас момент t на отрезке времени наблюдения 0 ≤t≤ Т, т. е. вероятности P(x_i, t). Тогда для полной количественной характеристики неопределенности ситуаций с учетом неопределенности, вносимой фактором времени, будем иметь

ф (2.17)

Среднее количество информации в сообщении, вырабатываемом на отрезке времени наблюдения, составит

ф (2.18)

Нахождение вероятностей Р(х_i, t) является специфической .-задачей и определяется типом и характером протекания процесса -управления, а также теми требованиями, которые предъявляются к деятельности оператора.