Обработка результатов инженерно-психологического эксперимента
Многие характеристики деятельности оператора (время решения задачи, число ошибок, физиологические показатели и др.) являются случайными величинами, изменяющими свое значение от опыта к опыту. Случайность этих характеристик обусловлена как различием между отдельными операторами, так и подверженностью влиянию на них огромного числа факторов объективного и субъективного характера. Поэтому обработку результатов эксперимента (как реального, так и машинного) необходимо вести статистическими методами, достаточно хорошо разработанными в математической статистике.
Основными задачами статистической обработки результатов инженерно-психологического эксперимента являются: оценка параметров искомых характеристик, сравнение этих параметров, построение эмпирических зависимостей.
Основными параметрами случайных величин (характеристик деятельности оператора) являются математическое ожидание, дисперсия и вероятность наступления того или иного события. Предположим, проведено N измерений какой-то характеристики деятельности оператора, например, времени решения определенной задачи. В результате этого получено N значений этой характеристики х1, x2, ..., xn. Тогда математическое ожидание х и дисперсия D (х) величины х равны:
ф(2.27)
Математическое ожидание характеризует среднее значение случайной величины, дисперсия является мерой рассеивания (разброса) случайной величины вокруг своего среднего значения. В практических случаях чаще используется корень квадратный от дисперсии, называемый средним квадратическим отклонением S = 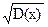 и имеющий ту же размерность, что и сама случайная величина.
и имеющий ту же размерность, что и сама случайная величина.
Оценкой для вероятности появления какого-либо события служит относительная частота
p(x) = 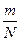 (2.28)
(2.28)
где т — число случаев, в которых данное событие имеет место. Статистическая оценка случайных величин необходима потому, что полученные параметры (2.27), (2.28) сами являются случайными величинами, зависят от числа опытов. Поэтому когда нужно сравнить две случайные величины, следует помнить, что полученное между ними различие может быть случайным и не всегда означает, что эти величины различны на самом деле. Проверку этого факта следует вести с помощью статистических критериев. Наиболее часто приходится сравнивать между собой средние значения. Различие между двумя математическими ожиданиями 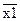 и
и 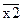 значимо, т. е. не случайно, если выполняется условие
значимо, т. е. не случайно, если выполняется условие
ф(2.29)
где t1-p— случайная переменная, подчинена распределению Стьюдента с f = N1 + N2 — 2 степенями свободы;
N1 , N2 — число опытов, по результатам которых вычислены параметры 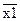 и
и 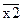 ;
;
р — уровень значимости;
D (х) — средневзвешенная дисперсия, равная:
ф(2.30)
Уровень значимости р показывает вероятность ошибки при проверке гипотезы о равенстве средних значений. Одним из широко применяемых на практике уровней значимости является р = 0,05. Это означает, что при проверке гипотез о равенстве средних в 5% случаев мы можем допустить ошибку, приняв полученное расхождение неслучайным (значимым). В табл. 1 приводятся значения величины t0,95 для различных f.
Таблица 1
| f | ∞ | ||||||||||
| 0,95 | 6,21 | 2,35 | 2,02 | 1,90 | 1,86 | 1,81 | 1,75 | 1,73 | 1,70 | 1,67 | 1,64 |
В практике проведения инженерно-психологического эксперимента часто возникает задача сравнения дисперсией двух случайных величин. Различие между двумя дисперсиями S12 и S22 считается значимым, если выполняется условие
ф(2.31)
где F1-р— значение случайной переменной, подчиненной распределению Фишера с f1 и f2 степенями свободы (f1 = N1-1), (f2= N2-1)
При пользовании формулой (2. 31) необходимо иметь в виду, что индекс 1 всегда относится к большей дисперсии, а индекс 2 — к меньшей.
Значения величины F для уровня значимости p=0,05 приведены в табл. 2.
Таблица 2
| f1 | f2 | ||||||||
| 1 | r | ∞ | |||||||
| 10,1 | 9,6 | 9,3 | 9,1 | 9,0 | 8,9 | 8,7 | 8,6 | 8,5 | |
| 7,7 | 6,9 | 6,6 | 6,4 | 6,3 | 6,2 | 5,9' | 5,8 | 5,6 | |
| 6,0 | 5,1 | 4,8 | 4,5 | 4,4 | 4,3 | 4,0 | 3,8 | 3,7 | |
| 5,3 | 4,5 | 4,1 | 3,8 | 3,7 | 3,6 | 3,3 | 3,1 | 2,9 | |
| 5,0 | 4,1 | 3,7 | 3,5 | 3,3 | 3,2 | 2,9 | 2,7 | 2,5 | |
| 4,4 | 3,5 | 3,1 | 2,9 | 2,7 | 2,6 | 2,3 | 2,1 | 1,8 | |
| 4,2 | 3,3 | 2,9 | 2,7 | 2,5 | 2,4 | 2,1 | 1,9 | 1,6 | |
| 4,0 | 3,2 | 2,8 | 2,5 | 2,4 | 2,3 | 1,9 | 1,7 | 1.4 | |
| ∞ | 3,8 | 3,0 | 2,6 | 2,4 | 2,2 | 2,1 | 1,8 | 1,5 | 1,0 |
При проведении инженерно-психологического эксперимента возможен случай, когда один или несколько факторов начинают определенным или случайным образом изменяться. Для оценки степени влияния этого фактора на деятельность оператора используют дисперсионный анализ. Целью этого анализа является изучение влияния переменных факторов на генеральное среднее (математическое ожидание) исследуемой характеристики деятельности оператора.
Рассмотрим основные положения методики однофакторного дисперсионного анализа. Имеется k уровней изменения некоторого фактора А (А1,А2, ..., Ak). На каждом уровне зафиксировано N значений измеряемой величины х. Эти значения сведены в табл. 3.
Таблица 3
| Номер наблюдения | Значение измеряемой величины х на уровне фактора | |||||
| A1 | A2 | …. | Ai | …. | Ak | |
| x11 x12 | x21 x22 | … ... | х1i x2i | … ... | x1k x1k | |
| . . j . | . . xj1 . | . . xj2 . | . . … . | . . xji . | . . … . | . . xjk . |
| . N | . xN 1 | . xN 2 | . .... | . xN i | . .... | . xN k |
| ¯xi | ¯x1 | ¯x2 | .... | ¯xi | .... | ¯xk |
| S12 | S12 | S22 | .... | Si2 | …. | Sk2 |
Среднее значение и дисперсия измеряемой величины на i-м уровне изменения.фактора
ф (2.32)
Очевидно, дисперсия Si2 характеризует влияние случайных факторов на i-м уровне изменения исследуемого фактора A. Если между дисперсиями Si2 нет значимых различий (это различие проверяется по формуле (2.31)), то их можно использовать для оценки генеральной дисперсии
ф(2.34)
где ¯х - среднее всех kN наблюдений, равное:
ф(2.35)
Дисперсия SА2 имеет f = k – 1степеней свободы. Для того чтобы влияние фактора А было значимым, необходимо и достаточно, чтобы дисперсия SА2 значимо отличалась от S02. Это различие значимо, если
ф(2.36)
где F1-p — распределение, которое имеет f1 = k — 1 и f2 = k(N—1) степеней свободы.
Если результаты дисперсионного анализа показывают значимость влияния фактора Л, в некоторых случаях бывает необходимо определить, какие средние различны. Эту оценку можно провести с помощью критерия Стьюдента.
ГЛАВА III
Дата добавления: 2015-12-10; просмотров: 995;
