Влияние структуры на эффективность групповой деятельности

Эффективность решения групповых задач существенным образом зависит от структуры группы, т. е. от характера соединений операторов. Пример изображения структуры малой группы в виде графа показан на рис. 34. Здесь окружностями, являющимися узлами графа, показаны операторы, а линиями — взаимосвязи между ними. Считается, что каждая линия, соединяющая два узла, одинакова с остальными и представляет единицу расстояния. Расстоянием d^ между двумя узлами i и / называется наименьшее число звеньев, по которым можно пройти от одного узла к другому. Так, например, в графе, изображенном на рис. 34 б, d₁₇ = 3, d₆₃ = 4, d₆₇ = 6.

Каждый i-й узел графа характеризуется своими показателями центральности [24]

ф(8.2)

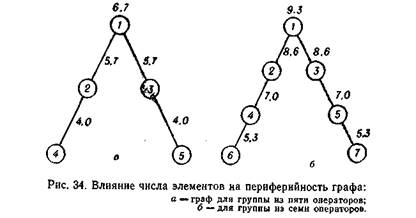
Введенный показатель центральности обладает тем недостатком, что добавление новых узлов к графу, не меняя позиции узла с максимальной центральностью, меняет в то же время численное значение показателя центральности этого узла (например, узел / на рис. 34, а и рис. 34, б). Чтобы избежать этого, вводится понятие относительной периферийности узла

П_i = С_max —С_i(8.3)

и полной периферийности графа

П = ∑П_i,. (8.4)

Понятие относительной периферийности хорошо совпадает с нашими интуитивными представлениями о позиции того или иного узла. Центральный узел в этом случае всегда имеет П_i=0.

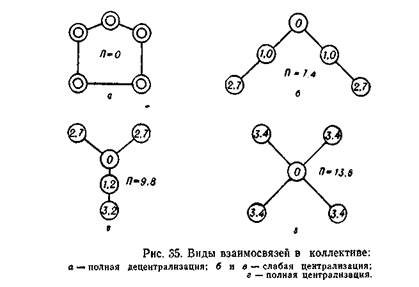
Обнаружено, что показатель периферийности П определяет в ряде случаев эффективность решения групповых задач. Так, например, при решении ряда задач наименьшее время и наименьшее количество ошибок наблюдаются при соединении операторов по схеме рис. 35, г. В то же время наихудшие показатели имеет структура 35, а, соответствующая полной децентрализации (автономности) работы операторов [11].

К сожалению, сравнение эффективности решения групповых задач с помощью показателя П возможно только для графов,

имеющих одинаковое число узлов, например, таких, какие показаны на рис. 35. В то же время сравнение графов с разным числом узлов с помощью этого показателя не имеет смысла, поскольку его численное значение зависит от числа узлов. В этом можно убедиться, сравнив, например, рис. 34, а и рис. 34, б. В таких случаях более эффективным показателем для сравнения различных структур является общее число ребер (взаимосвязей) графа. Проведенные исследования показали, что способность к решению групповых задач при небольших значениях

коэффициента взаимного влияния определяется исключительно количеством ребер в графе, а не его характером. Эта способность оказывается обратно пропорциональной общему. числу связей (ребер) графа.

Эффективность решения групповых задач зависит также и от степени взаимодействия операторов. Чем сильнее степень взаимного влияния операторов на результат совместной работы, тем менее эффективна деятельность группы. Степень взаимодействия операторов оценивается коэффициентом взаимного влияния, показывающим, во сколько раз деятельность оператора оказывает большее влияние на результат работы партнера, чем на собственный результат. Экспериментально установлено, что для одного и того же вида групповой деятельности [26]

k_допN = const, (8.5)

где k_доп — допустимый коэффициент взаимного влияния операторов, N — общее число ребер графа.

При k > k_доп групповая задача становится неразрешимой. Такие задачи требуют распределения функциональных обязанностей в группе, выделения лидера, т. е. человека, взявшего на себя роль организатора решения групповой задачи. Остальные операторы выполняют роль ведомых, т. е. действуют под руководством лидера. Экспериментально установлено, что наибольшая способность к лидерству обнаруживается у тех операторов, показатель периферийности которых имеет минимальное значение. Этим также подтверждается тот факт, что группы с централизованной структурой имеют лучшую способность к решению сложных групповых задач.

Кроме этого, лидер должен обладать и некоторыми необходимыми субъективными качествами, выделяющими его из всей группы. К таким качествам относятся: хорошее знание решаемой задачи, авторитетность, способность организовать ведомых на решение задачи, т. е. повести их за собой и т. д. Следовательно, для выполнения роли лидера необходимо наличие объективных (центральное положение в группе) и субъективных (личные качества) условий. Несоблюдение этих условий приводит к принижению роли лидера, к ухудшению способности группы решать совместные задачи.

Следует также отметить, что в тех случаях, когда выбор лидера заранее не планируется, роль лидера складывается стихийно, наилучшие способности к решению групповых задач обнаруживаются у групп с децентрализованной структурой (например, рис. 35, а). Это объясняется тем, что условия для выявления лидера одинаковы для всех операторов. В то же время для групп с централизованной структурой (рис. 35, г) вероятность обнаружения лидера в узле с наименьшей периферийностью значительно меньше, чем в однородном графе.

Имеющиеся в настоящее время данные по групповой психологии, несмотря на их ограниченный характер, позволяют сформулировать некоторые принципы инженерно-психологического проектирования групповой деятельности операторов. На основании проведенного распределения функций между человеком и машиной определяются задачи, решаемые операторами. Исходя из возможной структуры процесса управления и рассмотренных особенностей групповой деятельности выбирается приемлемая структура группы. При выборе структуры следует стремиться к уменьшению общего показателя периферийности и числа ребер структурного графа. Однако при этом следует учесть психологические возможности операторов по приему и обработке информации, ибо стремление к упрощению структуры группы может привести к недопустимой информационной нагрузке, приходящейся на одного оператора. Кроме того, необходимо также проверить величину коэффициентов взаимного влияния и обеспечить повышение неравенства k < &_доп. В заключение определяется положение лидера и ведомых в группе и формулируются основные требования к ним. В некоторых случаях для повышения надежности и быстродействия работы операторов может быть применено дублирование (резервирование) их работы.