Оценка динамической устойчивости.

Динамическую устойчивость простейшей электрической системы с автоматическим регулятором пропорционального типа, в которой генератор работает на шины неизменного напряжения, необходимо рассматривать с учетом нелинейности характеристик ее элементов.

Смену режимов работы можно проанализировать на основе метода последовательных интервалов с линеаризацией уравнений переходных процессов на каждом интервале. Оценку устойчивости в этом случае выполняют по характеру изменения угла перемещения ротора генератора во времени.

Устройство форсировки возбуждения в самом простом варианте реализует закорачивание сопротивления в цепи ОВВ генератора при снижении напряжения на его зажимах до значения 0,85U_г.ном.. При этом ток в цепи ОВВ и пропорциональное ему напряжение возбудителя с учетом времени запаздывания t_зап от срабатывания устройств АРВ (порядка 0,05 с) возрастают до наибольшего значения Е_qe.maxпо экспоненциальному закону с постоянной времени возбудителя Т_е (рис.34).

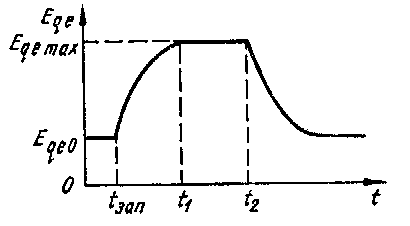
Рис.34. Характер изменения э. д. с. генератора при форсировке его возбуждения

Так как э. д. с. в установившемся режиме генератора E_qe0пропорциональна, а в относительных единицах равна напряжению возбудителя, то при форсировке возбуждения закон ее нарастания можно записать в виде

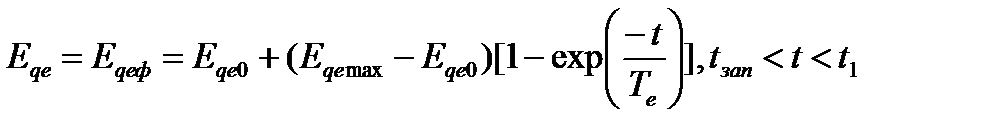(70,а)

Форсировка возбуждения продолжается до достижения напряжения генератора (0,95÷1,05)U_г.ном . При снятии форсировки напряжение возбудителя и э. д. с. генератора уменьшаются по закону

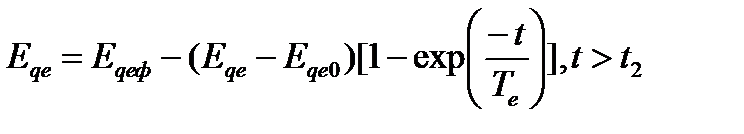(70,б)

где

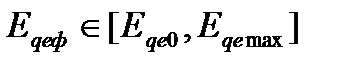
Зная закон изменения э. д. с. генератора E_qe(t), можно методом последовательных интервалов численно решить уравнение электромагнитного переходного процесса в роторе генератора

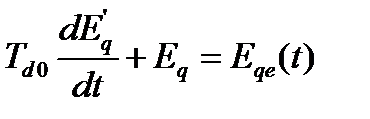
совместно с численным решением уравнений его относительного движения (67.1)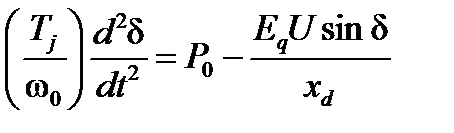

в различных режимах. Приращение продольной переходной э. д. с. за расчетный интервал времени определяется выражением

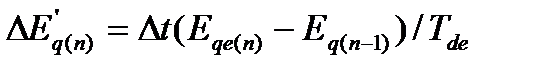(71)

В конце интервала 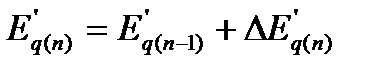(72)

В момент возникновения аварийного состояния (КЗ) продольная переходная э. д. с. не изменяется, т. е, E'_q0= E'_q(0)'. Это условие и является исходным при определении изменения по интервалам э. д. с.E_q'. В нормальном режиме

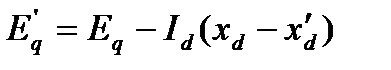(73,а)

где продольная составляющая тока генератора вычисляется через внутреннюю реактивную мощность генератора и значение синхронной э. д. с.E_q.

Порядок расчета динамической устойчивости простейшей электрической системы с автоматическим регулятором пропорционального типа с использованием зависимости δ(t):

1. Составляют схемы замещения сети для нормального, аварийного и послеаварийного режимов и определяют собственные, а также взаимные проводимости и сопротивления.

2. На основании расчета нормального режима устанавливают значения P₀, δ₀, E_q0, E'_q0.

3. Do заданным характеристикам регулятора и возбудителя строят кривую изменения э. д. с. E_q0(t)для установившегося режима при форсировке возбуждения генератора.

4. Вычисляют значение э. д. с. E_q(0) для первого момента после возникновения аварийного состояния (КЗ). Расчетная формула при этом имеет вид

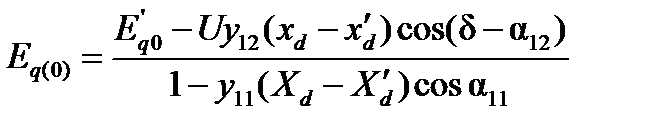
5. Используя (71), находят приращение переходной э. д. с. в течение первого интервала времени:

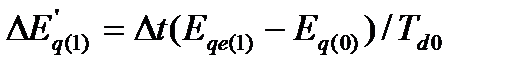
где E_qe(1) - среднее значение E_qeза первый интервал времени.

6. По формуле (72) рассчитывают значение переходной э. д. с. в конце первого (начале второго) интервала времени:

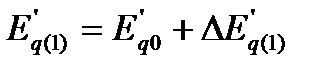
7. Определяют активную мощность, отдаваемую генератором о начале первого интервала времени,

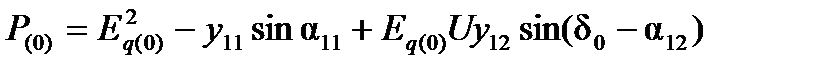
и избыток мощности за этот интервал

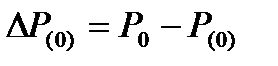
8. Вычисляют приращение угла перемещения ротора генератора за первый интервал времени:

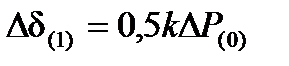
Для каждого из последующих интервалов времени расчет повторяют по последним пяти пунктам. Если при этом в n-м интервале времени угловая характеристика мощности генератора не меняется, то приращение угла

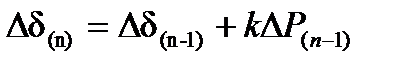
а если меняется, то

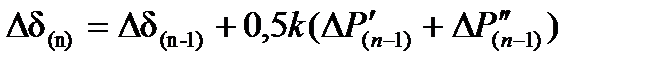
Для каждого интервала времени рассчитывают напряжение генератора с использованием предварительно найденного по формуле значения синхронной э. д. с. По вычисленным значениям напряжения генератора контролируют момент снятия форсировки его возбуждения.

При расчете устойчивости электрической системы, генераторы которой оснащены обычными возбудителями, приближенно можно считать, что форсировка возбуждения генераторов продолжается до достижения углом δ максимального значения.

Учет автоматического регулятора сильного действия при оценке устойчивости системы связан с анализом характеристических уравнений более высоких порядков, чем при учете автоматического регулятора пропорционального типа.

Введение в закон регулирования возбуждения производных изменения параметров режима обеспечивает расширение области устойчивости до еще больших значений угла δ, чем при автоматическом регуляторе пропорционального типа, вплоть до его предельного значения. При этом существенно увеличивается и передаваемая в сеть предельная мощность (см. рис. 32,в, кривая 3).

С помощью автоматического регулятора сильного действия исключается влияние собственного сопротивления генератора на устойчивость системы.

Таким образом, наличие разных пределов передаваемой в сеть мощности при использовании того или иного устройства АРВ генератора позволяет по-разному представлять генератор в схеме замещения при расчете устойчивости электрической системы:

генератор без АРВ замещают синхронной продольной э. д. с. E'_q=const за синхронным индуктивным сопротивлением x_d(рис.35, а);

Рис. 35. Схемы замещения генератора с упрощенным учетом его АРВ по внутреннему пределу мощности

генератор с автоматическим регулятором пропорционального типа может быть замещен источником э. д. с. E'_q=const за переходным индуктивным сопротивлением x'_d(рис. 35.б);

генератор с автоматическим регулятором сильного действия, обеспечивающим стабилизацию напряжения на зажимах генератора, является источником неизменного напряжения U_г=const, которое считают независимым параметром режима (рис. 35, в).