Оценка статической устойчивости.
Рассмотрим простейшую электрическую систему с генератором, оснащенным автоматическим регулятором пропорционального типа по отклонению напряжения и работающим на шины с неизменным напряжением (рис.33, а).
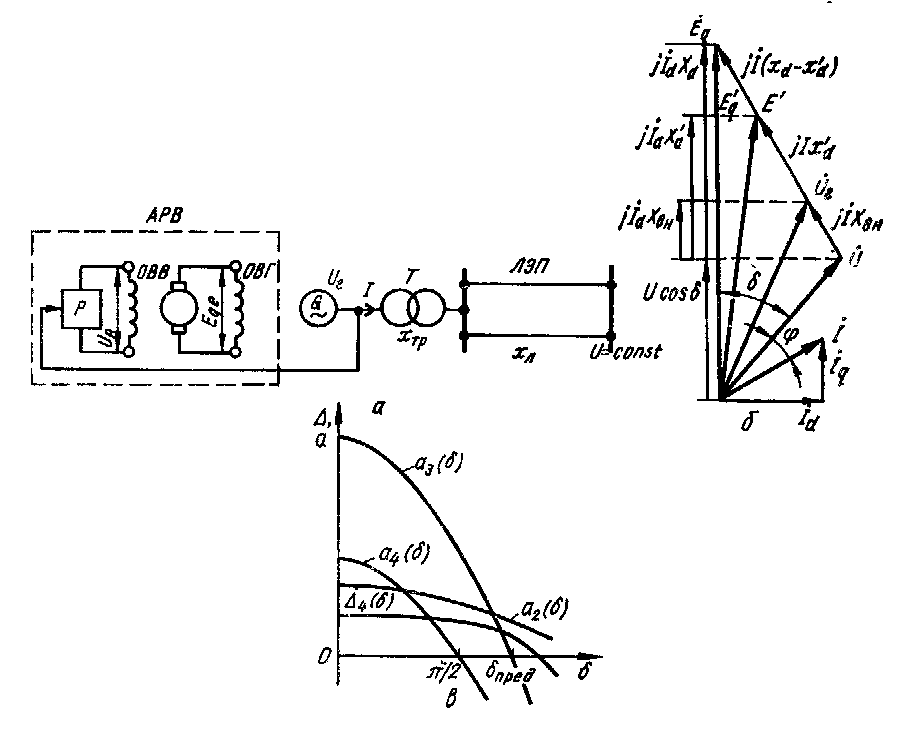
Рис. 33. К анализу статической устойчивости электрической системы с автоматическим регулятором пропорционального типа по отклонению напряжения
Переходный процесс можно описать системой уравнений, включающей в себя:
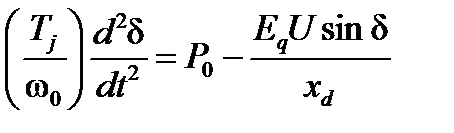 уравнение относительного движения ротора генератора
уравнение относительного движения ротора генератора
 уравнение переходного процесса в роторе генератора
уравнение переходного процесса в роторе генератора
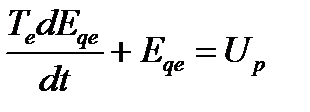 уравнение переходного процесса в цепи возбуждения возбудителя
уравнение переходного процесса в цепи возбуждения возбудителя
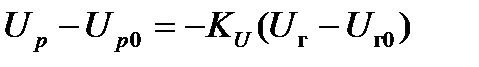 уравнение идеального автоматического регулятора напряжения пропорционального типа, мгновенно изменяющего напряжение на обмотке возбуждения возбудителя, пропорционально отклонению напряжения на зажимах генератора.
уравнение идеального автоматического регулятора напряжения пропорционального типа, мгновенно изменяющего напряжение на обмотке возбуждения возбудителя, пропорционально отклонению напряжения на зажимах генератора.
где 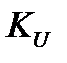 -коэффициент усиления (регулирования) регулятора.
-коэффициент усиления (регулирования) регулятора.
Дополнительные уравнения, связывающие систему уравнений между собой, могут быть получены из векторной диаграммы генератора (рис.33,б):



 (67)
(67)
Если систему уравнений (67) представить в операторной форме, то можно вывести характеристическое уравнение:
 (68)
(68)
Где
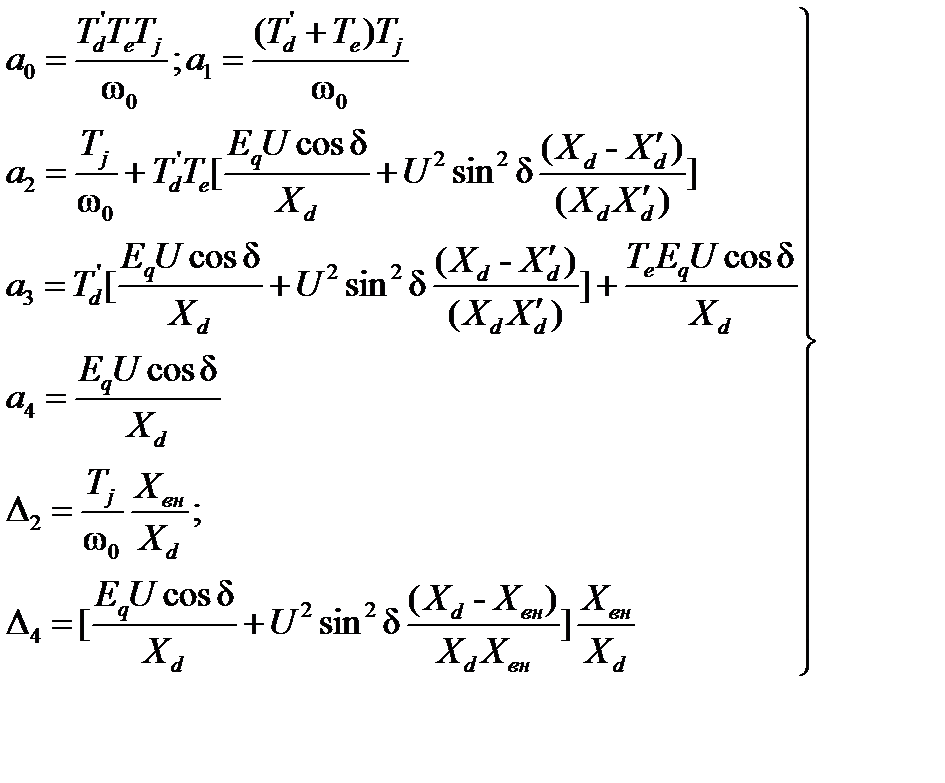 (69)
(69)
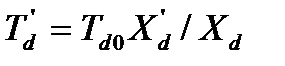 .
.
Анализируя (69), можно сделать следующие выводы:
коэффициенты а0и а1всегда положительны и не зависят от режима работы и параметров сети, на которую работает генератор;
коэффициенты а2, а3, Δ4 и а4 зависят от режима работы и параметров сети. С увеличением угла δ некоторые из них становятся отрицательными (рис.33,в), что свидетельствует о нарушении необходимого условия устойчивости системы, соответствующего положительным значениям всех коэффициентов характеристического уравнения.
Для выявления условий устойчивости системы можно воспользоваться критерием Гурвица:
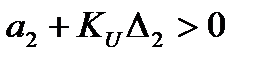
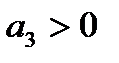

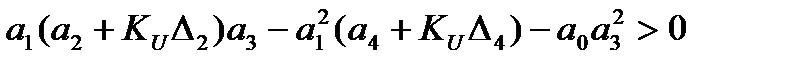
С целью упрощения анализа условий устойчивости вначале полагают, что постоянная времени возбудителя Те=0. Это позволяет получить характеристическое уравнение более низкого (до третьего) порядка, так как а0=0 см.(68).
При учете только электромагнитных переходных процессов в обмотке возбуждения устойчивость нерегулируемого генератора определяется граничным условием - положительным значением синхронизируемой мощности SEq=a4 определяемой при постоянстве э. д. с. Eq.
Анализ устойчивости системы с автоматическим регулятором пропорционального типа показывает, что действие АРВ генератора позволяет расширить область статической устойчивости системы за предел δ=π/2, причем граница устойчивости находится в пределах, соответствующих SEq=0 и SE’q=0.
Дата добавления: 2015-12-08; просмотров: 1173;
