Анализ производительности протоколов

1. Протокол с остановками и ожиданием.

Рассмотрим следующую систему (рис. 5.21).

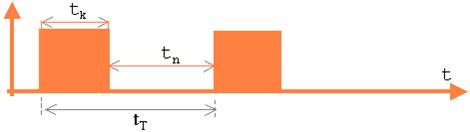
Рис. 5.21. Передача кадра при анализе производительности протокола с остановками и ожиданием.

Предположим, что вероятность ошибочного приема в пункте В равна р. Тогда очевидно, что при отсутствии ограничений на число повторных передач среднее время правильной передачи найдется в виде:

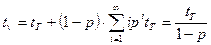(5.1)

Это выражение показывает что для того чтобы случилось i-тое повторение, кадр должен быть доставлен с ошибкой i раз. Вероятность правильного приема при i-м повторении в точности равна (1-р).

В случае насыщения величина t_v представляет собой среднее время между правильно переданными кадрами. Максимальная производительность в доставленных пакетах является обратной величиной t_v, или

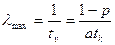(5.2)

где параметр a = t_Т/t_k >=1 вводится, чтобы связать производительность с длиной кадра данных.

Если теперь принять 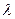равной практической интенсивности поступления кадров в передатчик, мы получим нормированную производительность для протокола с остановками и ожиданием в виде:

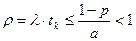(5.3)

2. Протокол с N- возвращениями (см. рис. 5.22 ).

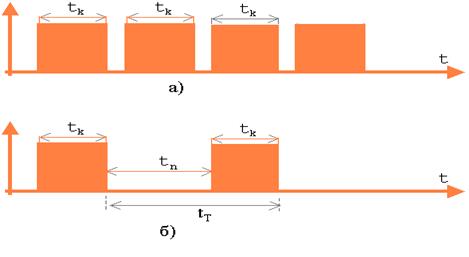
Рис. 5.22. Анализ системы с N-возвращениями: (а) безошибочная передача, (б) случай появления ошибки (сбоя)

Поскольку по схеме с N -возвращениями кадры могут передаваться непрерывно один за другим, минимальное время между передачами равно t_k, т.е. времени передачи кадра. Соответственно увеличивается максимальная производительность. Среднее время передачи кадра равно:

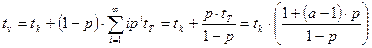(5.4)

Максимально возможная производительность получается в виде:

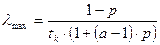(5.5)

Нормированная производительность для любой интенсивности поступления кадров ограничивается значением

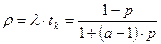(5.6)

Пример:

Пусть а = 4, р = 0.01. Тогда для протокола с остановками и ожиданием нормированная производительность ограничивается значением 0.99/4, тогда как соответствующая граница для схемы с N-возвращениями находится около 0.99/(1+0.01*3)=0.96. Т.е. схема с N-возвращениями превосходит схему с остановками и ожиданием в 4 раза. При а<1 предпочтительнее стратегия непрерывной передачи.