Методы случайного доступа к сети

Двумя основными способами доступа к общей среде передачи являются управляемый доступ с применением опроса и случайный доступ. В свою очередь существуют различные типы стратегий случайного доступа.

Методы случайного доступа полностью децентрализованы. Пользователь может передавать когда угодно, лишь с незначительными ограничениями, зависящими от метода доступа.

Из-за случайности моментов времени, в которые пользователи могут решить начать передачу, независимо от метода не исключена возможность того, что два или несколько пользователей могут выйти на связь в пересекающиеся промежутки времени. Это приводит к столкновениям (коллизиям), которые сначала должны быть распознаны, а затем разрешены. При увеличении нагрузки увеличивается и вероятность коллизий, что приводит к возможной неустойчивости работы рассматриваемых механизмов.

В результате производительность ограничивается некоторым максимальным значением, меньшим пропускной способности канала, и это значение в каждом случае зависит от первоначального механизма доступа и алгоритма разрешения коллизий.

Методы Алоха

Сначала методы случайного доступа были предложены для случаев, когда большое число пользователей пытаются довольно редко передать пачки сообщений или, когда друг с другом связываются небольшое число ЭВМ. Но применимо к производственным процессам, которые требуют строгого управления задержкой доступа, более предпочтителен управляемый доступ. Рассмотрим два простейших типа стратегии случайного доступа: чистую Алоху и синхроннуюАлоху [43].

Чистая Алоха

Эта схема сначала была применена для доступа к общему каналу сотрудниками Гавайского университета в начале 1970-х годов. По этой схеме пользователь, желающий передать сообщение, делает это когда угодно. В результате могут наложится во времени два или несколько сообщений, вызвав столкновение (коллизию).

Распознавание коллизий и сообщение о них пострадавшим пользователям в первоначальной системе Алоха направлялись по радио на центральный пункт. Также это могло осуществляться путем применения положительгых подтверждений в сочетании с перерывом. При обнаружении столкновения пострадавшие станции предпринимают попытки повторной передачи потерянного сообщения, но они должны распределять время попыток случайным образом, следуя некоторому алгоритму столкновения нового конфликта.

Стратегия доступа типа Чистой Алохи позволяет добиться производительности самое большее 1/2e » 0,18 пропускной способности канала. Введем сначала некоторые определения. За доступ к каналу состязаются N станций. Станция передает, в среднем, l пакетов в секунду (интенсивность обращений к сети). Величина 1/m представляет собой пропускную способность канала (m) в передаваемых пакетах в секунду. Рассмотрим теперь частный случай, при котором все передаваемые сообщения (пакеты) имеют среднюю длину t, соответствующую m единицам времени передачи. Будем считать, что интенсивность нагрузки S (эквивалентно r -нормированной по mнагрузке) характеризует использование канала вновь поступающими пакетами

S º r = Nlm

Величина 1/t, которая обозначается m, представляет собой пропускную способность канала в передаваемых пакетах в секунду. Таким образом, Nl/m = Nlm - относительное использование канала, или производительность, нормированная относительно каждого компьютера одинакова. Общая интенсивность пакетов, передаваемых в канал, включая вновь генерируемые и передаваемые повторно, имеет некоторое значение l’ > l (из-за коллизий от каждого компьютера будет передаваться больше сообщений из-за необxодимости возобновлять поток). Тогда фактическая интенсивность нагрузки, или использование канала, является параметром G, который равен

G = Nl’t.

Рассмотрим типичное сообщение длительностью t с, показанное на рис. 5.24.

Ошибка! Ошибка связи.

Рис. 5.24. Столкновение двух сообщений

Оно подвергается столкновению с другим сообщением, если эти два сообщения будут наложены одно на другое в любой точке. Легко заметить, передвигая пунктирное сообщение во времени, что столкновение может произойти в промежутке времени продолжительностью 2t с. Вероятность того, что в промежутке 2t с не произойдет столкновения, равна e^-2Nl’m=e^-2G.

Отношение S/G представляет долю сообщений из числа передаваемых в канал, которые проходят успешно. Это число должно быть равно вероятности отсутствия столкновений. Таким образом уравнение производительности для чистой Алохи:

S = Ge^-2G (5.11).

Здесь S - нормированная производительность (средняя скорость поступления пакетов, деленная на максимальную производительность 1/m), а G - нормированная пропущенная нагрузка. Таким образом, S – независимая переменная, а G - ее функция. График зависимости G от S имеет вид двузначной кривой (рис. 5.25).

Ошибка! Ошибка связи.

Рис. 5.25. Характеристика производительности; чистая Алоха

Отметим, что S имеет максимум S = 0,5e^-1» 0,18 при G = 0.5. Судя по формуле (4.11) или кривой при малой поступающей нагрузке S столкновения происходят редко, и G » S. Когда S начинает расти, приближаясь к максимальному значению 0.18, число столкновений быстро увеличивается, что ведет в свою очередь к росту вероятности столкновения. Система теряет устойчивость, S падает, а G увеличивается до больших значений.

Синхронная Алоха

Максимально возможная производительность схемы чистой Алохи может быть удвоена с помощью простого приема пазметки шкалы времени и разрешения пользователям начинать попытки передачи сообщений только в начале каждого временного интервала m (равного длительности сообщения). Эта схема требует, чтобы работа всех пользователей системы была синхронизирована во времени. Пример работы такой системы показан на рис. 5.26, на котором одно сообщение передано успешно, а с другим произошло столкновение.

Ошибка! Ошибка связи.

Рис. 5.26. Передача при синхронной Алохе

Поскольку сообщения могут быть переданы только в размеченные промежутки времени, столкновения происходят лишь когда одна или несколько попыток передачи совершаются в том же промежутке.

Вероятность успешной передачи задается в виде e^-G, а производительность для синхронной Алохи имеет вид

S = Ge^-G.

Нормированная производительность S достигает максимального значения 1/e » 0,368 при G = 1. Зависимость пропущенной нагрузки от производительности для синхронной Алохи показана на рис. 5.27, где она сравнивается с соответствующей зависимостью для чистой Алохи.

Из приведенной характеристики очевидно, что ввиду двух возможных значений G при заданной производительности S, для этой системы доступа также характерна неустойчивость.

Ошибка! Ошибка связи.

Рис. 5.27. Характеристика производительности; синхронная Алоха

5.8.5.2.Случайный доступ типа МДПН/ОС (CSMA/CD)

Протокол МДПН/ОС основан на методе чистой Алохи и позволяет улучшить ее характеристики. Метод МДПН/ОС входит в протокол сети Ethernet и принят, как один из стандартных методов в локальных сетях. Реализация локальных сетей по образцу сети Ethernet распространена весьма широко.

Основная концепция протокола МДПН/ОС очень проста . Все станции прослушивают передачу по линии. Станция, желающая передать сообщение, выходит на связь только после обнаружения свободного состояния канала. Эта процедура называется проверкой несущей, а стратегия, основанная на такой проверке, схемой многостанционного доступа с проверкой несущей (МДПН). Очевидно, что столкновения все же могут возникнуть, поскольку станции физически разнесены одна от другой, и две или несколько станций могут обнаружить свободное состояние канала и начать передавать, что и вызовет столкновение. Если станции обнаруживают столкновение (обнаружение столкновения - ОС), они передают всем остальным станциям специальный сигнал о помехе и отменяют свои передачи. Возможность проверки несущей позволяет увеличить производительность канала по сравнению с чистой Алохой, а обнаружение столкновения с прекращением передачи, вместо его завершения дает еще большее повышение производительности.

Был предложен и проанализирован ряд методов МДПН. Они различаются тем, как происходит управление передачей, если канал оказался занятым. Например, в схеме с p-настойчивостью станция, обнаружившая занятый канал, осуществляет передачу после того, как канал станет свободным, с вероятностью p. С вероятностью (1-p) передача откладывается на промежуток времени t распространения сигнала. При схеме с 1- настойчивостью станция осуществляет попытку передачи, как только канал окажется свободным. При ненастойчивой схеме станция переносит передачу на другое время в соответствии с предписанным распределением задержек передачи, проверяет несущую в это время и продолжает процесс.

Эти схемы применимы прежде всего в локальных сетях или в более крупных сетях, работающих со сравнительно небольшими скоростями передачи.

Протокол МДПН/ОС, работающий по правилу 1-настойчивости с добавлением возможности обнаружения столкновений в целях дальнейшего улучшения характеристик принят в качестве протокола в схеме Ethernet. Если обнаруживается столкновение и передача прекращается, попытка повторной передачи принимается через случайный промежуток времени, как и в схемах Алоха. Этот случайный промежуток времени удваивается каждый раз после обнаружения нового столкновения до некоторой максимальной величины, при которой станция выходит из строя и извещают вышестоящие уровни о нарушении связи. Это удвоение промежутка называется процедурой двоичного замедления и может улучшить характеристику системы.

Получим результаты анализа системы с дискретным временем, чтобы выявить характеристики задержек протокола МДПН/ОС.

Рассмотрим шинную структуру.

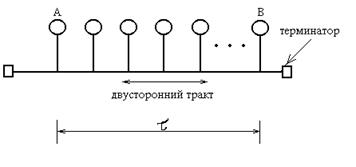
Рис. 5.28. Модель МДПН/ОС

Станции подключаются через пассивные ответвления к двусторонней шине. Сосредоточим внимание на двух наиболее удаленных станциях (А и В). Рассчитаем среднее время, требуемое для успешного запуска сообщения в шину. Обратная величина этого времени и будет максимальной производительностью. Назовем время до успешного завершения передачи сообщения виртуальным временем передачи t_v. Это время имеет три составляющие( см. рис. 5.29). Оно включает время m, требуемое для передачи сообщения, время t, требуемое для проверки завершения передачи, и время, кратное 2t единицам, для разрешения столкновений, если они обнаруживаются.

Пусть возникло столкновение между сигналами, передаваемыми станциями А и В. В худшем случае обнаружение столкновения займет на станциях А и В время в 2t с, после чего передача будет немедленно выключена. Это показано на рисунке 4.27 : станция А начинает передачу в некоторый момент времени. Перед тем, как сообщение станции А поступит на станцию В, последняя решает начать передачу. Станция В проверяет канал, находит его свободным и начинает собственную передачу. Это очевидное столкновение, которое обнаружится только через t c.

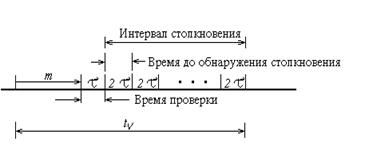
Рис. 5.29. Расчет виртуального времени передачи МДПН/ОС

Общее время до обнаружения столкновения составит 2t единиц времени , что и показано на рисунке.

Если произошло столкновение, предположим, что для его разрешения потребуется 2tJ единиц времени. J представляет собой среднее число повторных передач после того, как произошло столкновение. Оно сравнимо с параметром

E=G/S-1, который был введен при изучении системы Алоха. Тогда виртуальное время передачи имеет вид:

t_v = m + t + 2tJ = m [1+a(1+2J)], aºt/m (5.13)

Далее найдем величину J. Она зависит от стратегии повторной передачи.

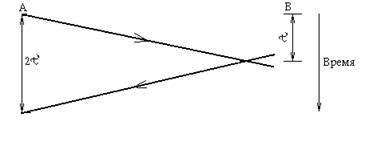
Рис. 5.30 Наихудший случай обнаружения столкновения

Предположим, что длительность интервала столкновения (рис. 5.29) описывается геометрическим распределением единиц 2t с параметром u. В частности, интервал равен одной единице (2t) с вероятностью u, двум единицам с вероятностью u*(1-u) и т.д. Таким образом, u является вероятностью успеха в конце интервала, а (1-u) - вероятностью столкновения. Среднее число повторных передач J=1/u, а именно

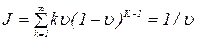
Это рассуждение переносит тяжесть нахождения J на u.

Теперь вероятность u находится путем следующего рассуждения.

Пусть в возможных передачах участвуют n станций (n >> 1). Пусть вероятность того, что одна станция намеревается передавать в промежутке времени 2t c, равна p. Тогда вероятность того, что передает одна станция, и эта передача успешн

u = n p (1-p)^n-1 (5.14)

Используя величину p=1/n и учитывая, как предполагалось, что n >> 1, в пределе получим, что

u_max = (1-1/n)^n-1 ® e ^-1, n ®¥

Таким образом, величина u, которую нужно подставить в (5.14), равна e ^-1. И равенство (5.13) принимает вид:

t_v = m [1+a(1+2e)], a º t / m (5.15)

Заметим, что эта модель повторной передачи напоминает синхронную Алоху и фактически приводит к величине производительности синхронной Алохи e^-1.

Максимальная производительность l_max в числе сообщений за единицу времени равна 1/t_u. Обозначая через l среднее число сообщений, передаваемых по каналу за единицу времени от всех пользователей, и нормируя его относительно пропускной способности 1/m (в сообщениях за единицу времени), из (5.15) находим

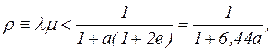а º t / m

Пусть в качестве примера а=0.1. Это значит, что длительность сообщений в 10 раз больше времени распространения сигнала из конца в конец. Для этого значения а имеем

r < 0.6

Очевидно, что это существенное улучшение по сравнению с эффективностью 0.18 для чистой Алохи и 0.368 для синхронной Алохи. Если значение а уменьшить еще больше (путем сокращения длины кабеля или уменьшения пропускной способности в бит/с с целью увеличения m), соответственно увеличится r_max, приближаясь к максимально возможному
значению 1.

Манчестерский код

Кроме проверки двух сигналов - обнаружения столкновения и проверки несущей, - блоки доступа к каналу передают символы в коаксиальный кабель и принимают их из кабеля. Блок кодирования передаваемых данных физического уровня кодирует символы в двоичные сигналы с помощью манчестерского кода. Пример такого кода показан на рисунке 5.31.

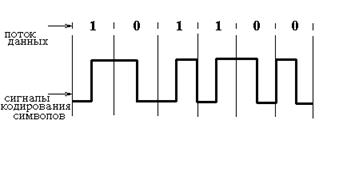
Рис. 5.31. Манчестерский код

При этой схеме половина символьного интервала применяется для передачи логического дополнения к разряду этого интервала; в течение второй половины передается исходное значение этого разряда. Таким образом, единицы передаются положительным переходом сигнала, а нули - отрицательным переходом (рис. 5.31). Функции кодирования/декодирования манчестерского кода выполняются передающим блоком кодирования и приемным блоком декодирования физического уровня. Эти блоки также генерируют и удаляют 64-разрядные серии, называемые преамбулами, которые предшествуют фактически передаваемому кадру и применяются для синхронизации.

Процедура кодирования , определенная стандартом для кольца с передачей метки, предусматривает применение дифференциального манчестерского кода. Этот метод отличается от применения описанного выше манчестерского кода.

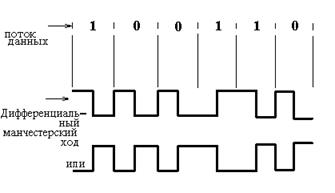
Рис. 5.32. Дифференциальный манчестерский код

В дифференциальном манчестерском коде для переноса двоичной информации применяются две полярности, и переходы происходят в середине двоичного интервала. Однако, в случае разряда 1 первая половина двоичного интервала несет ту же полярность, что и вторая половина предыдущего интервала. В случае же разряда 0 переход происходит как в начале, так и в середине двоичного интервала. Пример на рисунке 5.32 показывает, что при этой процедуре возникают две возможности в зависимости от полярности в конце интервала, предшествующего первому интервалу на рисунке.