Парный линейный корреляционно-регрессионный анализ
Основные положения парного линейного корреляционно-регрессионного анализа представлены на рисунке 16.

Рис. 16. Основные положения парного линейного КРА
Рассмотрим применение парного линейного корреляционно-регрессионного анализа. При линейном выражении зависимости между признаками 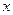 и
и 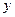 используется уравнение прямой:
используется уравнение прямой:
 (уравнение регрессии),
(уравнение регрессии),
где 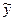 – теоретические значения результативного признака;
– теоретические значения результативного признака;
х – индивидуальные значения факторного признака;
а0, а1 – параметры уравнения регрессии.
Для определения параметров уравнения прямой а0 и а1 на основе требований метода наименьших квадратов составляется система нормальных уравнений:
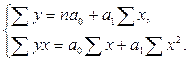
Для решения системы применяется способ определений, позволяющий сводить к минимуму неточности округлений в расчетах параметров уравнений регрессии:

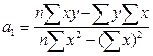 ,
,
где у – фактические (эмпирические) значения результативного признака;
n – количество единиц совокупности (то есть заданных пар значений х и у).
Подставляя в уравнение прямой найденные параметры а0, а1 и значения х, рассчитываем выровненные (теоретические значения) результативного показателя 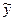 . В уравнении прямой параметр а0 экономического смысла не имеет. Параметр а1 является коэффициентом регрессии и показывает, насколько изменяется в среднем значение результативного признака при увеличении факторного признака на единицу.
. В уравнении прямой параметр а0 экономического смысла не имеет. Параметр а1 является коэффициентом регрессии и показывает, насколько изменяется в среднем значение результативного признака при увеличении факторного признака на единицу.
Часто исследуемые признаки имеют разные единицы измерения, поэтому для оценки влияния факторного признака на результативный рассчитывается коэффициент эластичности в среднем для всей совокупности:
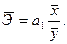
Коэффициент эластичности показывает, на сколько процентов в среднем изменится результативный признак при увеличении факторного признака на 1%.
Для измерения тесноты связи между признаками применяются линейные коэффициенты корреляции и детерминации.
Линейный коэффициент корреляциивычисляется по формуле:
 ,
,
где значение r лежит в пределах от –1 до +1. При  не существует линейной корреляционной связи. Степень тесноты линейной зависимости растет при приближении к
не существует линейной корреляционной связи. Степень тесноты линейной зависимости растет при приближении к 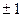 (табл. 16).
(табл. 16).
Таблица 16
Оценка тесноты и направления связи
| Теснота связи | Величина коэффициента корреляции | |
| прямая связь | обратная связь | |
| слабая | 0,1-0,3 | (-0,1)-(-0,3) |
| средняя | 0,3-0,7 | (-0,3)-(-0,7) |
| тесная | 0,7-0,99 | (-0,7)-(-0,99) |
Линейный коэффициент детерминации (r2) – квадрат коэффициента корреляции, выраженный в процентах. Показывает, какая доля вариации результативного признака объясняется вариацией факторного.
Для проверки значимости уравнения регрессии рассчитывают F-критерий Фишера:
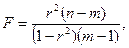
где n – число наблюдений;
m – число параметров.
Рассчитанное значение F-критериясравнивается с критическим (табличным) Ft с уровнем значимости 0,01 или 0,05 и числом степеней свободы (m-1), (n-m). Если рассчитанное значение F оказывается больше табличного, то уравнение регрессии признается значимым. В противном случае следует пересмотреть форму уравнения или перечень переменных.
Значимость коэффициента корреляции осуществляют с помощью t-критерия Стьюдента, который рассчитывается по следующей формуле:
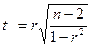 .
.
Рассчитанное значение t-критерия сравнивается с критическим (табличным) значением t-распределения Стьюдента с уровнем значимости 0,01 или 0,05 и числом степеней свободы (n-2). Если рассчитанное значение t оказывается больше табличного, то линейный коэффициент корреляции признается значимым. В противном случае следует увеличить количество наблюдений.
Дата добавления: 2015-11-06; просмотров: 1744;
