Структура ряда динамики. Выявление основной тенденции развития

Ряд динамики состоит из нескольких составляющих:

1) тренд (основная тенденция развития) – достаточно плавное и устойчивое изменение уровня явления во времени, более или менее свободное от случайных колебаний;

2) сезонная составляющая, характеризующая колебания ряда в зависимости от сезона;

3) циклическая составляющая, характеризующая колебания уровней ряда с периодом колебаний в несколько лет;

4) случайные колебания. В отличие от тренда, сезонной и циклической компонент, которые являются регулярными, или систематическими компонентами, случайная является нерегулярной и остается от динамического ряда после выделения из него регулярных компонент.

Выделение тренда может осуществляться методами укрупнения интервалов, скользящей средней и аналитического выравнивания.

Суть метода укрупнения интервалов состоит в преобразовании фактического ряда динамики в ряды более продолжительных периодов (месячные в квартальные, квартальные в годовые и т.д.). Средняя, исчисленная по укрупненным интервалам, позволяет выявить направление основной тенденции развития.

Суть метода скользящей средней состоит в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из того же числа уровней, начиная со второго, далее – начиная с третьего и т.д. Таким образом, при расчетах среднего уровня как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий. Период скользящей может быть четным и нечетным. Удобнее использовать нечетный период, так как в этом случае скользящая средняя будет отнесена к середине периода скольжения. Скользящие средние с продолжительностью периода, равной 3, следующее:

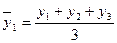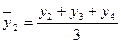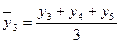; ; и т.д.

Полученные средние записываются к соответствующему срединному интервалу (второму, третьему, четвертому и т.д.).

Если период скользящей четный, то выполняют центрирование данных, т.е. определение средней из найденных средних, что необходимо для определения срединного периода. Например, если исчисляется скользящая с продолжительностью периода, равной 2, то расчет производится следующим образом:

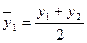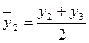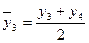; ; и т.д.

Тогда центрированные средние равны:

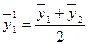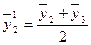; и т.д.

Первая центрированная средняя будет отнесена ко второму периоду, вторая – к третьему и т.д.

Сглаженный ряд «укорачивается» по сравнению с фактическим на 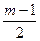члена с одного и другого конца, где 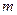– количество уровней, входящих в интервал.

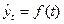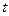Суть метода аналитического выравнивания состоит в нахождении уравнения, выражающего закономерность изменения явления как функцию времени , где – время. При этом на практике чаще всего применяются следующие виды трендовых моделей (табл. 19).

Таблица 19

Виды трендовых моделей

Наименование функции	Вид функции	Применяется
Линейная		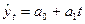Если более или менее постоянны цепные абсолютные приросты
Параболическая		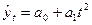Если изменение уровней ряда происходит с приблизительно равномерным ускорением или замедлением цепных абсолютных приростов
Степенная		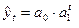Если уровни ряда динамики выявляют тенденцию постоянства цепных темпов роста

Рассмотрим технику выравнивания ряда динамики по линейной функции. Выровненные уровни ряда динамики в этом случае вычисляются по уравнению:

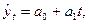
где 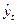– выравненный (теоретический) уровень ряда динамики;

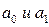– параметры линейной функции;

t – условное обозначение времени.

Параметры 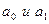находятся по методу наименьших квадратов с помощью решения системы нормальных уравнений:

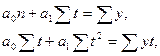
где у – фактический (эмпирические) уровень ряда динамики;

n – число уровней ряда.

Для упрощения исчисления 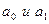допускается условное обозначение времени 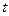таким образом, чтобы Σt = 0. При нечетном числе уровней ряда условное обозначение времени 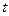будет иметь вид: (…, -3, -2, -1, 0, +1, +2, +3, …). При четном числе уровней ряда условное обозначение времени 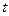будет иметь вид: (…, -3, -2, -1, +1, +2, +3, …). В обоих случаях Σt = 0, тогда:

Параметр 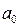характеризует выровненный, свободный от случайных колебаний исходный уровень ряда при 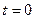, 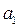– средний абсолютный прирост, показывающий направление основной тенденции развития.

Для оценки степени приближения выравненных уровней к фактическим уровням следует сравнить сумму уровней ряда ( 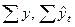), рассчитать остаточное среднее квадратическое отклонение и коэффициент вариации по следующим формулам:

,

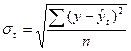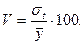
Если коэффициент вариации меньше 25%, а суммы ( 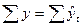) примерно равны, это свидетельствует о достаточном приближении теоретических уровней ряда к фактическим.

Исследование динамики явлений и установление основной тенденции развития дают основание для прогнозирования (экстраполяции) –определения будущих размеров уровня экономического явления. Используют следующие методы экстраполяции:

1) средний абсолютный прирост;

2) средний темп роста;

3) экстраполяцию на основе выравнивания по какой-либо аналитической формуле.