Лекция 10. Явление электромагнитной индукции
§ 10 – 1 Электромагнитная индукция.
Из школьного курса физики известно, что при изменении магнитного поля, пронизы-вающего некую поверхность, ограниченную замкнутым проводящим контуром, в этом контуре возникает ЭДС, равная с обратным знаком скорости изменения магнитного потока. Это явление было откпыто в 1831 году известным английским ученым М. Фарадеем, и установленный им закон носит его имя. Определяя величину магнитного потока Ф как
Ф =BS cosa = 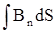 ,
,
где a - угол между направлением В и нормали к площади контура, закон Фарадея можно записать в виде:
E = - 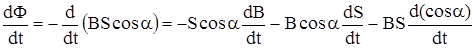 ;
;
откуда видно, что возникновение индукционноготока возможно при изменении либо вели-чины В, либо при изменении площади контура, либо при изменении ориентации контура (вращении) относительно направления магнитного поля. Магнитный поток прято измерять в Веберах. 1 Вебер = 1Тесла ´ м2.
Знак минус, стоящий перед производной магнитного потока отражает правило Лен-ца:индукционный ток направлен так, чтобы своим действием воспрепятствовать причине, его вызвавшей.
Проявлением индукционных токов являются токи Фуко, возникающие в массивных проводниках, помещенных в изменяющееся магнитное поле (например, в сердечниках трансформаторов). Для борьбы с этими токами сердечники набираются из очень тонких листов металла, разделенных прослойкой непроводящего лака.
§ 10 – 2 Самоиндукция.
Важным частным случаем электромагнитной индукции является самоиндукция, т.е. возникновение ЭДС индукции в самом проводнике, порождающим изменяющееся магнит-ное поле. В строгой теории электромагнетизма показано, что величина магнитного потока, окружающего проводник с током, пропорциональна силе этого тока Ф = L I, где коэффици-ент пропорциональности L носит название коэффициента самоиндукции или индуктив-ности.
Качественные соображения о пропорциональности между Ф и I вытекают из закона Био-Савара-Лапласа, где установлено, что В~ I. Значения L определяются геометрическими свойствами проводника. Единицей измерения L в системе СИ служит Генри.
1Генри =1Вебер/Ампер.
Учитывая взаимосвязь Ф и L, можно записать
Eсам = - 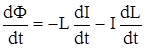 .
.
Если проводник не изменяет своей формы с течением времени, то dL/dt = 0, и
Eсам = - 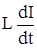 .
.
Для одного витка длинного соленоида Ф =ВS= m0 nIS, и, если полное число витков соле-ноида равно N= nlc, , то общий поток через весь соленоид Ф0 = Ф N = m0 n2lc IS, откуда
L = m0 n2lcS.
§ 10 – 3 Энергия магнитного поля.
Пусть имеется электрическая цепь, состоящая из источника постоянного тока, сопро-тивления и катушки индуктивности L. Предположим, что в некоторый момент времени источник мгновенно удаляется из цепи, которая остается замкнутой. Как следствие явления самоиндукции ток в цепи не исчезнет мгновенно, т.к. его будет поддерживать возникшая ЭДС самоиндукции. В процессе убывания тока сторонние силы, ответственные за явление самоиндукции, совершат некоторую работу. За малый промежуток времени dt, когда ток и ЭДС остаются практически неизменными, сторонние силы совершат работу dA = Eсамdq, где dq =Idt, или, используя выражение для ЭДС самоиндукции, dA= -Idt´L dI/dt, т.е.
dA=-LidI.
Полную работу сил можно найти, суммируя малые работы dA за весь период исчезновения тока:
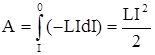 .
.
По закону сохранения энергии эта работа может быть совершена лишь за счет энергии W, которой обладает катушка с током, поэтому
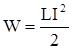 .
.
Эту энергию можно приписать магнитному полю катушки (соленоида). Считая соленоид достаточно длинным, можно использовать формулу, связывающую индукцию поля в соле-ноиде с током: B =m0 nI, откуда I = B/m0 n. Подставляя это соотношение, а также значение L для соленоида в выражение для энергии катушки, получаем:
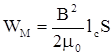 .
.
Тогда плотность магнитной энергии, т.е. энергии, приходящейся на единицу объема V=lcS,
равна
 w =
w = 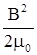 .
.
Дата добавления: 2015-11-06; просмотров: 901;
