Лекция 8. Теорема о циркуляции магнитного поля.

§ 8 –3 Теорема о циркуляции магнитного поля.

Пусть имеется тонкий бесконечный провод, по которому проходит ток силой I. Выберем мысленно окружность радиуса R, концентрическую заданному току и лежащую в плоскос-ти, перпендикулярной ему. Рассмотрим сумму произведений проекций вектора магнитной

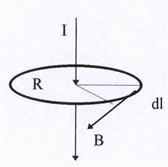Рис.21. Вычисление цир- куляции.

индукции на соответствующий элемент длины окружности ра-диуса R ( рис.21) Bldl. Если суммирование проводится по всей длине окружности, то результат носит название циркуляции, т.е. его можно за-писать так 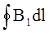.Для выбранного нами контура в виде окруж-ности величина интеграла может быть вычислена непосред-ственно. Во всех точках контура вектора В направлены по касательной к окружности, а значения В постоянны и равны В = 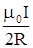, так что его можно вынести за знак интеграла. Тогда

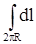= 2pR и циркуляция .

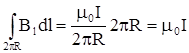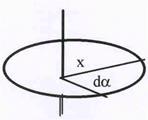Рис.22. К расчету элемента контура.

Если мысленный контур не концентричен току, то результат суммирования не меняется, т.к. для любого элемента контура (см. рис.22) Вl dl = 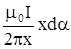и не зависит от расстояния х от тока до элемента контура. Угол da означает малый угол, под которым виден элемент длины контура из точки пересечения его площади током. Очевидно, что полное значение суммирования не изменится и для произвольной формы контура, который удобно в этом случае

представить как ломаную линию, состоящую из элементов окружностей и приращений ра-диуса. Здесь следует помнить, что проекции вектора В на приращения радиуса равны нулю.

Если плоскость, в которой лежит наш мысленный контур, не перпендикулярен на-правлению тока, то контур можно спроектировать на плоскость, нормальную к току, снова результат вычисления циркуляции будет прежний. Если через плоскость нашего контура проходит несколько токов I₁, I₂ и т.д., то поскольку выражение для циркуляции остается справедливым для каждого тока в отдельности, оно останется справедливым и для суммы токов. Итак, в общем можно записать:

.

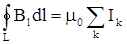Полученное выражение носит название теоремы о циркуляции и является одним из уравнений Максвелла. Суммирование в правой части этого уравнения носит алгебраи-ческий характер: токи могут иметь знак (+) или (-) в зависимости от того, острый или тупой углы образуют они с направлением заданной нормали к площади, охватываемой контуром.

Поля, циркуляция которых отлична от нуля, называются вихревыми.

Словесная формулировка теоремы о циркуляции: