Лекция 18. Поляризация света. Взаимодествие света с веществом.
§18-1 Явление поляризации.
Обычно считается, чтопонятие поляризации связано с сохранением неизменной ориен-тации плоскости колебаний. Говорить о поляризации имеет смысл только для поперечных колебаний. Свет, как мы знаем, является электромагнитной волной, а эти волны – попереч-ны и поляризованы (см.рис.37) так, что казалось бы, световые колебания всегда должны быть поляризованы. Однако мы знаем, что световые волны испускаются отдельными цуга-ми, продолжительность которых не превышает 10–8 сек. Процесс испускания является слу-
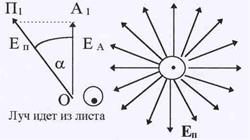 Рис.53. Прохождение света через
анализатор и поляризатор. Рис.53. Прохождение света через
анализатор и поляризатор.
| чайным, и фаза испущенной волны, а также ориента-ции векторов Е и В в плоскости, пер пендикулярной направлению излучения, могут быть любыми.Т.к. вектора Е и В в волне жестко связаны друг с другом, имеет смысл рассматривать лишь один из них (пусть, для определенности, это будет вектор Е). В среднем, в любой волне все допустимые ориентации вектора Е равновероятны (см. рис.53). Существуют приспобле-ния, называемые поляризаторами, которые обладают способностью пропускать через себя световые лучи |
только с одним направлением плоскости колебаний электрического вектора Е, так что на выходе поляризатора свет становится плоско (линейно) поляризованным. Человеческий глаз не в состоянии обнаружить, поляризован свет или неполяризован. Для того, чтобы обнаружить это, необходимо использовать второе такое же приспособление, которое на-зывают анализатором. Если направление пропускания анализатора и поляризатора совпа-дают, луч света на выходе из анализатора имеет максимальную интенсивность. При про-извольном угле a между направлениями анализатора и поляризатора (см.рис.53) амплитуда световых колебаний, выходящих из анализатора ЕА = ЕП cosa, где ЕП – амплитуда колеба-ний на выходе из поляризатора. В электромагнитной волне плотность энергии (интенсив-ность) пропорциональна квадрату амплитуды колебаний Е, т.е. I П ~ Е  и IА ~ Е
и IА ~ Е 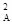 . На осно-вании этого получаем:
. На осно-вании этого получаем:
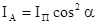 .
.
Это соотношение называется законом Малюса.
§18-2 Закон Брюстера.
Простейшим приспособлением для поляризации света может служить прозрачное диэлектрическое зеркало. Пусть на диэлектрик (см. рис.54) падает луч естественного све-
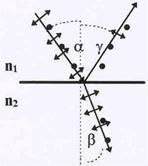 Рис.54. Поляризация света при отражении и преломлении.
Рис.54. Поляризация света при отражении и преломлении.
| та. Обозначим через n2 коэффициент преломления диэлектрика, а через n1 – коэффициент преломления среды, откуда падает свет (a - угол падения, b - угол преломления). Условимся изображать направление колебаний вектора Е в виде точек или тонких чер-точек, где точка изображает направление вектора, перпендику-лярное плоскости чертежа, а черточка означает, что вектор Е ле-жит в плоскости чертежа. В естественном свете равновероятны все направления колебаний Е, что изображается в виде того, что количество точек и черточек одинаково. Опыт показывает, что отраженный и преломленнвй лучи становятся частично поляри-зованными, причем в отраженном свете преобладающими ста-новятся колебания, плоскость которых перпендикулярна плос- |
кости чертежа, а в преломленном предпочтительнее оказываются направления колебаний в плоскости чертежа ( на рис. это изображается в виде преимущества числа точек или черто-чек). Существует угол падения, при котором отраженные лучи становятся полностью поля-ризованными. Этот угол называется углом Брюстера, его значение связано с отношением n2/n1 = n21, т.е. относительным показателем преломления:
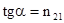 .
.
Качественное объяснение этого закона следует из рассмотрения микроскопической картины распространения светв в веществе. Рассмотрим упрощенную модель взаимодействия света с веществом, согласно которой переменное электрическое поле световой волны приводит в двихение атомы вещества. Атом же представим как диполь, где роль отрицательного заряда
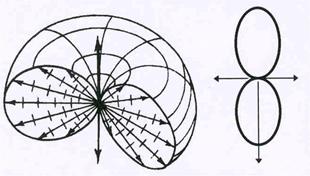 Рис.55. Индикатрисса излучения диполя.
Рис.55. Индикатрисса излучения диполя.
| играет внешний электрон, а вся остальная часть атома рассматривается как положи-тельный заряд (ион). Т.к. масса положитель-ного иона во много раз ( более 2000) больше, чем масса электрона, можно рассматривать лишь колебания электрона. Строгая теория электромагнетиза показывает, что колеблю-щийся диполь становится излучателем элек-тромагнитных волн, причем интенсивность излучения различна в разных направлениях. Для иллюстрации анизотропности излуча- |
тельной способности диполя строится диаграмма (индикатрисса), на которой интенсивность излучения в заданном направлении изображается в виде вектора. Длина этого вектора и ха-рактеризует интенсивность излучения. Пространственное изображение индикатриссы при-ведено на рис.55. В правой части рисунка показано сечение диаграммы вертикальной пло-скостью, проходящей через центр диаграммы.
Положения рассмотренной модели применим для объяснения закона Брюстера. В па-дающем на границу раздела двух сред естественном свете вектор Е принимает всевозмож-ные направления (см.рис.53), но без ограничения общности можно рассматривать лишь два:
       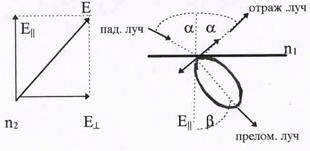
   Рис.56. К выводу закона Брюстера. Рис.56. К выводу закона Брюстера.
| Е и Е , т.к. любой вектор Е можно пред-ставить как их сумму (см. левую часть рис.56). Вектор Е соответствует колебани-ям, которые происходят в направлении, пер-пендикулярным плоскости чертежа,а Е ха-рактеризует колебания в этой плоскости. Представляет интерес рассмотреть лишь со-ставляющую Е .Если диполь излучает волну Е в направлении преломленного луча ( пра- |


 вая часть рис.56), то из диаграммы направленности следует, что в направлении,перпендику-лярном этому лучу, никакого излучения не происходит. В этом направлении излучаются лишь волны с напряженностью Е . Из этого следует, что если луч преломленный и луч от-раженный перпендикулярны друг другу, то в отраженном свете полностью отсутствуют ко-лебания с Е .Из рисунка видно, что b +a + 900 = 1800,или b+a =900, тогда как из закона преломления следует, что sina = n21 sinb . Подставляя в закон преломления b = 900 - a , по-лучим sina = n21sin(900 -a) = n21cosa, т.е.
вая часть рис.56), то из диаграммы направленности следует, что в направлении,перпендику-лярном этому лучу, никакого излучения не происходит. В этом направлении излучаются лишь волны с напряженностью Е . Из этого следует, что если луч преломленный и луч от-раженный перпендикулярны друг другу, то в отраженном свете полностью отсутствуют ко-лебания с Е .Из рисунка видно, что b +a + 900 = 1800,или b+a =900, тогда как из закона преломления следует, что sina = n21 sinb . Подставляя в закон преломления b = 900 - a , по-лучим sina = n21sin(900 -a) = n21cosa, т.е.
tga = n21.
§18-3 Поглощение света.
При прохождении света через вещество часть энергии световой волны поглощается, переходя во внутреннюю энергию вещества. Для оценки величины этих по-терь рассмотрим световой поток, распространяющейся вдоль оси х (рис.57).0пыт показы-вает,что при прохождении очень тонкого слоя вещества толщиной dx относительная убыль
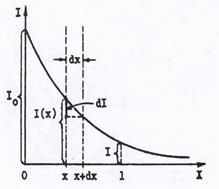 Рис.57. Изменение интенсивнос-
ти света при его поглощении.
Рис.57. Изменение интенсивнос-
ти света при его поглощении.
| интенсивности, т.е.отношение изменения интенсив-ности dIв этом слое к интенсивности падающего света I(х) ( см.рис.57),пропорциональна толщине слоя:
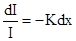 ,
где коэффициент К, зависящий от свойств вещества, называется коэффициентом поглощения.Знак минус отражает убывание интенсивности с ростом х. Измене-ние интенсивности света при прохождении слоя конеч-ной толщины х находится путем прямого интегри-рования вышеприведенной формулы: ,
где коэффициент К, зависящий от свойств вещества, называется коэффициентом поглощения.Знак минус отражает убывание интенсивности с ростом х. Измене-ние интенсивности света при прохождении слоя конеч-ной толщины х находится путем прямого интегри-рования вышеприведенной формулы:
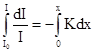 . .
|
Потенцируя последнюю формулу, получим известный закон Бугера: 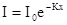 .
.
§ 18 - 4 Рассеяние света.
Плоская волна, распространяющаяся в однородной среде, остается плоской.Однако если среда неоднородна и в ней имеются включения с другими оптическими свойствами, то кроме волны, распространяющейся в первоначальном направлении, появляются волны, рассеянные в стороны. Эти волны уносят часть энергии и уменьшают интенсивность первоначального луча. Характер рассеяния зависит от размеров и природы неоднородностей.Если их размеры больше длины волны.то наблюдается чисто геометрическое рассеяние.Это касается прежде всего твердых частиц, взвешенных в воздухе.Падающий на разные участки поверхности частицы солнечный свет отражается под различными углами. Если при этом спектральный состав света не меняется, то рассеянный свет остается белым (примером это-го может служить белый цвет неба в пустынях.когда восходящие воздушные потоки пере-носят в верхние слои атмосферы мелкие частицы песка). В целом наблюдаемая картина рас-сеяния очень чувствительна к размерам и форме неоднородностей( радуга и гало вокруг солнца, вызванные наличием в земной атмосфере соответственно капелек и льдинок).
Если размеры неоднородносей существенно меньше длин волн света, то интен-сивность рассеянного света удовлетворяет закону Рэлея: Iрас~ Io w4 , где w -частота падаю-щего света, причем интенсивность рассеянного света различна по разным направлениям (т.е анизотропна). Сильная зависимость интенсивности рассеянного света от частоты означает,
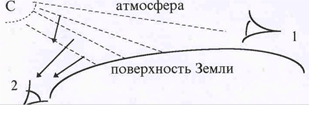 Рис.58. Рассеяние света в атмосфере.
Рис.58. Рассеяние света в атмосфере.
| что существенно сильнее рассеиваются вол-ны с большей частотой. В частности, если через среду идет волна от источника белого света (от Солнца - см.рис.58),то при наблю-дении сбоку среда кажется голубоватой, а сам источник на просвет выглядит более красным. Этим объясняется голубой цвет неба и красный цвет зари. Разные цветовые оттенки получаются из-за разных геометри- |
ческих расположении источника и наблюдателя. Так в глаз наблюдателя 1 ( см.рис.) прихо-дит прямой луч, тогда как наблюдатель 2 видит, в основном, рассеянные лучи.
§ 18 - 5 Дисперсия света.
Дисперсией называется зависимость скорости распространения световой волны в среде от частоты. Поскольку скорость волны однозначно связана с показателем прелом-ления среды ( v = c/n; n = 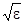 ), то нашей задачей будет выяснение характера зависимости диэлектрической постоянной от частоты. Здесь уместно напомнить, что e =1+ k (k - диэлектрическая восприимчивость, определяющая соотношение между поляризацией ве-щества Р и действующем электрическим полем Е : Р = eо kЕ ).В то же время величина вектора поляризации определялась как суммарный дипольный момент единичного объема: Р =Nqx, гдe величина qx характеризует дипольный момент каждой молекулы диэлектрика. При решении задачи будем пользоваться той же моделью.что применялась ранее при рас-
), то нашей задачей будет выяснение характера зависимости диэлектрической постоянной от частоты. Здесь уместно напомнить, что e =1+ k (k - диэлектрическая восприимчивость, определяющая соотношение между поляризацией ве-щества Р и действующем электрическим полем Е : Р = eо kЕ ).В то же время величина вектора поляризации определялась как суммарный дипольный момент единичного объема: Р =Nqx, гдe величина qx характеризует дипольный момент каждой молекулы диэлектрика. При решении задачи будем пользоваться той же моделью.что применялась ранее при рас-
 |
смотрении закона Брюстера. Под действием переменного электрического поля световой волны расстояние электрона до положительного иона периодически изменяется.т.е. элек-трон совершает вынужденные колебания под действием внешней периодической силы.Вид этого уравнения, и его решение уже изучались ( см уравнение колебаний в кон-туре).Поэтому можно сразу написать выражение для амплитуды колебаний электрона в атоме:
где b характеризует затухание колебаний, а w0 может рассматриваться как собственная частота колебаний электрона в атоме.Для упрощения математических выкладок будем пренебрегать затуханием,т.е положим b = 0.Тогда величина поляризации равна:
Р = 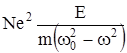 .
.
С другой стороны,выше указывалось,что Р = e0 kЕ, поэтому
k = 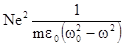 .
.
Тогда e = 1 +k = 1 + 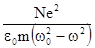 ; e = n2 .
; e = n2 .
Таким образом, имеем:
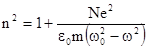 .
.
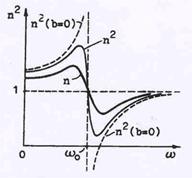 Рис.59 Частотная зависи-
мость показателя прелом-
ления.
Рис.59 Частотная зависи-
мость показателя прелом-
ления.
| График частотной зависимости в сделанных упрощениях по-казан на рис.59. Из рис. видно,что вдали от резонансной частоты показатель преломления (точнее n2 ) возрастает про-порционально квадрату частоты.Такая частотная зависимость получила название нормальной дисперсии. Когда же частота внешних колебаний приближается к частоте собственных, амплитуда возрастает неограниченно.Ясно,однако,что этот результат есть следствие наших упрощений. При наличии за-тухания кривая имеет конечный максимум ( см. рис.59 ). Вблизи резонансной кривой показатель преломления имеет другой характер зависимости. Говорят, что - это область ано-мальной дисперсии, т.к. для нее величина n2 падает с ростом частоты, причем это наблюдается на фоне повышения пог-лощения света (амплитуда колебаний электрона возрастает). |
СОДЕРЖАНИЕ
| № лекции | Содержание лекции | Страница |
| 1. | ЭЛЕКТРОСТАТИКА. Электрический заряд.Электрическое поле. Напряженность электрического поля. | |
| 2. | Теорема Остроградского-Гаусса | |
| 3. | Работа по перемещению заряда в электрическом поле. Потенциал электростатического поля. | |
| 4. | Проводники в ээлектрическом поле | |
| 5. | Диэлектрики в электрическом поле | |
| 6. | Постоянный электрический ток | |
| 7. | МАГНИТНОЕ ПОЛЕ. Постоянное магнитное поле | |
| 8. | Теорема о циркуляции магнитного поля | |
| 9. | Силы, действующие в магнитном поле | |
| 10. | Явление электромагнитной индукции | |
| 11. | Магнитное поле в веществе | |
| 12. | Переменный электрический ток | |
| 13. | Электромагнитные колебания | |
| 14. | Уравнения Максвелла. Электромагнитные волны. | |
| 15. | Представления о свете. Законы геометрической оптики | |
| 16. | Волновая оптика. Явление интерференции | |
| 17. | Дифракция света | |
| 18. | Поляризация света. Взаимодействие света с веществом. Дисперсия света |
Дата добавления: 2015-11-06; просмотров: 949;
