Теорема Кронекера-Капелли.
СИМПЛЕКСНЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
ЗЛП в канонической форме
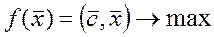 (1)
(1)
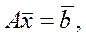 (2)
(2)
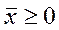 (3)
(3)
Теорема Кронекера-Капелли.
Система (2) имеет решение тогда и только тогда, когда ранг расширенной матрицы равен рангу матрицы системы:
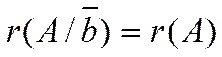 , (4)
, (4)
причём, если r=n, то система (2) имеет единственное решение,
если r<n, то система (2) имеет бесконечное множество решений.
Методом Гаусса среди n переменных можно выделить r базисных переменных и (n-r) свободных переменных, причём базисные переменные могут быть линейно выражены через свободные.
Предположим, что ранг матрицы равен числу уравнений (все условия линейно независимые):
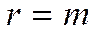 .
.
Определение: Базисным (опорным) решением системы m линейных уравнений с n неизвестными называется решение, в котором все (n-m) свободные переменные равны нулю.
Оставшиеся m базисных переменных образуют базис.
Замечание. Выбор базисных и свободных переменных неоднозначен.
Всего существует 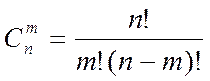 базисных решений.
базисных решений.
Учтем условие неотрицательности переменных.
Определение: Допустимым базисным решением (ДБР) системы (2) называется решение, удовлетворяющее условию неотрицательности (3).
Утверждение.
Допустимое решение ЗЛП является угловой точкой ОДР тогда и только тогда, когда это решение является допустимым базисным.
Дата добавления: 2015-11-06; просмотров: 597;
