Алгоритм симплекс-метода

Шаги алгоритма симплекс метода выполним на конкретном примере.

Рассмотрим ЗЛП:

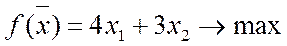(5)

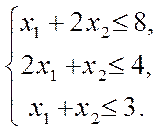(6)

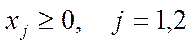
Приведем условия связи к канонической форме:

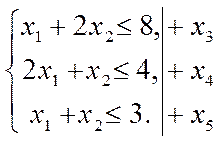
Тогда система ограничений примет вид:

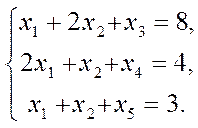(7)

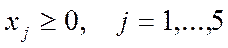
Шаг 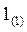. Выбрать базисные переменные (БП) и свободные переменные (СП).

Правило. Если какие-нибудь переменные входят в систему ограничений только в одно уравнение, имея тот же знак, что и свободный член правой части, то эти переменные выбираем в качестве базисных переменных.

Правые части при этом должны быть неотрицательны.

В рассматриваемом примере

БП: x₃, x_4, x₅;

СП: x₁, x₂.

Замечание. Приведение системы к требуемому виду осуществляется на предварительном шаге (шаг 0). Это можно сделать методом Гаусса или методом искусственного базиса.

Шаг 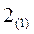. Выразить БП через СП.

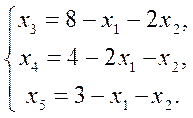(8)

Шаг 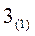. Приравняв СП нулю, найти допустимое базисное решение (опорный план):

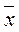¹= (0; 0; 8; 4; 3)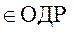

так как все значения неотрицательны.

Шаг 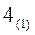. Выразить целевую функцию через СП и вычислить значение целевой функции для найденного 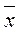¹.

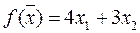
f( 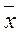¹) = 0.

Шаг . Проверить оптимальность найденного решения.

Если при 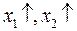целевая функция