Критерий оптимальности решения поиска максимума целевой функции.

Если в выражении линейной целевой функции через СП отсутствуют положительные коэффициенты при СП для задачи поиска максимума, то решение является оптимальным.

Если решение является оптимальным, то наша целевая функция достигла своего максимума и на этом решение задачи закончено, а если нет, то переходим к шагу .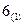

В примере 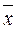¹ – неоптимальное, т.к. все коэффициенты положителены.

Шаг 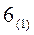. Определить свободную переменную, преходящую в базис и базисную, становящуюся свободной.

Правило: В базис переходит одна из свободных переменных, имеющая положительный коэффициент в целевой функции.

x₁ → БП

Условие неотрицательности переменных в системе (8)

при равной нулю свободной переменной x₂=0:

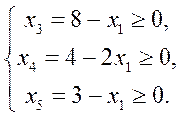
Выпишем значения, до которых может возрастать x_1:

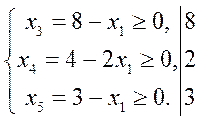
и выберем наименьшее:

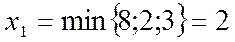
Уравнение системы (8), в котором базисная переменная обращается в нуль, называется разрешающим:

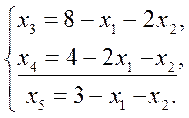
Соответствующая базисная переменная становится свободной.

x₄ → СП.

Повторяем шаги алгоритма.

Шаг .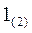

БП: x₁, x_3, x₅;

СП: x₂, x₄.

Шаг

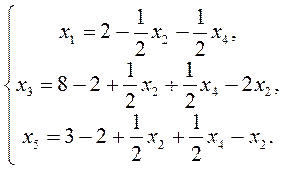
Упрощаем:

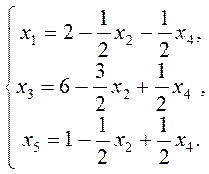
Шаг

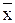² = (2; 0; 6; 0; 1)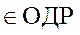

Шаг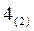

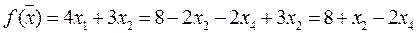
f( 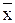²) = 8.

Шаг

Так как коэффициент при x₂ остался положительным, то решение не оптимально.

Шаг

x₂ → БП

При x₄=0

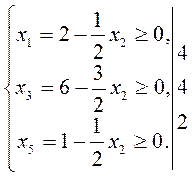
x₂ может возрастать до

.

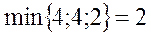Разрешающее уравнение:

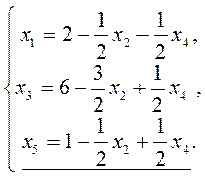
x₅ → СП.

Шаг .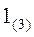

БП: x₁, x_2, x₃;

СП: x₄, x₅.

Шаг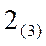

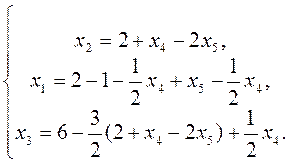
Упрощаем:

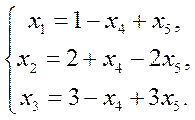
Шаг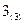

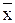³ = (1; 2; 3; 0; 0)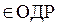

Шаг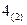

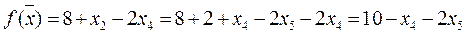
f( 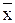³) = 10.

Шаг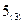

Так как в выражении линейной целевой функции через СП отсутствуют положительные коэффициенты, найденное решение является оптимальным.

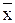_опт = (1; 2; 3; 0; 0)

f_опт= 10.

Замечание:

Случай минимизации целевой функции:

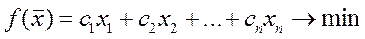
Способ 1.

Рассматривать

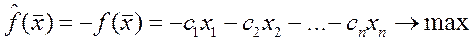
Задача сводится к рассмотренной.

Способ 2.

Изменить критерий оптимальности.