Метод максимального правдоподобия

Наиболее распространенным методом точечных оценок параметров является метод максимального правдоподобия. Этот метод впервые был предложен Р. Фишером.

Пусть по-прежнему имеется выборка 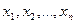из генеральной совокупности с неизвестной теоретической функцией распределения 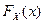, принадлежащей известному однопараметрическому семейству 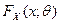. Функция неизвестного параметра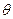

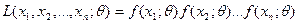
называется функцией правдоподобия. Здесь 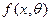- плотность распределения случайной величины Х при непрерывном распределении, а в случае дискретного распределения 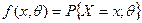. Замечательное свойство функций правдоподобия заключается в том что они как бы вбирают в себя всю информацию, которая дается выборкой относительно параметра 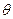. Функция правдоподобия по сути не что иное, как вероятность (в непрерывном случае плотность распределения) получить именно ту выборку 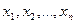, которую бы мы реально имели, если бы значение неизвестного параметра равнялось 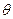. Естественно, поэтому в качестве оценки неизвестного параметра 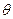выбрать 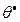, доставляющее наибольшее значение функции правдоподобия 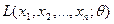. Оценкой максимального правдоподобия называется такое значение 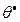, для которого

.

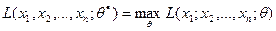На практике используется не саму функцию правдоподобия, а ее логарифм .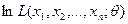

Используя необходимое и достаточное условие экстремума функции, оценка максимального правдоподобия 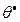может быть найдена следующими действиям:

1. Найти производную 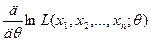, приравнять ее к нулю и найти корень 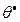уравнения правдоподобия

.

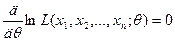2. Найти вторую производную 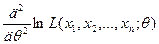и, если при 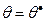вторая производная отрицательна, то 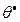- оценка максимального правдоподобия неизвестного параметра .

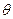Замечание 1. Для использования метода максимального правдоподобия необходимо, что бы функция правдоподобия была дифференцируемой. Оценку 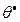следует искать среди значений 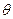, удовлетворяющих уравнению правдоподобия или принадлежащих границе области допустимых значений 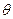. Доя наиболее важных, с практической точки зрения, семейств 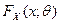уравнение правдоподобия имеет единственное решение 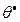. Это решение и является оценкой максимального правдоподобия.

Замечание 2. Метод максимального правдоподобия до настоящего момента был изложен для случая оценки одного параметра 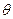. Естественно, что все вышесказанное распространяется и на случай оценки k неизвестных параметров .

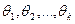Перечислим достоинства метода максимального правдоподобия:

· для случая оценки одного параметра оценки максимального правдоподобия 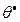всегда будет состоятельной;

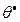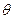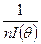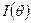· при больших объемах выборки n распределение оценки максимального правдоподобия можно приближенно считать нормальным со средним и дисперсией , где - информация Фишера. Оценка 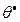будет асимптотически эффективной в том смысле, что не существует другой асимптотически нормальной оценки, имеющей меньшую дисперсию;

· если существует эффективная оценка неизвестного параметра 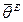, то она является оценкой максимального правдоподобия .

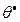Пример 1. Найти методом максимального правдоподобия оценку параметра 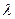распределения Пуассона

,

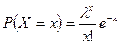пользуясь выборкой, которая дала значения 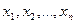для величины Х

Решение. Функция правдоподобия в этом случае имеет вид

.

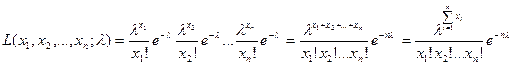Ее логарифм, соответственно, будет таким

.

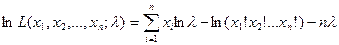Для определения 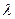выпишем уравнение правдоподобия:

.

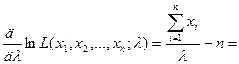
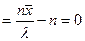Откуда имеем

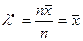
Найдем теперь вторую производную :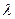

.

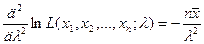Учитывая, что значениями выборки 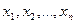могут быть только целые неотрицательные значения k = 0,1,2,…, убеждаемся в том, что при 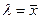вторая производная отрицательна:

.

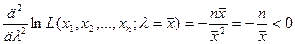Следовательно, оценкой максимального правдоподобия 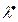параметра 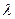для распределения Пуассона будет средняя арифметическая 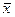. Задача решена.

Хорошей иллюстрацией примера 2 может служить знаменитый опыт Резерфорда, Чедвика и Эллиса, заимствованный из книги [10, гл. 3, § 1]. Радиоактивное вещество наблюдали в течение 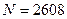промежутков времени, каждый длиной в 7,5 секунд, и для каждого интервала регистрировали число частиц, достигших счетчика. Всего таких частиц было зарегистрировано 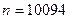. В табл. 3 во втором столбце приведены результаты этих наблюдений, в третьем столбце – отвечающие им частости, а в четвертом – теоретические вероятности, подсчитанные по формуле Пуассона. Причем в качестве параметра 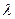была взята, по сути, оценка метода максимального правдоподобия, т.е. среднее число частиц 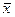за промежуток времени 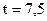секунд:

.

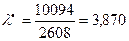Результаты выглядят довольно впечатляюще. Частости, полученные опытным путем, незначительно отличаются от теоретических вероятностей. Этот факт говорит о том, что, во-первых, был верно предугадан тип теоретического распределения (т.е. распределения Пуассона), и, во-вторых, параметр 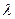теоретического распределения был удачно оценен по значениям статистической выборки.

Табл. 1. Данные опыта Резерфорда, Чедвика и Эллиса

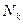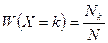
Число частиц k, достигших счетчика	Число наблюдений , в которых регистрировалось k частиц	Частость данного числа частиц	Теоретическая вероятность
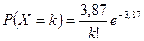
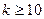
		0,022 0,078 0,147 0,201 0,204 0,156 0,105 0,053 0,017 0,010 0,006	0,021 0,081 0,156 0,201 0,195 0,151 0,097 0,054 0,026 0,011 0,007
Итого		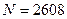0,999	1,000

Замечание 3. В общем случае оценка максимального правдоподобия может быть не только неэффективной, но и смещенной. Однако эта смещенность не имеет существенного значения и может быть исправлена, например, домножением на соответствующий множитель (см. параграф 9.1).

Недостаток метода максимального правдоподобия состоит в том, что он подчас требует сложных вычислений.