Требования к оценкам параметров распределений

В общем случае задача оценки параметров распределения 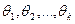сводится к нахождению таких функций 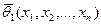, , 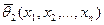…. , 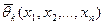которые можно использовать для приближенного определения значений параметров. При этом мы должны быть уверены, что, по крайней мере, при больших объемах выборки 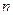можно без существенной ошибки предполагать, что почти наверно

,

,

…………………….

.

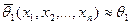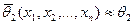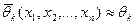Последнее требование сформулируем более точно.

Пусть имеется выборка 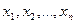наблюдаемых значений случайной величины Х и необходимо оценить параметр 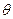, входящий в неизвестную теоретическую функцию распределения 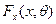. Будем считать значения выборки 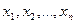случайными величинами 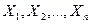с одной и той же функцией распределения 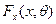. Обозначим через 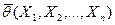оценку параметра .

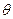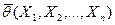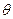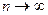Определение 5.1. Оценка называется состоятельной, если она сходится по вероятности к оцениваемому параметру при . Т.е. для любого 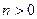выполняется условие

.

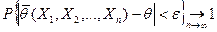Состоятельность - это первое естественное требование, предъявляемое к оценке неизвестного параметра. Состоятельность обеспечивает практическую близость статистической оценки к оцениваемому параметру при больших объемах выборки 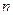. Однако при малых значениях 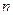их состоятельности оценки нельзя сделать вывод о ее пригодности.

Вторым из естественных требований, часто предъявляемых к оценкам, является требование несмещенности, т.е. отсутствия в ней систематической погрешности.

Определение 5.2. Оценка 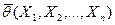называется несмещенной, если при любом конечном 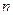(в том числе и при малом) выполняется равенство

.

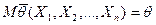Определение 5.3. Оценка называется положительно смещенной, если

,

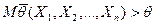и отрицательно смещенной, если

.

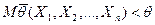Утверждение 5. 1. Если оцениваемый параметр 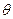является математическим ожиданием случайной величины Х, то несмещенной оценкой для него будет средняя арифметическая .

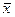Доказательство. Т.к. выборочные значения 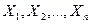одинаково распределены, то .

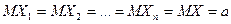Следовательно, имеем

.

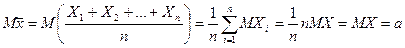Что и требовалось доказать.

Утверждение 5. 2. Если оцениваемый параметр 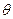является дисперсией 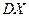случайной величины Х, то примером смещенной оценки может служить эмпирическая (выборочная) дисперсия

.

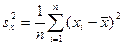В то же время, такая оценка является состоятельной. Несмещенной же оценкой дисперсия

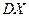является число

.

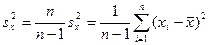Эту характеристику часто называют исправленной дисперсией.

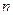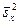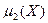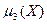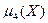Практически эту поправку вносят при вычислении дисперсии, когда объем выборки меньше 30-40. Другими словами, оценка является несмещенной оценкой теоретического второго центрального момента . Для третьего и четвертого теоретических центральных моментов и несмещенными оценками будут:

,

,

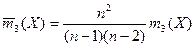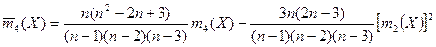где 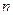- объем выборки, 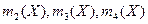- второй и, третий и четвертый эмпирические центральные моменты, соответственно.

Замечание 5. 1. Функция Microsoft Excel ДИСП( ) и СТАНДОТКЛОН( ) рассчитывает несмещенные оценки теоретической дисперсии и теоретического среднего квадратического отклонения, соответственно (следовательно, функции ДИСПР( ), СТАНДОТКЛОНП( ), вычисляют смещенные оценки).

Пример 5. 1. Зная, что выборочная дисперсия 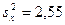, объем выборки 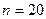, рассчитать исправленную дисперсию .

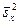Решение. Выборочная дисперсия 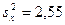является смещенной оценкой генеральной дисперсии 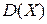. Объем нашей выборки 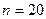. Поэтому исправленная дисперсия (несмещенная оценка) равна:

.

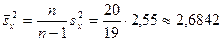Пусть имеются две состоятельные несмещенные оценк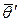и и 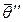для одного и того же параметра 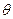. Какой из них следует отдать предпочтение? Лучшей из них является та, у которой меньше дисперсия. Дисперсия статистической оценки рассчитывается стандартным образом:

,

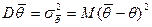где

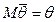
в силу несмещенной оценки.

Т.о., возникает вопрос о нахождении несмещенной состоятельной оценки с наименьшей дисперсией. При весьма широких предположениях дисперсия оценок, построенных по выборке объема 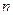, не меньше некоторой нижней границы. Этими вопросами занимались шведский математик Крамер Карл Харальд [18, с. 270], Рао (к сожалению, мы не располагаем биографическими сведениями об этом ученом), английский биолог, математик и статистик Фишер Рональд Аймлер (1890-1962) [там же, с.496].

Утверждение 5. 3 (неравенство Крамера-Рао. Пусть 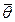несмещенная оценка неизвестного параметра 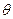, построенная по выборке объема 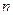. Тогда для дисперсии 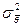этой оценки выполняется неравенство Крамера-Рао:

.

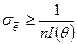Неотрицательную величину 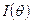называют информацией Фишера. Она определяется из равносильных выражений:

,

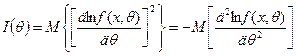где 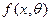- плотность распределения случайной величины при непрерывном распределении. В случае дискретного распределения

.

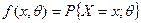Если существует такая несмещенная оценка 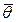, для которой дисперсия 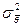достигает нижней границы, равной 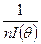, то она называется эффективной оценкой. Эффективную оценку принято обозначать как .

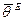Эффективная оценка всегда состоятельна. Если существует какая-либо другая несмещенная оценка 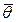, то сравнительную эффективность определяют отношением дисперсией:

.

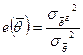Сравнительная эффективность всякой несмещенной оценки не больше единицы.

Пример 5. 2. Для простой случайной выборки из нормальной совокупности эффективной оценкой математического ожидания 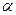является средняя арифметическая 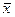, а сравнительная характеристика медианы 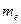при выборке большего объема приближенно равна

.

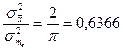Практически это означает, что центр распределения 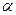определяется по медиане 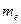с той же плотностью при 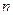наблюдениях, как при 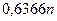наблюдениях по средней арифметической 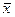. Рис. 1 иллюстрирует соответствующие кривые плотностей.

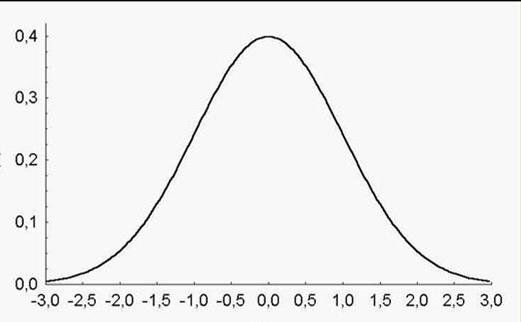
Рис. 1 Кривые плотностей выборочных распределений средней арифметической 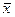(линия) и медианы 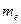(пунктир)
Пример 3. Пусть случайная величина Х представляет частость появлений успеха при возвратной выборке объема 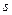. Т.о., случайная величина 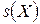- число успехов в 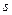испытаниях. Она распределена по биномиальному закону, параметр 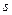которого считается известным. Требуется найти эффективную оценку параметра 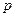этого же закона, т.е. вероятности успеха в единичном испытании, если известны результаты 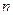выборок объема 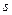. Пусть i-я из произведенных 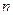выборок объема 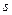дает частость 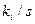, которую можно считать приближенной оценкой для 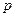. Будем использовать наблюдаемые частости 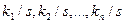для более точной оценки .

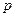Опуская подробности расчетов, имеем

.

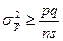Т.е. правая часть неравенства является нижней границей дисперсий для возможных статистических оценок параметра 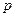при известном 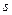. Проверим является ли эффективной следующая статистическая оценка вероятности :

,

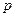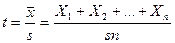где 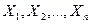- количество успехов в 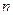возвратных выборках объема 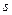. Т.к. 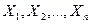- 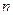одинаково распределенных по биноминальному закону экземпляров величины Х и

,

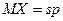то

.

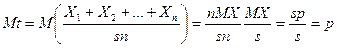Это и доказывает, что статистическая оценка t является несмещенной оценкой для 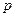. Для биномиальной случайной величины Х дисперсия равна

.

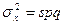Найдем дисперсию оценки t:

.

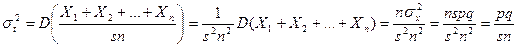Это означает, что статистическая оценка 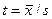является эффективной несмещенной оценкой параметра 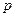при известном объеме .

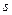Метод моментов.

Пусть имеется выборка 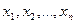из генеральной совокупности с теоретической функцией распределения 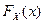, принадлежащей k-параметрическому семейству 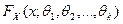с неизвестными параметрами 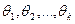, которые нужно оценить. Поскольку нам известен вид теоретической функции распределения, мы можем вычислить первые k теоретических моментов. Эти моменты, разумеется, будут зависеть от k неизвестных параметров :

,

,

…………………….

.

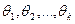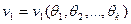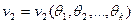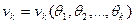Метод моментов заключается в следующем. Т.к. эмпирические моменты являются состоятельными оценками теоретических моментов, то записанной системе равенств при большом объеме выборки 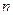теоретические моменты 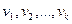можно заменить на эмпирические 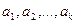. В полученной системе уравнений в роли неизвестных выступают параметры 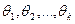. При решении этой системы уравнений будут получены оценки 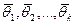неизвестных параметров :

,

…………………….

.

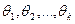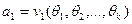
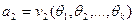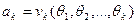Замечание 1. Метод моментов был изложен с использованием начальных моментов. Все вышесказанное имеет место и для центральных моментов.

Метод моментов впервые предложил П.Л. Чебышев [37, с.253]. Развитием метода занимались ученики Чебышева и английский математик, биолог, философ-позитивист Карл Пирсон (1857-1936) [18, с.394]. Кратко суть метода может быть изложена словами: для определения точечных оценок неизвестных параметров заданного распределения необходимо прировнять теоретические моменты рассматриваемого распределения к соответствующим эмпирическим моментам того же порядка.

Пример 1. Страховая компания провела анализ дневных суммарных выплат по однотипным медицинским договорам страхования. Результаты анализа (в тыс. грн.) за 100 рабочих дней сведены в табл.1:

Табл.1. Статистические данные к примеру 1

№ интервала
Границы	0 - 1	1 - 2	2 - 3	3 - 4	4 - 5	5 - 6	6 - 7	7 - 8
Середина интервала	0,5	1,5	2,5	3,5	4,5	5,5	6,5	7,5
Частота
Частость	0,01	0,05	0,14	0,26	0,24	0,18	0,10	0,02	100/100=1

Предполагая, что дневные суммарные выплаты распределены по нормальному закону

.

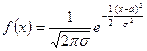оценить методом моментов параметры 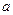и .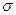

Решение. Вычислим среднее значение выборки, причем за представителя каждого интервала (разряда) примем его середину:

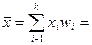
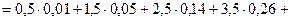
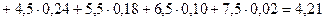
Выборочные дисперсия и стандартное отклонение, соответственно, равны:

,

.

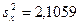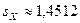Согласно методу моментов, нужно приравнять теоретические моменты рассматриваемого распределения к соответствующим эмпирическим моментам того же порядка. Следовательно, выберем параметры 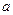и 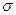нормального закона так, чтобы выполнялись условия:

,

.

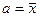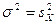Поэтому

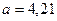
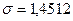
Подставляя оценки параметров, полученные методом моментов, в теоретическую плотность распределения имеем

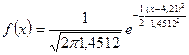
Вычислим значения 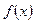в середине каждого из интервалов:

Табл.2.Расчетная таблица к примеру 1

x	0,5	1,5	2,5	3,5	4,5	5,5	6,5	7,5
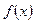
	0,0105	0,0481	0,1373	0,2439	0,2694	0,1852	0,0792	0,0210
Частость	0,01	0,05	0,14	0,26	0,24	0,18	0,10	0,02

Как видно из табл.2 значения плотности распределения в серединах интервалов мало отличается от частости. Построим на рис.1 гистограмму и, по вычисленным значениям, кривую плотности.

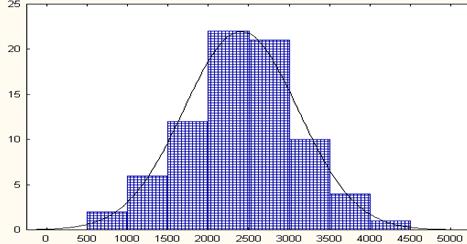
Рис. 1. Гистограмма частостей и кривая теоретической плотности распределения

Судя по рис.1, теоретическая кривая плотности распределения 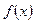, в основном, сохраняет особенности статистического распределения. Пример 1 выполнен.

Замечание 2. Оценки, полученные методом моментов, обычно имеют сравнительную эффективность 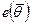существенно меньше единицы и даже являются смещенными. Иногда, из-за простоты их нахождения, они используются в качестве начального приближения для нахождения более эффективных оценок.