Классификация нелинейных функций.

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций. В общем случае линейное уравнение выглядит так, что каждый объясняющий элемент, за исключением постоянной величины, записан в виде произведения переменной и коэффициента

у = a + b₁х₁ + b₂х₂ + ... 4.4.

Уравнения вида

у = a + 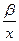4.5.

и у = a х ^b 4.6.

являются нелинейными.

Зависимости (4.5) и (4.6) считаются приемлемыми для описания кривых Энгеля, характеризующих соотношение между спросом на определенный товар (у) и общей суммой дохода (х). Как можно определить параметры a и b в каждом уравнении, зная значения у и х ?

В конечном счете в обоих случаях можно применить линейный регрессионный анализ, для этого потребуется лишь небольшая подготовка. Во-первых, заметим, что уравнение (4.4.) является линейным в двух смыслах. Правая часть линейна по переменным, если определить их в представленном виде, а не как функции. Следовательно, она состоит из взвешенной суммы переменных, а параметры являются весами. Правая часть также линейна по параметрам, так как она состоит из взвешенной суммы параметров. Отсюда различают два класса нелинейных регрессий:

1) регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам. Примером этого класса моделей могут служить полиномы разных степеней у = а + вх + сх²; у = а + вх + сх²+ dх³, а также равносторонняя гипербола

у = в + а/х.

2) нелинейные регрессии по оцениваемым параметрам:

- степенная у = а х^в

- показательная у = а в^х

- экспоненциальная у = е ^{а+ вх}.

Первый класс моделей (нелинейных по переменным) не таит каких-либо сложностей в оценке ее параметров. Она определяется, как и в линейной регрессии, методом наименьших квадратов (МНК), ибо эти функции линейны по параметрам. Так, в параболе у = а + вх + сх² , заменяя переменные х₁=х, а х₂=х² , получаем двухфакторное уравнение линейной регрессии у = а + вх₁ + сх₂. Соответственно для полинома третьего порядка получим трехфакторную модель линейной регрессии и так далее (слайд).Следовательно, полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров. Среди нелинейной полиномиальной регрессии чаще всего используется парабола второй степени, в отдельных случаях – полином третьего порядка. Ограничения в использовании полиномов более высоких степеней связаны с требованием однородности совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и, соответственно, тем менее однородна совокупность по результативному признаку.

Для равносторонней гиперболы мы можем заменить 1/х на z и получим линейное уравнение регрессии, оценка параметров которого может быть дана МНК.

Иначе обстоит дело со вторым классом моделей, то есть с регрессией, нелинейной по оцениваемым параметрам. Данный класс нелинейных моделей можно разделить на два типа: а) нелинейные модели внутренне линейные и б) нелинейные модели внутренне нелинейные.

Если модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Пример – степенная функция у = а х^в. Данная модель нелинейна относительно оцениваемых параметров, так как включает параметры а и в неаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения приводит его к линейному виду(слайд). Соответственно оценки параметров а и в могут быть найдены МНК.

Внутренне нелинейной будет модель вида у = а + вх^с, так как ее невозможно превратить в линейный вид никакими преобразованиями переменных. В нашем начальном курсе эконометрики мы будем рассматривать только модели нелинейные по переменным (то есть первый класс моделей) и модели, нелинейные по параметрам, но внутренне линейные (то есть второй класс, первый тип).