Отдельные виды нелинейных регрессий.

4.3.1.Парабола второй степени целесообразна к применению, если для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную, или обратная на прямую. В этом случае определяется значение фактора, при котором достигается минимальное или максимальное значение результативного признака. Для этого приравнивают к нулю первую производную параболы второй степени

у = а +вх+сх², 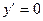, то есть в+2сх=0 и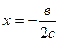

Если же исходные данные не обнаруживают изменения направленности связи, то параметры параболы второго порядка становятся трудно интерпретируемыми, и поэтому форму связи можно заменить другими нелинейными моделями.

Если в>0 и с<0, то кривая симметрична относительно высшей точки, то есть точки перелома кривой, изменяющей рост на падение. В анализе таких функций часто определяется значение фактора, при котором достигается максимум результата. Например, предполагая, что зависимость урожайности от дозы внесения удобрений характеризуется уравнением вида

у = 5 + 1,5х – 0,1х²,

мы найдем величину дозы удобрений, обеспечивающую максимальную урожайность. Приравнивая к нулю первую производную, имеем

1,5 – 2*0,1х = 0

Максимальная урожайность достигается при дозе удобрений

х = 1,5/0,2 = 7,5.

При в<0 и с>0 парабола второго порядка симметрична относительно своей низшей точки. Это позволяет определить минимум функции в точке, меняющей направление связи, то есть снижение на рост (например, найти выпуск продукции, при котором достигаются минимальные удельные затраты).

Чаще всего исследователь имеет дело лишь с отдельными сегментами параболы, а не с полной симметричной параболической формой. Поэтому если график зависимости не демонстрирует четко выраженной смены направленности связи признаков, то она может быть выражена другой нелинейной функцией (например, степенной).