Равносторонняя гипербола.
Среди класса нелинейных функций, параметры которой без особых затруднений оцениваются МНК, следует назвать хорошо известную в эконометрике равностороннюю гиперболу. Для нее, заменив 1/х на z, получим линейное уравнение регрессии
у = а + вz
Гипербола может быть использована не только для характеристики удельных затрат с объемами производства, как уже указывалось ранее. Примером ее использования может служить также взаимосвязь доли расходов на определенные группы товаров (продовольственные, непродовольственные, товары длительного пользования) с общей суммой доходов. Подобного рода взаимосвязи получили название кривых Энгеля. В 1857 году немецкий статистик Энгель сформулировал закономерность – с ростом дохода доля затрат на продовольствие уменьшается. Соответственно, возрастает доля расходов на непродовольственные товары.
Допустим, вы исследуете соотношение между ежегодным потреблением бананов и годовым доходом, и наблюдения приведены в табл.4. 1, где собраны наблюдения для 10 семей (слайд).
Таблица 4.1
| Семья | Бананы (в фунтах) (у) | Доход (в 1000 долл.) (х) | ( z ) |
| 1,93 | 1,000 | ||
| 7,13 | 0,500 | ||
| 8,78 | 0,333 | ||
| 9,69 | 0,250 | ||
| 10,09 | 0,200 | ||
| 10,42 | 0,167 | ||
| 10,62 | 0,143 | ||
| 10,71 | 0,125 | ||
| 10,79 | 0,111 | ||
| 11,13 | 0,100 |
На слайде (рис.4.2). представлено облако точек, соответствующих наблюдениям, а также график уравнения регрессии между у и х 
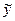 = 5,09 + 0,73 х ; R2= 0,64. (4.7.)
= 5,09 + 0,73 х ; R2= 0,64. (4.7.)
Стандартные ошибки (1,23) (0,20)
Из рисунка видно, что график уравнения регрессии не вполне соответствует точкам наблюдений, несмотря на то, что коэффициент при х существенно отличается от нуля при однопроцентном уровне значимости. Очевидно, что точки наблюдений лежат на кривой, тогда как уравнение регрессии характеризуется прямой. В данном случае нетрудно заметить, что функциональная зависимость между у и х определена неправильно.
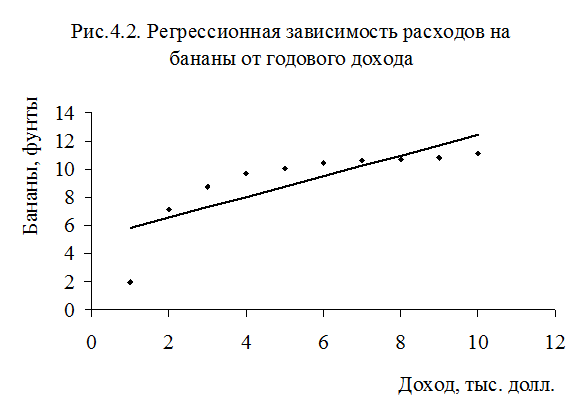
В том случае, если вы не можете представить зависимость в графическом виде ( например, если вы используете множественный регрессионный анализ), понять, что где то допущена ошибка, можно с помощью анализа остатков. В данном случае значения остатков приведены в таблице 4.2.
Таблица 4.2
| Семья | у | е | |
| 1 | 2 | 3 | 4 |
| 1,93 | 5,82 | - 3,90 | |
| 7,13 | 6,56 | 0,57 | |
| 8,78 | 7,29 | 1,49 | |
| 9,69 | 8,03 | 1,67 | |
| 10,09 | 8,76 | 1,33 |
Продолжение табл. 4.2.
| 1 | 2 | 3 | 4 |
| 10,42 | 9,50 | 0,93 | |
| 10,62 | 10,23 | 0,39 | |
| 10,71 | 10,97 | - 0,26 | |
| 10,79 | 11,70 | - 0,91 | |
| 11,13 | 12,43 | - 1,31 |
Положительные или отрицательные, большие или малые остатки должны чередоваться случайным образом. Здесь же, как видно из таблицы, сначала остатки отрицательны, затем они становятся положительными, достигают максимума, а потом снова уменьшаются и становятся отрицательными: это представляется сомнительным.
В данном примере соотношение имеет вид:
у = 12 - 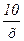 (4.8.)
(4.8.)
где х принимает целые значения от 1 до 10. Если мы знаем это и определим z = 1/ х, то уравнение примет линейный вид (4.7.) . Значение z для каждой семьи уже подсчитано в таблице 4.1. Оценив регрессию между y и z , получим
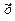 = 12, 08 - 10, 08 z ; R2 = 0, 9989
= 12, 08 - 10, 08 z ; R2 = 0, 9989
Стандартные ошибки (0, 04) (0,12 ) (4.9.) Подставив z = 1 / x , имеем
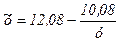 (4.10.)
(4.10.)
С учетом высокого качества оцененного уравнения (4.9.) неудивительно, что соотношение (4.10) близко к истинному уравнению (4.8 ) На слайде (рис. 4.3 и рис. 4.4) показаны регрессионная зависимость и точки наблюдений для у, х и z.
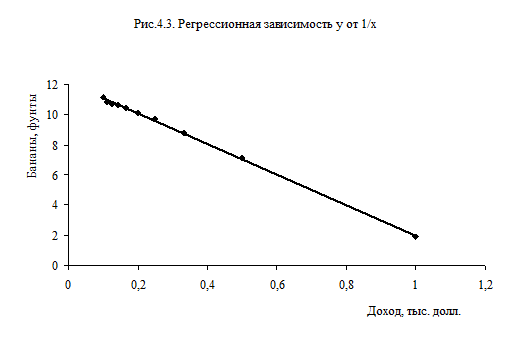 |
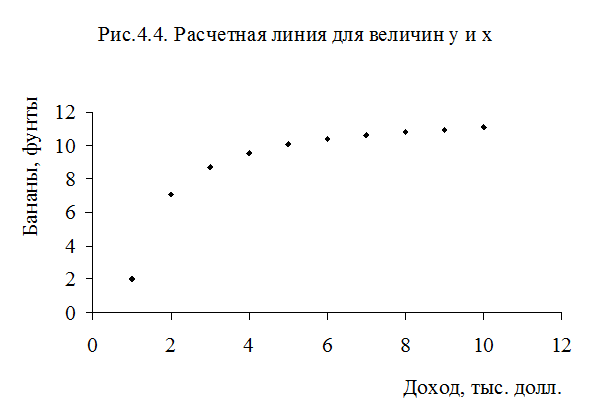
Улучшение качества уравнения, измеряемого с помощью коэффициента R2, отражено в более полном соответствии графиков. Сравните графики на рис.4.2. и 4.4.
Степенная функция.
Рассмотрим далее функции вида
у = aх b (4.11)
которые являются нелинейными как по параметрам, так и по переменным. Данное соотношение может быть преобразовано в линейное уравнение путем использования логарифмов, знакомых вам из курса математики. Ниже приведем основные свойства логарифмов, которые помогут вам в преобразованиях нелинейных уравнений.
Основные правила гласят :
1. Если у = х z , то log y = log x + log z .
2. Если y = x / z , то log y = log x - log z.
3. Если y = x n, то log y = n log x.
Эти правила могут применяться вместе для преобразования более сложных выражений. Например, если у = a х b , то по правилу 1 :
log y = log a + log x b и по правилу 3
= log a + b log x.
Если обозначить у1 = log (y) , z = log x и a 1 = log a , то уравнение (4.11) можно переписать в следующем виде:
у 1 = a1 + b z (4.12)
Процедура оценивания регрессии теперь будет следующей. Сначала вычислим у 1 и z для каждого наблюдения путем взятия логарифмов от исходных значений. Вы можете сделать это на компьютере с помощью имеющейся статистической программы. Затем оценим регрессионную зависимость у1 от z. Коэффициент при z будет представлять собой непосредственную оценку b. Постоянный член является оценкой a1, то есть log a. Для получения оценки a необходимо взять антилогарифм, то есть выполнить обратное действие.
Дата добавления: 2015-11-06; просмотров: 2209;
