Спецификация модели

Лекция 4. Нелинейная регрессия

Рассматриваемые вопросы

1. Спецификация модели

2. Классификация нелинейных функций

3. Отдельные виды нелинейных регрессий:

3.1. парабола;

3.2. равносторонняя гипербола;

3.3. степенная функция.

4. Коэффициенты эластичности в нелинейных регрессиях.

5. Корреляция для нелинейной регрессии.

Спецификация модели

Эконометрика как система специфических методов начала развиваться с осознания своей главной задачи – отражения связей экономических переменных. Многие экономические процессы наилучшим образом описываются нелинейными соотношениями, например, функциями спроса и производственными функциями. С этой целью в уравнение регрессии начали включаться переменные не только в первой, но и второй степени – с целью отразить свойства оптимальности экономических переменных, то есть наличия значений, при которых достигается минимальное или максимальное воздействие на зависимую переменную. Таково, например, влияние внесения удобрений на урожайность (до определенного уровня насыщение почвы удобрениями способствует росту урожайности, а по достижении оптимального уровня насыщение его дальнейшее наращивание может привести к снижению урожайности). То же можно сказать о воздействии многих социально-экономических переменных, например, влияния дохода на потребление некоторых продуктов питания. В условиях конкретной выборки данных нелинейность влияния переменных может и не подтвердиться, если эти данные варьируют в узких пределах, то есть являются однородными.

Предполагая, что ошибки измерения переменных сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели, то есть ошибкам, вызванным неверным видом уравнения регрессии.

В парной регрессии выбор вида математической функции, моделирующей связь переменных, может быть осуществлен тремя методами:

1) графическим;

2) аналитическим, то есть исходя из теории изучаемой взаимосвязи;

3) экспериментальным.

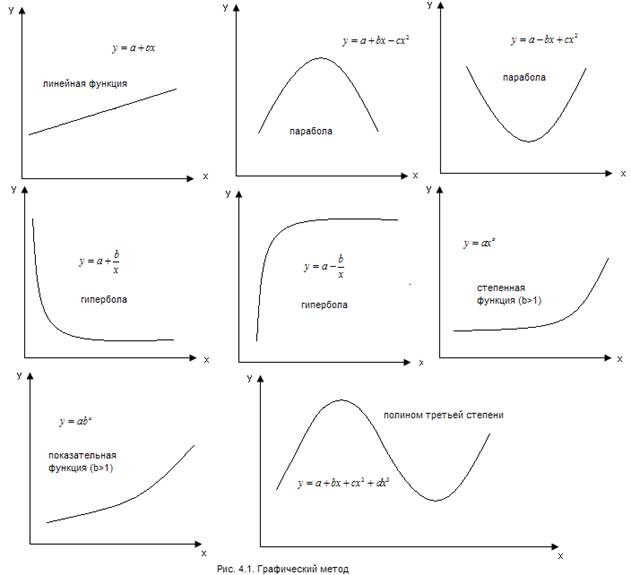
При изучении зависимости между двумя признаками наиболее наглядным является графический метод подбора уравнения. Он основан на построении поля корреляции. Основные типы кривых, используемых при количественной оценке связей, представлены на слайде (рис.4.1).

Класс математических функций для описания связи двух переменных достаточно широк. Кроме указанных, используются и другие типы кривых.

Значительный интерес представляетаналитический метод выбора типа уравнения регрессии. Он основан на изучении материальной природы связи исследуемых переменных. Пусть, например, изучается потребность предприятия в электроэнергии у в зависимости от объема выпускаемой продукции х. Все потребление электроэнергии можно подразделить на две части:

1) не связанное с производством продукции (а);

2) непосредственно связанное с объемом выпускаемой продукции, пропорционально возрастающее с увеличением объема выпуска (в*х) – слайд.

Тогда зависимость потребления электроэнергии от объема продукции можно выразить уравнением регрессии вида

у = а + вх. 4.1.

Если затем разделить обе части уравнения на величину объема выпуска продукции (х), то получим выражение зависимости удельного расхода электроэнергии на единицу продукции z = у/х от объема выпущенной продукции (х) в виде уравнения равносторонней гиперболы

z = в + а/х. 4.2.

Аналогично, текущие производственные затраты предприятия могут быть подразделены на условно-постоянные и условно-переменные, и тогда зависимость себестоимости единицы продукции от объемов производства также характеризуется равносторонней гиперболой.

Выбор вида уравнения регрессии экспериментальным методом обычно осуществляется при обработке информации на компьютере путем сравнения величины остаточной дисперсии, рассчитанной при разных моделях. Чем меньше величина остаточной дисперсии, тем в меньшей мере наблюдается влияние прочих, не учитываемых в уравнении регрессии факторов, тем лучше уравнение регрессии подходит к исходным данным.

Если остаточная дисперсия оказывается примерно одинаковой для нескольких функций, то на практике предпочтение отдается более простым видам функций, ибо они в лучшей степени поддаются интерпретации и требуют меньшего объема наблюдений. Число наблюдений должно в 6-7 раз превышать число рассчитываемых параметров при переменной х. Значит, если мы выбираем параболу второй степени

у = а + вх + сх² 4.3.

то требуется объем информации не менее 14 наблюдений. Учитывая, что эконометрические модели часто строятся по данным рядов динамики, ограниченным по протяженности (10, 20, 30 лет), то при выборе спецификации модели предпочтительнее модель с меньшим числом параметров при х.