Малюнок № 5. Множина розв’язків нерівностей х>а і х³а .

Твердження 2: множиною розв’язків нерівності х<а (х≤а) називається ліва півплощина, на які пряма х=а розбиває координатну площину (у випадку х≤а разом з прямою у=а).

Твердження 3: множиною розв’язків нерівності у>а (у≥а) є верхня із півплощин, на які пряма у=а розбиває координатну площину (у випадку у³а разом з прямою у=а).

Твердження 4: множиною розв’язків нерівності у<а (у≤а) є нижня півплощина, на які пряма у=а розбиває координатну площину (у випадку у≤а разом з прямою у=а).

Твердження 5: множиною розв’язків нерівності y<kx+b є нижня із півплощин, на які ця пряма розбиває координатну площину, без прямої y=kx+b.

Твердження 6: множиною розв’язків нерівності y>kx+b є верхня із півплощин, на які ця пряма розбиває координатну площину, без прямої y=kx+b.

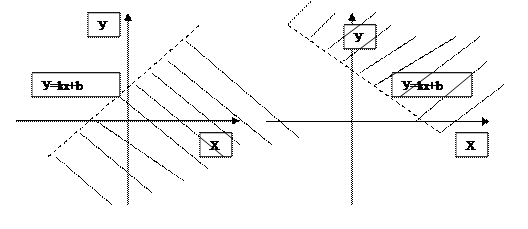
Малюнок № 6. Множина розв’язків нерівностей y<kx+b і y>kx+b.

Твердження 7: множиною розв’язків нерівності y≤kx+b є нижня із півплощин, на які пряма у=kx+b розбиває координатну площину, разом з прямою у=kx+b.

Твердження 8: множиною розв’язків нерівності y³kx+b є верхня із півплощин, на які пряма у=kx+b розбиває координатну площину, разом з прямою у=kx+b.

Твердження 9: множиною розв’язків нерівності (х-а)²+(у-b)²<R² є та частина координатної площини, яка знаходиться всередині кола з центром в точці (а,b) і радіусом R без точок кола (х-а)²+(у-b)²=R².

Твердження 10: множиною розв’язків нерівності (х-а)²+(у-b)²>R² є та частина координатної площини, яка знаходиться поза колом з центром в точці (а,b) і радіусом R без точок кола (х-а)²+(у-b)²=R².

Твердження 11: множиною розв’язків нерівності (х-а)²+(у-b)²≤R² є та частина координатної площини, яка знаходиться всередині кола з центром в точці (а,b) і радіусом R з точками кола (х-а)²+(у-b)²=R².

Твердження 12: множиною розв’язків нерівності (х-а)²+(у-b)²≥R² є та частина координатної площини, яка знаходиться поза колом з центром в точці (а,b) і радіусом R з точками кола (х-а)²+(у-b)²=R² .

Із розв’язанням систем і сукупностей нерівностей, досить часто доводиться зустрічатися при розв’язанні дробово-раціональних нерівностей та нерівностей, одна частина яких є добутком, а інша дорівнює 0. Покажемо це на конкретному прикладі.

Вправа: розв’язати нерівність: 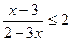, обґрунтовуючи виконувані дії теоремами про рівносильність нерівностей.

Розв’язання.

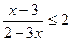Знайдемо область визначення нерівності. 2-3х≠0↔3х≠2↔х≠2/3. Із нерівності на основі теорем про рівносильність нерівностей маємо: ↔ ↔ . Звідси отримуємо таку сукупність систем нерівностей:

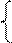7х-7≥0 7х≥7 х≥1 х≥1

2-3х<0 3х>2 х>2/3

7х-7≤0 7х≤7 х≤1

2-3х>0 3х<2 х<2/3 х<2/3.

Таким чином, множиною розв’язків заданої нерівності буде множина: (-∞;2/3)È[1;+∞).