Малюнок 19. Задання декартового добутку множин за допомогою графа.

Властивості 1-7 доводяться за допомогою міркувань. Покажемо це на прикладі останньої властивості. У першій частині доведемо, що кожен елемент лівої частини, яка складається із впорядкованих пар, належить правій частині. Нехай пара (х;у)ÎА´(В\С). Згідно означення декартового добутку це означає, що хÎА і уÎВ\С. Якщо уÎВ\С, то за означенням різниці множин уÎВ і уÏС. Оскільки хÎА і уÎВ, то за означенням декартового добутку множин (х,у)ÎА´В. Оскільки хÎА і уÏС, то (х,у)ÏА´С. Якщо (х,у)ÎА´В і (х,у)ÏА´С, то згідно з означенням операції різниці множин (х,у)Î(А´В)\(А´С), тобто правій частині. Пару (х,у) у лівій частині ми вибирали довільно, а тому наші міркування можна повторити відносно будь-якої пари, що належить лівій частині. Таким чином, множина А´(В\С) є підмножиною множини (А´В)\(А´С), тобто А´(В\С)Ì(А´В)\(А´С). Отже, першу частину доведено.

У другій частині доведемо, що кожен елемент правої частини є елементом лівої. Нехай пара (а;в)Î(А´В)\(А´С). Згідно означення різниці, (а;в)Î(А´В) і (а;в)Ï(А´С). Звідси аÎА і вÏС. Якщо (а;в)Î(А´В), то за означенням декартового добутку множин аÎА і вÎВ. Оскільки вÎВ і вÏС, то за означенням різниці множин вÎВ\С. Якщо аÎА і вÎВ\С, то за означенням декартового добутку множин (а;в)ÎА´(В\С), тобто лівій частині. Пару (а;в) у правій частині ми вибирали довільно, а тому наші міркування можна повторити відносно будь-якої пари, що належить правій частині. Таким чином, множина (А´В)\(А´С) є підмножиною множини А´(В\С), тобто (А´В)\(А´С)ÌА´(В\С). Отже, другу частину доведено.

Таким чином, у першій частині ми довели, що (А´(В\С))Ì((А´В)\(А´С)), а у другій – ((А´В)\(А´С))Ì(А´(В\С)). Звідси на основі означення рівності множин маємо рівність А´(В\С)=(А´В)\(А´С), тобто справедливість властивості доведено повністю.

Спробуємо знайти залежність, яка б допомогла шукати число елементів декартового добутку множин, якщо відомо число елементів вихідних множин. Нехай А={1, 2, 3} і В={а, в}. Утворимо множину А´В={(1;а ), (1;в), (2;в), (3;а), (3;в)}. Легко бачити, що n(А)=3, n(В)=2 і n(А´В)=6, тобто n(А´В)=n(А)·n(В). У математиці для загального випадку доведено теорему: „Число елементів декартового добутку множин А₁, А₂, А_3,... ,А_к, що мають відповідно n_1,n_2,n_3,...,n_kелементів дорівнює добутку чисельностей цих множин, тобто n(А₁´А₂´А₃´…´А_к)=n(А₁)n(А₂)n(А₃)…n(А_к)=n_1,n_2,n_3, ..., n_k”.

Як же визначити число елементів об’єднання двох скінченних множин? Для цього доведеться розглядати два випадки: 1) множини А і В не мають спільних множин, тобто АÇВ=Æ; 2) множини А і В мають спільні елементи, тобто АÇВ¹Æ. У першому випадку використовується формула n(АÈВ)=n(А)+n(В), а в другому - n(АÈВ)=n(А)+n(В)–n(АÈВ). Чи можна поширити ці формули на будь-яке число елементів? – математика дає на це ствердну відповідь, тобто справедлива формула: n(А₁ÈА₂ÈА₃È...ÈА_к)=n(А₁)+n(А₂)+n(А₃)+...+n(А_к), коли множини попарно не перетинаються.

МОДУЛЬ 1: «Множини. Відповідності Відношення.».

Змістовний модуль1.2. «Відповідності та відношення.».

ПЛАН.

1. Поняття відповідності між елементами двох множин, бінарні відповідності, їх позначення та способи задання. Множина відправлення та множина прибуття відповідності. Образи і прообрази елементів і множин, їх позначення.

2. Типи відповідностей (порожня, повна, всюди визначена у множині відправлення, сюр’єктивна, інє’ктивна, функціональна відповідність або функція, відображення, бієктивна). Обернені функції та відображення.

3. Бінарні відношення між елементами однієї множини, способи їхнього задання та їх властивості: рефлексивність, антирефлексивність, симетричність, асиметричність, антисиметричність, транзитивність, антитранзитивність.

4. Відношення еквівалентності та порядку, їх властивості. Впорядковані множини. Зв'язок відношення еквівалентності з розбиттям множини на класи, що попарно не перетинаються.

ЛІТЕРАТУРА

[1] –с. 3-40; [2] –с. 11-88; [3] –с. 5-56.

1. Теорія множин вивчає множини та операції над ними. Розглядаючи це не цікавляться, як правило, природою елементів, із яких складається множина, способом задання множин і порядком розміщення елементів у множині. Разом з тим, математична теорія завжди прагне знайти своє застосування до розв’язування практичних задач. Як же це відбувається з теорією множин? – її застосовують до побудови математичних теорій, до розв’язування практичних завдань, розглядаючи множини, між елементами яких існують ті чи інші відношення. Прикладом таких відношень у повсякденному житті є родинні відношення між людьми, відношення на роботі між колегами, в математиці – це відношення паралельності, подільності, рівності тощо.

Слід зазначити, що поняття відповідності, відношення розуміють майже однозначно. Однак таке розуміння носить інтуїтивний, а не точний характер. Для вивчення різноманітних відношень між математичними об’єктами інтуїтивне поняття «відношення» слід уточнити, але так, щоб воно набуло цілком конкретного математичного змісту і в той же час не втратило своєї інтуїтивної сутності. Розглянемо дві скінченні множини Х={2, 4, 6, 8} і У={2, 3}. Утворимо із елементів цих множин впорядковані пари так, щоб перша компонента пари ділилася націло на другу компоненту. Отже, матимемо таку множину пар А={(2;2), (4;2), (6;2), (8;2), (6;3)}. Утворимо тепер декартів добуток множин Х і У: Х×У={(2;2), (2;3), (4;2), (4;3), (6;2), (6;3), (8;2), (8;3)}. Що можна сказати про множини А і Х×У? – множина А є підмножиною множини Х×У, тобто АÌХ×У. Враховуючи це, можна ввести таке означення поняття відношення:

Означення: бінарним відношенням, визначеним між елементами множин Х і У, називається будь-яка підмножина декартового добутку цих множин Х і У.

Означення: відповідністю між множинами Х і У називається трійка множин Х, У і GÌХ×У.

Множину Х називають множиною відправлення або областю визначення відповідності, множину У – множиною прибуття або множиною значень відповідності, а множину впорядкованих пар GÌХ×У, які перебувають у відповідності, - графіком відповідності. Домовилися відповідності позначати малими буквами грецького алфавіту α, β, γ, δ, ε та ін. Символічний запис α={GÌХ×У} означає, що задано відповідність між елементами множин Х і У. Якщо елементи пари (х;у) перебувають у відповідності α, то це позначають так: хαу і читають «елемент у відповідає елементу х у відповідності α». Інколи відповідності позначають і великими буквами латинського алфавіту R, S, T, наприклад: хRу, аSв тощо. Слід зазначити, що уже в початкових класах діти знайомляться з відповідностями та відношеннями. Так, молодші школярі розглядають відношення рівності, більше, менше тощо.

Коли ж відповідність вважається заданою та які способи задання відповідностей існують? – тоді, коли відносно будь-якої пари можна сказати належить чи не належить вона відповідності. Оскільки відповідність є підмножиною декартового добутку множин, то цілком логічно припустити, що відповідності можна задати всіма тими способами, якими задавався декартів добуток множин, а саме: 1) переліком всіх пар елементів, які перебувають у цій відповідності; 2) за допомогою характеристичної властивості; 3) таблицею; 4) рівнянням; 5) графіком; 6) графом. Не всі вказані способи задання відповідностей рівнозначні, а найзручнішим буде той, який потрібен саме для конкретної відповідності (пропонуємо виконати завдання № 38 для самостійної роботи!).

Отже, виникає запитання «чи однакові всі відповідності та як виділяти в них різні типи?». Перед тим, як знайти відповіді на ці запитання, розглянемо питання про образи та прообрази елементів у відповідності.

Означення: образом елемента аєА у відповідності αÌА×В називають множину тих елементів вєВ, для яких (а;в)єα.

Означення: прообразом елемента вєВ у відповідності αÌА×В називають множину тих елементів аєА, для яких (а;в)єα.

Домовилися образ елемента аєА у відповідності αÌА×В позначати α(а). Прообраз елемента вєВ при цій же відповідності αÌА×В будемо позначати так: α^-1(а). Нехай відповідність задана графом (див. малюнок № 20).

Малюнок 20. Граф відповідності.

Користуючись малюнком, знайдемо образи і прообрази елементів, які перебувають у відповідності, заданій графом. α(1)={4, 8}, α(2)=Ø, α(3)={2, 4}, α(4)={2, 6, 8}, α(5)={4}, α^-1(2)={2, 3, 4}, α^-1(4)={2, 4, 5}, α^-1(6)= Ø, α^-1(8)={1, 4}. Із наведеного прикладу видно, що не всі елементи множини А мають образи у множині В. Так само як і не всі елементи множини В мають прообрази у множині А. враховуючи попереднє зауваження із базових множин А і В можна виділити дві підмножини: 1) підмножину α(А)={в/вєВ і існує таке аєА, що аαв}. Її називають множиною значень відповідності α і позначають α(А)ÌВ; 2) підмножину α^-1(В)={а/аєА і існує таке вєВ, що аαв}. Цю множину називають областю визначення відповідності α і позначають α^-1(В)ÌА. Таким чином, множина значень відповідності α(А) є об’єднанням образів всіх елементів множини А, а область визначення відповідності α^-1(В) є об’єднанням прообразів усіх елементів множини В.

2. Яке співвідношення може існувати між множинами G і Х×У? – 1) G∩Х×У=Ø; 2) GÌХ×У; 3) G=Х×У. Виходячи із цих співвідношень можна виділити наступні характерні типи відповідностей:

1) порожня відповідність, при якій G∩Х×У=Ø і α= Ø;

2) повна відповідність, при якій α=Х×У і у графі якої від кожного елемента множини Х йдуть стрілки до кожного елемента множини У;

3) відповідність всюди визначена у множині відправлення Х, тобто така, у якої GÌХ×У і для якої α^-1(У)=Х. Це означає, що всі елементи множини Х мають образи у множині У. На графі такої відповідності із кожного елемента множини Х виходить стрілка до якогось елемента множини У;

4) сюр’єктивна відповідність, тобто відповідність на всю множину прибуття У, причому α(Х)=У. При такій відповідності кожен елемент множини У має прообраз у множині Х. Для графа цієї відповідності характерно те, що із кожного елемента множини Х виходить стрілка і в кожен елемент множини У входить стрілка;

5) інє’ктивна відповідність – це така відповідність αÌХ×У, у якої прообрази елементів з множини У містять не більше одного елемента з множини Х. На графі такої відповідності в елементи множини У входить не більше однієї (одна або жодної) стрілки;

6) функціональна відповідність або функція, при якій образи елементів з множини Х або порожні, або містять лише один елемент. Граф цієї відповідності характеризується тим, що з кожного елемента множини Х виходить або одна стрілка, або не виходить жодної стрілки, але в елементи множини У може входити більше, ніж одна стрілка;

7) відображення – це всюди визначена функціональна відповідність, коли кожному елементу з множини Х відповідає єдиний елемент у множині У. Такі відповідності, тобто відображення, у свою чергу, поділяють на дві групи: а) відображення множини Х в множину У, коли у множині У є елементи, які не мають прообразів в множині Х. Граф такого відображення характеризується тим, що з всіх елементів множини Х виходять стрілки, але не в кожен елемент множини У входить хоча б одна стрілка; б) відображення множини Х на множину У, коли кожен елемент з множини У має прообраз у множині Х;

8) бієктивна або взаємно однозначна відповідність, яка одночасно всюди визначена, сюр’єктивна, інє’ктивна та функціональна, тобто це ін’єктивне та сюр’єктивне відображення.

У математиці доволі часто доводиться мати справу з оберненими об’єктами (обернені числа, обернені задачі, обернені теореми, обернені функції тощо). Отже, цілком доцільним є введення понять оберненої відповідності та оберненого відображення.

Означення: відповідністю, оберненою до відповідності αÌХ×У, називається така відповідність α^-1, яка є підмножиною декартового добутку множин У×Х і складається з тих і тільки тих пар (у;х), для яких (х;у)єα.

Якщо взяти функціональну відповідність і побудувати для неї обернену, то відповідь на запитання «чи буде одержана відповідність функціональною?» не завжди позитивна.

Означення: відображенням, оберненим до даного відображення f, називається таке відображення f^-1, у якого для кожного хєХ і уєУ, якщо f(х)=у, то f^-1(у)=х, тобто f^-1(f(х))=х.

У математиці доведено теорему, яка дає відповідь на запитання «які відображення мають обернені?».

Теорема: відображення fÌХ×У має обернене відображення f^-1 тоді і тільки тоді, коли відображення f – бієктивне.

Цю теорему приймемо без доведення.

Означення: відображення f називається оборотним, якщо воно має обернене відображення f^-1.

3. Хоча поняття відповідності та відношення досить близькі, але вони мають суттєві відмінності. Не зупиняючись на цих відмінностях, які не є предметом нашого розгляду, приймемо наступне означення.

Означення: якщо у відповідності f множина відправлення Х співпадає з множиною прибуття У, то таку відповідність будемо називати відношенням між елементами множини Х.

Означення: бінарним відношенням, визначеним у множині Х, називається кожна підмножина декартового квадрату Х×Х=Х².

Як же можна задавати відношення? – оскільки відношення це відповідність, то його можна задавати тими самими способами, тобто за допомогою переліку, характеристичної властивості, таблиць, графів, графіків, формулою (аналітично). Які ж є типи відношень? – залежно від набору певних властивостей виділяють типи відношень, які ми визначимо за допомогою наступних означень.

Означення: відношення α, визначене у множині Х, називається рефлексивним, якщо кожний елемент множини Х перебуває у відношенні α сам з собою, тобто аαа.

Символічно наведене означення можна записати так: ( 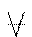хєХ)(аαа). Якщо відношення α рефлексивне, то говорять, що елементи множини Х мають властивість рефлексивності. Прикладами рефлексивних відношень є відношення подільності на множині чисел (а:а), рівності на множині фігур, паралельності на множині площин тощо.

Означення: відношення α, визначене у множині Х, називається антирефлексивним, якщо не кожен елемент множини Х перебуває у відношенні α сам з собою, тобто аαа.

Символічно наведене означення можна записати так: ( 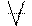хєХ)(аαа). Якщо відношення α антирефлексивне, то говорять, що елементи множини Х мають властивість антирефлексивності. Прикладами антирефлексивних відношень є відношення більше на множині чисел, перпендикулярності на множині прямих тощо.

Означення: відношення α, визначене у множині Х, називається симетричним, якщо для будь-яких а,вєХ із того, що аαв→вαа.

Символічно наведене означення можна записати так: ( 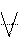а,вєХ)(аαв→вαа). Якщо відношення α симетричне, то говорять, що елементи множини Х мають властивість симетричності. Прикладами симетричних відношень є відношення дорівнює на множині фігур, перпендикулярності на множині прямих тощо.

Означення: відношення α, визначене у множині Х, називається асиметричним, якщо для будь-яких а,вєХ із того, що аαв→вαа.

Символічно наведене означення можна записати так: ( 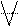а,вєХ)(аαв→вαа). Якщо відношення α асиметричне, то говорять, що елементи множини Х мають властивість асиметричності.

Означення: відношення α, визначене у множині Х, називається антисиметричним, якщо для будь-яких а,вєХ із того, що (аαв^вαа)→(а=в).

Символічно наведене означення можна записати так:

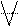( а,вєХ)(аαв^вαа)→(а=в). Якщо відношення α антисиметричне, то говорять, що елементи множини Х мають властивість антисиметричності.

Означення: відношення α, визначене у множині Х, називається транзитивним, якщо для будь-яких а,в,сєХ із того, що (аαв^вαс)→(аαс).

Символічно наведене означення можна записати так:

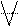( а,в,сєХ)(аαв^вαс)→(аαс). Якщо відношення α транзитивне, то говорять, що елементи множини Х мають властивість транзитивності. Прикладами транзитивних відношень можуть бути: відношення подільності на множині чисел, відношення менше на множині кутів тощо.

Означення: відношення α, визначене у множині Х, називається антитранзитивним, якщо для будь-яких а,в,сєХ із того, що (аαв^вαс)→(аαс).

Символічно наведене означення можна записати так:

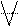( а,в,сєХ)(аαв^вαс)→(аαс). Якщо відношення α антитранзитивне, то говорять, що елементи множини Х мають властивість антитранзитивності.

Означення: відношення α, визначене у множині Х називається зв’язним, якщо для будь-яких аαв і а≠в випливає, що аαв або вαа.

Прикладом таких відношень є відношення більше, менше на множині чисел.

4. Як можна було б згрупувати різні за змістом відношення? – навколо певних наборів властивостей. У математиці відношення між елементами однієї множини поділяють принаймні на три групи: 1) відношення еквівалентності; 2) відношення порядку; 3) функціональні відношення. Розглянемо перші дві групи.

Означення: будь-яке рефлексивне, симетричне та транзитивне відношення f, визначене у множині Х, називається відношенням еквівалентності.

Прикладами відношень еквівалентності є відношення подібності на множині трикутників, паралельності на множині площин, «бути однокурсником» на множині студентів тощо. Як визначити, чи є задане відношення відношенням еквівалентності? – перевірити наявність у нього властивостей, які повинні бути у відношення такого типу. Покажемо це на конкретному прикладі.

Вправа: з’ясувати, чи є відношенням еквівалентності відношення «проживати на одній вулиці», задане на множині людей.

1) оскільки кожна людина проживає на одній вулиці сама з собою, то це відношення рефлексивне;

2) якщо людина А проживає на одній вулиці з людиною В, то і людина В проживає на одній вулиці з людиною А, тобто із (АαВ)→(ВαА);

3) якщо людина А проживає на одній вулиці з людиною В, а людина В проживає на одній вулиці з людиною С, то і людина А проживає на одній вулиці з людиною С, тобто із ((АαВ)^(ВαС))→(АαC).

Отже, відношення α:«проживати на одній вулиці», задане на множині людей, є рефлексивним, симетричним і транзитивним, а тому відноситься до відношень типу еквівалентності.

Розглядаючи поняття розбиття множини на підмножини, що попарно не перетинаються, ми з’ясували, що відношення «бути однокурсником» на множині студентів, розбило множину всіх студентів на п’ять підмножин. З’ясуємо властивості цього відношення. Легко бачити, що воно має властивості рефлексивності, симетричності і транзитивності (Чому?), а тому є відношенням типу еквівалентності. Сказане дає підстави припустити, що між розбиттям множини на класи, що попарно не перетинаються, і відношеннями типу еквівалентності існує певний зв'язок. Сутність цього зв’язку розкривається такою теоремою.

Теорема: для того, щоб відношення α дозволяло розбити множину Х на класи, що попарно не перетинаються, необхідно і достатньо, щоб відношення α було відношенням еквівалентності.

Оскільки у формулюванні цієї теореми є слова необхідно і достатньо, то доведення теореми складається із двох частин: 1) із доведення необхідності; 2) із доведення достатності. Цю теорему приймемо без доведення.

Означення: бінарне відношення α, визначене у множині Х, називається відношенням строгого порядку, якщо воно антирефлексивне, антисиметричне і транзитивне.

Прикладами відношень строгого порядку є: відношення «менше» у множині цілих чисел; відношення «бути старшим» на множині людей; відношення «бути вищим» на множині дерев тощо.

Означення: бінарне відношення α, визначене у множині Х, називається відношенням нестрогого порядку, якщо воно рефлексивне, антисиметричне і транзитивне.

Прикладами відношень нестрогого порядку є: відношення «більше або дорівнює» у множині раціональних чисел; відношення подільності на множині натуральних чисел тощо.

Означення: відношення порядку в множині Х називається відношенням лінійного порядку, якщо для будь-яких елементів х,уєХ виконується умова хαу٧уαх. Якщо ж відношення не має такої властивості, то його називають відношенням часткового порядку.

Прикладом відношення лінійного порядку є відношення «більше» чи «менше» на множині чисел.

Означення: якщо відношення α в множині Х є відношенням часткового порядку, то множину Х називають частково впорядкованою множиною.

Означення: якщо відношення α в множині Х є відношенням лінійного порядку, то множину Х називають лінійно впорядкованою множиною.

Лінійно впорядковані множини мають ряд властивостей. Нехай а,в,сєХ і множина Х лінійно впорядкована відношенням α. Якщо відомо, що аαв^вαс, то говорять, що елемент в лежить між елементами а і с.

Означення: множина Х, яка лінійно впорядкована відношенням α, називається дискретною, якщо між будь-якими двома її елементами знаходиться лише скінченна множина елементів.

Прикладом дискретних множин є множини натуральних і цілих чисел.

Означення: множина Х, яка лінійно впорядкована відношенням α, називається щільною в собі, якщо для будь-яких двох різних її елементів існує елемент цієї множини, що лежить між ними.

Прикладом щільних в собі множин є множина дійсних чисел.

МОДУЛЬ 1: «Множини. Відповідності Відношення.».

Змістовний модуль1.3. «Елементи комбінаторики».

План.

1. Комбiнаторнi задачі. Правила суми i добутку.

2. Розміщення з повтореннями та без повторень.

<123 4 5 6 7 >

Дата добавления: 2015-11-04; просмотров: 2109;