Перестановки з повтореннями та без повторення. 4 страница
1. аÚ`а=1 – закон виключеного третього.
2. а Ù`а = 0 – закони несуперечливості
а Ù `а = 1
Запитання для самоконтролю та самостійної роботи студентів за змістовним модулем 2.2.
1. Запишіть довільне висловлення та утворіть його заперечення двома способами.
2. Довести справедливість закону подвійного заперечення висловлень, побудувавши таблицю істинності.
3. Довести справедливість закону подвійного заперечення предикатів, побудувавши таблицю істинності.
4. Довести, побудувавши таблицю істинності, комутативний закон операції кон’юнкції, а саме: аÙв=вÙа.
5. Записати закони операції кон’юнкції предикатів, використавши закони операції кон’юнкції висловлень.
6. Самостійно довести, побудувавши таблиці істинності, комунікативний, асоціативний, два дистрибутивні та перший закон де Моргана.
7. Записати самостійно закони, яким підкоряється операція диз’юнкції предикатів.
 8. Пропонуємо студентам довести обидві формули (1) а↔b=(а→b)Ù(b→а); 2) а↔b=(āÚb)Ù(bÚа)), побудувавши таблиці істинності (див. завдання для самостійної роботи).
8. Пропонуємо студентам довести обидві формули (1) а↔b=(а→b)Ù(b→а); 2) а↔b=(āÚb)Ù(bÚа)), побудувавши таблиці істинності (див. завдання для самостійної роботи).
9. Довести самостійно, побудувавши таблицю істинності, закон виключеного третього та закони несуперечливості.
МОДУЛЬ 2: «Висловлення. Предикати. Теореми.».
Змістовний модуль 2.3. «Теореми.».
ПЛАН.
1. Поняття теореми, її будова. Види теорем (дана, обернена, протилежна, обернена до протилежної, спряжені теореми) та зв'язок між ними.
2. Способи доведення теорем (дедуктивний, індуктивний, метод від супротивного тощо).
3. Необхідні та достатні умови.
4. Поняття міркування, правильні та неправильні міркування. Перевірка правильності міркувань з допомогою кругів Л.Ейлера.
5*. Алгоритми. Основні властивості алгоритмів. Приклади алгоритмів, що використовуються в курсі математики початкової школи.
Література.
[1] – с. 51-92. [2] – с. 3-11, 96-126. [3] – с. 79-168.
1. Поняття теореми, її будова. Види теорем (дана, обернена, протилежна, обернена до протилежної, спряжені теореми) та зв'язок між ними.
1. Вивчення будь-якого розділу математики супроводжується доведенням тверджень, серед яких істотну роль відіграють теореми, тобто твердження, в справедливості яких потрібно переконатися шляхом доведення. В шкільному курсі математики вивчаються теореми, які мають різноманітну форму запису. Для того, щоб успішно формувати у школярів уявлення про теорему та способи її доведення, необхідно знати форми запису, будову та види теорем. Ці знання ґрунтуються на поняттях висловлення та операцій над ними, предикатів та кванторів. Якщо проаналізувати більшість теорем, то можна помітити, що вони складаються з таких структурних компонентів: 1) пояснювальна частина, в якій роз’яснюється, для яких об’єктів доводиться теорема; 2) умова теореми, в якій вказується на ті поняття, що використовуються в теоремі, та яка може мати різноманітну структуру (бути простим висловленням; бути кон’юнкцією, диз’юнкцією, запереченням тощо кількох висловлень); 3) висновок теореми. Дуже часто теореми формулюють в імплікативній формі, коли пояснювальна частина символічно зображається у формі квантора загальності чи існування, а умова і висновок – у вигляді предикатів. Зазначимо, що при словесному формулюванні теореми, її пояснювальна частина не завжди формулюється явно, але її можна виділити. Наприклад, у формулюванні теореми «якщо точка лежить на перпендикулярі до середини відрізка, то вона рівновіддалена від кінців цього відрізка» пояснювальна частина «кожна точка перпендикуляра до середини відрізка» не сформульована явно.
Як правило, в теоремі присутні як мінімум два предикати, один із яких виражає умову теореми, а інший – висновок. Предикати, які виражають умову чи висновок, можуть бути складеними. Пояснювальна частина теореми символічно може записуватися у вигляді кванторів існування чи загальності. Проілюструємо це на прикладі такої теореми «для будь-яких дійсних чисел а, b, с, якщо а>в і b>с , то а>с». У цій теоремі пояснювальна частина буде такою «для будь-яких дійсних чисел», а тому символічно її можна записати так: ("а,b,сєR). Умовою теореми буде кон’юнкція предикатів (а>bÙb>с), а висновком теореми – предикат а>с. Отже, символічно теорема запишеться так: ("а,b,сєR)((а>bÙb>с)→(а>с)). Таким чином, умова теореми є складеним предикатом (кон’юнкцією двох предикатів), а висновок теореми є простий предикат. У пояснювальній частині можуть бути одночасно представлені квантори існування і загальності. Наприклад: для будь–яких двох дійсних чисел a та b існує єдине число с, таке, що а-в=с.



 Оскільки практично кожну теорему можна представити у вигляді імплікації двох предикатів, то, пригадуючи операцію імплікації предикатів, зазначимо, що є чотири види імплікацій. Саме тому можна твердити, що можна виділити чотири види теорем: 1) дана або пряма теорема, яку символічно можна записати так: А(х)→В(х); 2) обернена теорема, яку символічно можна записати так: В(х)→А(х); 3) протилежна теорема, яку символічно записують так: А(х)→В(х); 4) протилежна до оберненої або обернена до протилежної, яку символічно записують так: В(х)→А(х).
Оскільки практично кожну теорему можна представити у вигляді імплікації двох предикатів, то, пригадуючи операцію імплікації предикатів, зазначимо, що є чотири види імплікацій. Саме тому можна твердити, що можна виділити чотири види теорем: 1) дана або пряма теорема, яку символічно можна записати так: А(х)→В(х); 2) обернена теорема, яку символічно можна записати так: В(х)→А(х); 3) протилежна теорема, яку символічно записують так: А(х)→В(х); 4) протилежна до оберненої або обернена до протилежної, яку символічно записують так: В(х)→А(х).



 Розглядаючи імплікацію висловлень і предикатів, за допомогою побудови таблиці істинності ми довели, що серед чотирьох видів імплікацій є дві пари рівносильних, а саме: 1) (А(х)→В(х))≡(В(х)→А(х)); 2) (В(х)→А(х))≡(А(х)→В(х)). Із цих рівностей випливає, що не потрібно доводити всі чотири теореми, а слід довести лише дві, тобто по одній з кожної пари. Причому в математиці доводять з кожної пари ту теорему, яку легше довести.
Розглядаючи імплікацію висловлень і предикатів, за допомогою побудови таблиці істинності ми довели, що серед чотирьох видів імплікацій є дві пари рівносильних, а саме: 1) (А(х)→В(х))≡(В(х)→А(х)); 2) (В(х)→А(х))≡(А(х)→В(х)). Із цих рівностей випливає, що не потрібно доводити всі чотири теореми, а слід довести лише дві, тобто по одній з кожної пари. Причому в математиці доводять з кожної пари ту теорему, яку легше довести.
Розглянемо способи утворення вказаних видів теорем на прикладі наступної «якщо один із співмножників добутку дорівнює нулю, то добуток дорівнює нулю» - дана теорема, яка істинна. Щоб утворити теорему, обернену до даної поміняємо місцями умову і висновок. Одержимо теорему «якщо добуток двох співмножників дорівнює нулю, то один із співмножників добутку дорівнює нулю» - обернена теорема, яка хибна, бо нулю можуть дорівнювати обидва співмножники. Щоб сформулювати протилежна теорему, слід заперечити умову та висновок даної теореми. В цьому випадку отримуємо «якщо жоден із співмножників не дорівнює нулю, то добуток не дорівнює нулю» - протилежна теорема, яка істинна. Сформулюємо четверту теорему «якщо добуток не дорівнює нулю, то жоден із співмножників не дорівнює нулю» - протилежна до оберненої чи обернена до протилежної, яка істинна.
2. Способи доведення теорем (дедуктивний, індуктивний, метод від супротивного тощо).
2. Спочатку зазначимо, що довести теорему – це означає встановити логічним шляхом, що завжди, коли виконується властивість А(х) буде виконуватись і властивість В(х). Доведення теорем в математиці проводиться за правилом логіки без будь-яких посилань на наочність та досвід. У математиці існують різні способи доведення теорем, які класифікують по-різному. Серед різних способів доведення теорем зупинимося на характеристиці тих, які найчастіше зустрічаються в шкільному курсі математики. У першу чергу вкажемо на дедуктивний спосіб доведення теорем, сутність якого полягає в тому, що виходячи з умови теореми і використовуючи доведені раніше теореми, ми будуємо ланцюжок міркувань, який дозволяє нам переконатися в справедливості висновків теорем. Покажемо це на прикладі такої теореми «Сума внутрішніх кутів довільного трикутника дорівнює 180°».
Доведення: беремо довільний трикутник (див. малюнок №27) і проводимо через його вершину пряму, паралельну протилежній стороні (це можна зробити, оскільки доведено, що через точку, поза прямою можна провести пряму, паралельну даній). <1+<2+<3=180°, як сума кутів, які утворюють розгорнутий кут. <1=<4 – як внутрішні різносторонні при паралельних прямих та січній. Аналогічно <3=<5. Тоді рівність <1+<2+<3=180° перетвориться у рівність <4+<2+<5=180°. Отже, сума внутрішніх кутів трикутника дорівнює 180°. Теорему доведено.

Малюнок № 27.
Сутність індуктивних доведень полягає в тому, що на основі розглянутих кількох окремих випадків ми робимо загальний висновок. Для того, щоб не розглядати всі часткові випадки, в математиці є метод доведення, який називається методом математичної індукції. Він складається з таких етапів: а) перевіряємо твердження для n=1; б) припускаємо істинність твердження при n=k; в) виходячи з припущення пробуємо довести істинність твердження при n=k+1. Тоді дане твердження буде справедливим для будь-якого натурального числа. Проілюструємо сказане на такому прикладі: довести, що добуток двох послідовних натуральних чисел ділиться націло на 2.
Доведення:
1. Перевіримо справедливість твердження для будь-якої пари послідовних натуральних чисел. Дійсно, добуток 1•2=2, а 2 кратне 2. Отже, для n=1 і n=2 твердження справедливе.
2. Припустимо, що твердження справедливе для будь-якої пари послідовних натуральних чисел n і n+1, тобто n(n+1) 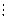 2.
2.
3. Спробуємо довести справедливість твердження для n=k+1. Утворимо добуток (n+1)(n+2) і розкриємо другу дужку. Отримуємо (n+1)n+2(n+1). У цій сумі перший доданок (n+1)n ділиться націло на 2 згідно припущення, а другий доданок 2(n+1) ділиться націло на 2 згідно теореми про подільність добутку. Таким чином, кожен доданок суми ділиться на 2, а тому і сума (n+1)n+2(n+1)=(n+1)(n+2) поділиться націло на 2. Отже, теорему доведено.
Наступним способом доведень є спосіб доведення від супротивного, сутність якого полягає в тому, що ми заперечуємо висновок теореми і пробуємо це довести. В результаті ми приходимо до суперечності із умовою теореми або з доведеним раніше твердженням. Найбільш часто цей спосіб доведення використовують при доведенні теорем єдиності. Покажемо це на такому прикладі: якщо різниця двох дійсних чисел існує, то вона єдина.
Доведення: нехай нам дано два дійсних числа а,вєR. Згідно означення різниці число а-в=сєR. Припустимо, що різниця двох дійсних чисел не єдина. Нехай існують дві різних різниці, тобто: а-b=с1 і а-b=с2, причому с1≠с2. Звідси маємо а=b+с1 і а=b+с2, тобто b+с1=b+с2, а тепер с1=с2, що суперечить вибору чисел с1 і с2. Ця суперечність говорить, що наше припущення про неєдиність різниці було хибним. Таким чином, якщо різниця існує, то вона єдина. Теорему доведено.
3. Необхідні та достатні умови.
3. Розглядаючи імплікацію предикатів, ми зазначали: якщо ("хєХ)(А(х)→В(х))=1, то предикат В(х) називають необхідною умовою для істинності предикати А(х), а предикат А(х) називають достатньою умовою для істинності предиката В(х). Якщо ж ("хєХ)(В(х)→А(х))=1, то предикат А(х) - необхідна умова для істинності предиката В(х), а предикат В(х) буде достатньою умовою для істинності предиката А(х). Якщо ж ("хєХ)(А(х)→В(х))=1 і ("хєХ)(В(х)→А(х))=1, то кожен із предикатів є необхідною і достатньою умовою для істинності іншого.
Будь-яку теорему можна сформулювати з використанням слів “необхідно”, “достатньо” чи “необхідно і достатньо”. Покажемо це на прикладі наступної теореми “якщо в чотирикутнику сторони попарно паралельні, то цей чотирикутник паралелограм”. У цій теоремі ми маємо два предикати: А(х): “у чотирикутнику х протилежні сторони попарно паралельні” і “В(х): “чотирикутник х – паралелограм”. Розглянемо імплікацію предикатів А(х)→В(х). Легко переконатися, що вона завжди істинна. Аналогічно імплікація В(х)→А(х)=1. Тоді кожний із предикатів є необхідною і достатньою умовою для іншого, а тому теорему сформулюємо так: “для того, щоб чотирикутник був паралелограмом, необхідно і достатньо, щоб його протилежні сторони були парно паралельні”. Як відомо, теореми, в яких використовують слова “необхідно і достатньо” називають ознаками, бо вони дозволяють з’ясувати, чи відносяться дані об’єкти до певного класу (наприклад, ознаки подільності, ознаки перпендикулярності тощо).
4. Поняття міркування, правильні та неправильні міркування. Перевірка правильності міркувань з допомогою кругів Л.Ейлера.
4. У своїй практичній діяльності людина спирається на закони природи та суспільства. Знання про них вона одержує, в основному, трьома способами: 1) спостерігаючи явища та речі в природних умовах і накопичуючи завдяки цьому відомості про оточуючий світ; 2) проводячи експерименти у штучностворених нею умовах; 3) міркуючи та одержуючи в результаті цих міркувань нові знання із відомих раніше. Вказані три способи є джерелами науки. Співвідношення трьох основних джерел в різних науках різне. У зв’язку з цим прийнято розрізняти описові, дослідні (експериментальні або емпіричні) та дедуктивні науки. До описових наук відносять комплекс географічних наук, зоологію, до експериментальних – фізику, хімію, до дедуктивних – математику, логіку.
Зазначимо, що такий поділ на вказані види наук досить відносний, бо в ході їх розвитку співвідношення між спостереженнями, експериментом і міркуваннями змінюється. У наш час спостерігається проникнення логічних і математичних методів в розділи наук, які вважалися у недалекому минулому описовими, наприклад, в біологію, економіку, лінгвістику тощо. У дедуктивних науках основним методом досліджень вважається виведення наслідків із невеликої кількості вихідних положень. Вони, як правило, є результатом досвіду та спостережень. Зміст і форма дедуктивних наук характеризується, головним чином, тим багатством наслідків, які можна та які одержані за допомогою міркувань.
Будь-яке міркування складається із ланцюжка висловлень, які випливають один з одного за певними правилами. Вміння міркувати, правильно обґрунтовувати свої висновки необхідне людині будь-якої професії. Людина вчиться міркувати, починаючи з того моменту, коли вона починає говорити. Разом з тим, цілеспрямоване навчання логіці міркувань починається в школі. Вже при вивченні курсу математики початкових класів учні розвивають уміння аналізувати, порівнювати, класифікувати, обґрунтовувати найпростіші твердження тощо. Саме тому вчитель початкових класів повинен бути обізнаним з наукою про закони і форми мислення, про загальні схеми міркувань. Основні типи суджень і умовиводів, що лежать в основі міркувань, розглядаються в класичній логіці, засновником якої вважається філософ стародавньої Греції Аристотель (384-422 рр. до н. е.).
В основі обґрунтування та доведення лежать міркування, під якими розуміють логічну операцію, в результаті якої із одного або декількох взаємопов’язаних за змістом речень одержують речення, що містить нове по відношенню до вихідних знання. Якщо проаналізувати структуру міркування, то можна помітити, що будь-яке з них складається із умови (або посилок) та висновку. Розглянемо міркування: якщо число просте, то воно має два дільники. В ньому посилкою є “якщо число просте”, а висновком - “то воно має два дільники”. Всі міркування можна поділити на дві великі групи: 1) дедуктивні міркування, в яких між посилкою і висновком має місце відношення слідування; 2) індуктивні міркування, в яких на підставі того, що деякі об’єкти множини мають певні властивості, робиться висновок про те, що цю властивість мають всі об’єкти цієї множини. Прикладом дедуктивного міркування може бути таке “якщо число кратне 8, то воно кратне 2“, а індуктивного - “2 кратне 2, бо закінчується 2, 4 кратне 4 бо закінчується 4. Отже, всі числа, які закінчуються на 2 і 4 діляться на 2”. Якщо дедуктивні міркування будуються за правилами логіки, то ми повинні з правильної посилки одержати правильний висновок. Для індуктивних міркувань цього сказати не можна.
Процес мислення має надзвичайно складний характер і відбувається у переплетінні тисячоліттями відшліфованих строгих форм утворення умовиводів, поки що не вивчених інтуїтивних уявлень і творчих актів, певних емоційних сторін діяльності вищої нервової системи людини тощо. Проте, ще стародавні мислителі відзначали, що істотна частина наших умовиводів робиться за певними стандартними схемами, які не залежать від того конкретного матеріалу, що ми ними оперуємо. Внаслідок вивчення цього процесу людського мислення виникла наука, яка одержала назву «формальна логіка». Вона займається вивченням способів утворення правильних висновків, виходячи з певних зв’язків між формою, структурою посилок або умов, а не з їхнього конкретного змісту.
Розглянемо кілька міркувань та з’ясуємо, як вони побудовані: 1) «якщо всі птахи - тварини і всі горобці - птахи, то всі горобці - тварини»; 2) «якщо всі птахи – тварини і всі квіти – птахи, то всі квіти - тварини»; 3) «якщо деякі французи – блондини і дехто з курців – французи, то деякі курці - блондини»; 4) «якщо деякі опуклі фігури – круги і деякі опуклі фігури – многокутники, то деякі многокутники - круги». Кожне з наведених міркувань складається з трьох висловлень. У перших двох прикладах у першому висловленні стверджується, що всі предмети деякого класу мають деяку властивість, яка є істотною для всіх предметів цього класу, а у другому висловленні стверджується, що всі предмети цього ж класу є частковим випадком більш загального поняття. У третьому та четвертому прикладах у першому висловлення стверджується, що деякі предмети мають певну властивість, яка є істотною для всіх предметів цього класу, а в другому висловленні цих прикладів стверджується, що деякі предмети є частковим випадком більш загального поняття. На цій основі робиться висновок про те, що відзначена властивість належить або всім, або деяким поняттям. Загальну форму цього міркування для перших двох прикладів можна представити так: «якщо всі предмети класу А мають властивість α і обсяг класу В є частиною обсягу класу А, то всі об’єкти класу В мають властивість α». Загальну форму цього міркування для двох останніх прикладів можна представити так: «якщо деякі предмети класу А мають властивість α і обсяг класу В є частиною обсягу класу А, то деякі об’єкти класу В мають властивість α». Міркування такого вигляду називають силогізмами. Форма міркування вважається правильною, якщо при істинності вихідних тверджень, вона завжди приводить до правильних висновків. Цілком зрозуміло, що при хибності вихідних тверджень навіть за допомогою правильного за формою міркування, можна прийти до хибного висновку.
Якщо проаналізувати наведені приклади з точки зору їх істинності, то одержимо таке: 1) у першому прикладі з двох правильних висловлень ми одержуємо істинний висновок; 2) хибність висновку другого прикладу відбулася не від хибності схеми, а від хибності однієї з посилок; 3) у третьому прикладі, незважаючи на істинність всіх висловлень, ми одержуємо логічну помилку у висновку; 4) четвертий приклад є ілюстрацією до третього. Таким чином, логічні висновки повинні робитися за певною схемою, а правильними вважаються лише ті схеми, які з істинних посилок завжди приводять до істинних висновків.
В аристотелівській логіці розглядаються чотири види так званих категоричних судження: 1) загально стверджувальне судження – А=«Всі S суть P»; 2) загальнозаперечувальне судження – Е=«Всяке S не є P»; 3) частково стверджувальне судження – І=«Деякі S суть P»; 4) частковозаперечувальне судження – О=«Деякі S не суть P». Їх прийнято класифікувати, по-перше, «по якості»: А, І – стверджувальні судження; Е, О – заперечувальні судження; по-друге, «по кількості»: А, Е – загальні судження; І, О – часткові судження. Розглянемо всі чотири види суджень з точки зору теорії предикатів.
Для запису загально стверджувального судження А=«Всі S суть P» використаємо квантор загальності, предикати S(х) і P(х) та імплікацію предикатів S(х)→P(х). Тоді символічний запис цього судження буде мати вигляд ("хєХ)(S(х)→P(х)) та читатиметься так: «для всіх хєХ, якщо х має властивість S, то х має властивість Р». Прикладом таких тверджень є «всі риби - тварини», «всі люди - смертні», «всі квадрати – прямокутники» тощо.

 Для запису загальнозаперечувальне судження Е=«Всяке S не є P» використаємо квантор загальності, предикат S(х), заперечення предикату P(х) та імплікацію предикатів S(х)→P(х). Тоді символічний запис цього судження буде мати вигляд ("хєХ)(S(х)→P(х)) та читатиметься так: «для всіх хєХ, якщо х має властивість S, то х немає властивості Р». Прикладом таких тверджень є «всі риби не є птахами», «будь-які камені не є тваринами», «будь-які трикутники не є квадратами» тощо.
Для запису загальнозаперечувальне судження Е=«Всяке S не є P» використаємо квантор загальності, предикат S(х), заперечення предикату P(х) та імплікацію предикатів S(х)→P(х). Тоді символічний запис цього судження буде мати вигляд ("хєХ)(S(х)→P(х)) та читатиметься так: «для всіх хєХ, якщо х має властивість S, то х немає властивості Р». Прикладом таких тверджень є «всі риби не є птахами», «будь-які камені не є тваринами», «будь-які трикутники не є квадратами» тощо.
Для запису частково стверджувального судження І=«Деякі S суть P» використаємо квантор існування, предикати S(х) і P(х) та кон’юнкцію предикатів S(х)ÙP(х). Тоді символічний запис цього судження буде мати вигляд ($хєХ)(S(х)ÙP(х)) та читатиметься так: «існує таке хєХ, який має властивість S і також має властивість Р». Прикладом таких тверджень є «деякі люди палять», «деякі швейцарці говорять французькою», «деякі прості числа - парні» тощо.

 Для запису частковозаперечувального судження О=«Деякі S не суть P» використаємо квантор існування, предикат S(х), заперечення предикату P(х) та кон’юнкцію предикатів S(х)ÚP(х). Тоді символічний запис цього судження буде мати вигляд ($хєХ)(S(х)ÚP(х)) та читатиметься так: «існує таке хєХ, який має властивість S і також немає властивості Р». Прикладом таких тверджень є «деякі тварини не дихають легенями», «деякі гриби не їстівні», «деякі трикутники не рівнобедрені» тощо.
Для запису частковозаперечувального судження О=«Деякі S не суть P» використаємо квантор існування, предикат S(х), заперечення предикату P(х) та кон’юнкцію предикатів S(х)ÚP(х). Тоді символічний запис цього судження буде мати вигляд ($хєХ)(S(х)ÚP(х)) та читатиметься так: «існує таке хєХ, який має властивість S і також немає властивості Р». Прикладом таких тверджень є «деякі тварини не дихають легенями», «деякі гриби не їстівні», «деякі трикутники не рівнобедрені» тощо.
На основі наведених суджень можна легко побачити деякі співвідношення між ними, які детально вивчалися в аристотелівській логіці. Наприклад, загальностверджувальне судження А і частковозаперечувальне судження О є запереченнями один одного. Аналогічно загальнозаперечувальне судження Е і частково стверджувальне судження І є запереченнями один одного. У традиційній логіці говорять, що загальностверджувальне судження А і частковозаперечувальне судження О (загальнозаперечувальне судження Е і частковостверджувальне судження І) знаходяться у відношенні протиріччя один до одного. Таким чином, аристотелівські силогізми являють собою схеми логічних виводів, які складаються з трьох суджень одного з названих чотирьох видів А, Е, І, О. Наведемо приклади силогізмів, які є досить поширеними (див. таблицю №14).
| Силогізм Barbara | Силогізм Darii | |
| «Всі М суть Р» «Всі S суть М» «Всі S суть Р» | «Всі М суть Р» «Деякі S суть М» «Деякі S суть Р» | «Деякі М суть Р» «Деякі S суть М» «Деякі S суть Р» |
| Риска після другого висловлення означає, що висновок є логічним наслідком посилок. | Риска після другого висловлення означає, що висновок є логічним наслідком посилок. | Риска після другого висловлення означає, що висновок є логічним наслідком посилок. |
| Всі висловлення цього силогізму є загальностверджувальними. | У даній схемі перша посилка є загальностверджувальним висловленням, а друга посилка і наслідок – частковостверджувальні. | У даній схемі всі три судження є частковостверджувальними. |
Таблиця № 14. Приклади силогізмів.
Вважають, що в основі кожного дедуктивного міркування лежить певне правило виводу, серед яких ми виділимо такі:
1. Правило заключення, яке символічно запишеться так: ("хєХ)(А(х)®В(х)ÙА(a))®В(a). У цьому записі вираз ("хєХ)(А(х)®В(х)ÙА(a)) являє собою умову (посилку) міркування, яка представлена кон’юнкцією загальної та часткової посилки. У свою чергу вираз В(a) - це заключення або висновок міркування. Крім цього, А(a) - це часткова посилка, яка являє собою висловлення, одержане із предиката А(х) після підстановки замість змінної х конкретного значення, а В(a) – це висловлення, одержане із предиката В(х) після підстановки замість змінної х конкретного значення.
2. Правило заперечення, яке символічно запишеться так: ("хєХ)(А(х)®В(х)ÙВ(a))®А(a). У цьому записі вираз ("хєХ)(А(х)®В(х)ÙВ(a)) являє собою умову (посилку) міркування, яка представлена кон’юнкцією загальної та часткової посилки. У свою чергу вираз В(a) - це часткова посилка, яка являє собою висловлення, одержане із предиката В(х) після підстановки замість змінної х конкретного значення, а А(a) – це заключення або висновок міркування. Крім цього, А(a) - це висловлення, одержане із предиката А(х) після підстановки замість змінної х конкретного значення.
3. Правило силогізму, яке символічно записується так: ("хєХ)((А(х)→В(х)ÙВ(х)→С(х))→(А(х)→С(х))). Це правило виводу складається із двох загальних посилок ("хєХ)((А(х)→В(х))Ù(В(х)→С(х))), кон’юнкція яких задає нам умову міркування. Імплікація А(х)→С(х) є загальним висновком міркування.
Якщо множини істинності предикатів А(х), В(х) і С(х) зображати кругами Ейлера, то правильність міркувань можна перевірити за допомогою діаграм Ейлера-Венна. Для представлених у таблиці № 15 силогізмів будемо мати такі діаграми Ейлера-Венна (див. діаграми №№ 3-5).

Діаграма № 3: перевірка правильності силогізму Barbara за допомогою кругів Ейлера.

Діаграма № 4: перевірка правильності силогізму Darii за допомогою кругів Ейлера.

Діаграма № 5: перевірка правильності силогізму, який містить частково стверджувальні судження за допомогою кругів Ейлера.
Вправа: перевірити правильність міркування ((А(х)→В(х))Ù(В(х)→С(х)))→(А(х)→С(х)), використовуючи круги Ейлера, якщо А(х): “натуральне число х кратне 16”, В(х): “натуральне число х кратне 8”, С(х): “натуральне число х кратне 4”.
Розв’язання:
Позначимо через А множину чисел, кратних 16, через В – множину чисел, кратних 8, і через С множину чисел, кратних 4. Тоді відношення між цими множинами за допомогою кругів Ейлера зобразиться так (див. діаграму № 6).
Із наведеної діаграми видно: із того, що число х кратне 16 випливає, що число х кратне 8, а із того, що число х кратне 8 випливає, що воно кратне 4. Таким чином, використовуючи правило силогізму, ми також можемо переконатися у правильності вказаного міркування.

Діаграма № 6: перевірка правильності міркувань за допомогою кругів Ейлера.
5*. Алгоритми. Основні властивості алгоритмів. Приклади алгоритмів, що використовуються в курсі математики початкової школи.
5*. Поняття алгоритму зустрічається як в математиці, так і в повсякденному житті. Точне визначення алгоритму в математиці не в усьому співпадає з інтуїтивним розумінням цього поняття в практичній діяльності людей. Термін алгоритм увійшов у активний словниковий запас людей завдяки значному застосуванню електронно–обчислювальної техніки в сучасному виробництві. Поняття алгоритму є одним із основних понять математики та інформатики. Ще задовго до використання інформатики в математиці застосовувалися різні алгоритми (або алгорифми). Зокрема, алгоритм письмового додавання, віднімання, множення, ділення, розкладу числа на прості множники, алгоритм Евкліда для знаходження НСД тощо.
Під алгоритмом розуміють точні вказівки щодо виконання у певному порядку деякої серії операцій для розв’язування задач певного типу. Наприклад: для рівняння ах=b маємо: 1. Якщо а≠0, то х=b:а. 2. Якщо а=0 і b≠0, то рівняння розв’язку немає. 3. Якщо а=b=0, то рівняння 0х=0 має безліч розв’язків, тобто х - будь-яке дійсне число.
Застосування алгоритму через скінченне число кроків приводить до розв’язання кожної задачі даного типу. Спільним для всіх алгоритмів є його характерні ознаки, до яких відносимо:
- повну визначеність алгоритму, тобто алгоритм повинен привести до результату;
Дата добавления: 2015-11-04; просмотров: 1172;
