Перестановки з повтореннями та без повторення.

4. Комбiнацiї та їх властивості.

Література:

[1] – с. 41-51; [2] – с. 54-64; [3] – с. 56-79.

1. Комбiнаторнi задачі. Правила суми i добутку.

1. Розглядаючи множини та операції над ними ми вказували, що порядок розміщення елементів немає значення, але є галузь математики, для якої порядок розміщення елементів множини має суттєве значення. Ця галузь математики називається комбінаторикою та розглядає задачі, пов’язані з розташуванням за певними правилами елементів скінченних множин i відшукання числа способів, якими це можна зробити. Такі задачі називаються комбінаторними. Наприклад: 1) скільки карточок спортлото потрібно купити, щоб точно вгадати 6 номерів? 2) скількома способами можна призначити в групі трьох чергових?; 3) скількома способами можна витягнути з колоди три карти, щоб набрати 21 очко?

Комбінаторика виникла з необхідності створення теорії азартних ігор. Найбільший вклад в її розвиток внесли П.Ферма, Б.Паскаль, Х.Гюйгенс, В.Лейбнiц, Я.Бернуллi. Значний інтерес до комбінаторики поновлюється в 50-х роках XX ст. у зв’язку з бурхливим розвитком кібернетики та дискретної математики i широким використанням електронно-обчислювальної техніки. Дуже широко використовується комбінаторика в теорії оптимального управління.

В комбінаториці є правила, які дозволяють елементарними способами розв’язати значну кількість комбінаторних задач. Розглянемо дві скінченні множини А i В такі, що n(A)=m і n(B)=k, причому АÇB=Ø. Якщо виконуються ці умови, то кількість елементів множини АÈВ визначається однозначно, тобто n(АÈВ)=m+k. Отже має місце таке твердження:

Правило суми: якщо множина А містить m елементів, а множина В - k елементів то множина AÈB містить m+k елементів.

Досить часто правило суми формулюють так:

Правило суми: якщо деякий елемент x з множини А можна вибрати m способами, а елемент y з множини В - k способами, причому жоден із способів вибору елемента x не співпадає зі способом вибору елемента y, то елемент x або елемент y можна вибрати m + k способами.

Це правило можна поширити на випадок будь-якої скінченної кількості множин. Розглянемо застосування цього правила до розв’язання наступних задач.

Задача 1: на столі є 4 ручки i 3 олівці. Скількома способами можна взяти зі столу один предмет?

Розв’язання:

У цій задачі маємо справу із двома скінченними множинами: А - множина ручок, де n(A)=4, i В - множина олівців, де n(B)=3. Оскільки нам потрібно вибрати один предмет, тобто зробити вибір x чи y (ручка або олівець), то згідно з правилом суми це можна зробити n(A)+n(B)=4+3=7 способами. Правило суми можна було застосувати тому, що множини не перетинаються i вибір ручки не залежить від вибору олівця i навпаки.

Задача 2: із 28 студентів групи: 15 - займається в секції волейболу, 12 – в секції футболу, 7 - займається в обох секціях. Скільки студентів займається в інших секціях.

Розв’язання:

У цій задачі мова йде про такі множини: А - множина студентів групи, де n(A)=28, В - множина студентів, які займаються волейболом, де n(B)=15, С - множина студентів, які займаються футболом, де n(C)=12, D - множина студентів, які займаються футболом i волейболом, де n(D=ВÇС)=7, K - множина студентів, які займаються в інших секціях, де n(K) потрібно знайти. На кругах Ейлера ці множини зобразяться так (див. малюнок № 21):

Малюнок № 21. Розв’язання задачі 2.

Отже, n(A)=n(B)+n(C)+n(K)-n(BÇC), 28=15+12+n(K)-7, n(K)=8 - кількість студентів, які займаються в інших секціях.

Інше правило комбінаторики відноситься до підрахунку числа кортежів, які можна утворити із елементів даних скінченних множин. Розглянемо дві скінченні множини А і В такі, що n(A)=m і n(B)=k. Утворимо множину А×В та знайдемо число її елементів, тобто n(А×В). Розглядаючи декартів добуток множин, ми з’ясували, що n(А×В)=n(А)•n(В)=m•k. Таким чином, можна сформулювати наступне правило.

Правило добутку: якщо елемент x із множини А можна вибрати m способами, а елемент y із множини B - k способами, то пару (x,y)єА×В можна вибрати m•k способами.

Символічно це правило можна записати так: n(А×В)=n(А)•n(В)=m•k. Його можна поширити на випадок будь-якої скінченної кількості множин. Покажемо застосування правила добутку на наступній задачі.

Задача: скільки трицифрових чисел можна записати, використовуючи цифри 1,2,3,4,5?

Розв’язання:

У цій задачі мова йде про п’ятиелементну множину А={1,2,3,4,5}, із елементів якої треба вибрати трьохелементні підмножини. Кожне трицифрове число являє собою впорядковану трійку цифр або впорядкований кортеж довжини три, наприклад: 111, 112, 121 тощо. Отже, для того, щоб скористатися правилом добутку, потрібно розглянути декартовий добуток трьох множин А×А×А. Оскільки, згідно з правилом добутку n(A×A×A)=n(A)×n(A)×n(A), то число трицифрових чисел, які можна скласти із цифр 1, 2, 3, 4, 5 дорівнює 125. Отже, із цифр 1, 2, 3, 4, 5 можна утворити 125 трицифрових чисел.

2. Розміщення з повтореннями та без повторень.

2.В останній задачі попереднього пункту ми утворювали впорядковані кортежі довжини три із елементів скінченної п’ятиелементної множини, причому деякі елементи повторювались 2 або 3 рази. Наприклад 112 i 111. В комбінаториці такі кортежі називають розміщеннями з повтореннями із заданих n елементів по k елементів. Число розміщень з повтореннями позначається так: Ã_n^k. Цей символічний запис читають: число розміщень з повтореннями із n елементів по k. Для визначення числа розміщень з повтореннями приймемо наступні означення та доведемо теорему.

Означення: розміщеннями з повтореннями із елементів n - елементної множини Х по k елементів називають кортежі довжини k, утворені із елементів цієї множини Х i компоненти яких повторюються.

Теорема 1: число розміщень з повтореннями із даних n елементів по k елементів обчислюється за формулою Ã_n^k=n^k.

Доведення:

Розглянемо скінченну множину Х таку, що n(Х)=n. Щоб утворити кортеж довжини k із елементів цієї множини Х, потрібно розглянути декартовий добуток множини Х саму на себе Х×Х×Х×...×Х, який містить k

k

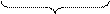елементів, бо кожен кортеж довжини k є елементом декартового добутку. Згідно з правилом добутку число елементів цієї множини Х×Х×Х×...×Х

k

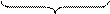
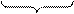дорівнює n(Х×Х×Х×...×Х)=n(Х)×n(Х)×n(Х)×...×n(Х)=n•n•n•...•n=nk. Теорему

k k k

доведено.

Застосування доведеної теореми проілюструємо на прикладі наступної задачі, подібну до якої ми раніше розв’язали, використовуючи правило добутку.

Задача: скільки п’ятицифрових чисел можна утворити із цифр 1, 2, 3, 4, 5?

Розв’язання.

Оскільки в задачі нічого не говориться про те повторюються чи не повторюються цифри в записі чисел, то будемо вважати, що вони повторюються. Отже, в задачі є п’ятиелементна множина Х={1,2,3,4,5}, де n(Х)=5. Із елементів цієї множини потрібно утворювати впорядковані кортежі довжиною 5, бо нам потрібні п’ятицифрові числа, а, оскільки, цифри можуть повторюватися, то мова йде про розміщення з повтореннями. Отже, будемо використовувати формулу для обчислення числа розміщень з повтореннями, тобто Ã_n^k=n^k. У нашому випадку n(Х)=5, k=5, а тому Ã₅⁵=5⁵=3125. Таким чином, число розміщень з повтореннями із 5 елементів по 5 елементів дорівнює 3125.

У комбінаториці крім розміщень з повтореннями розглядаються розміщення без повторень. Для того, щоб навчитися їх обчислювати введемо означення та доведемо відповідну теорему.

Означення: розміщенням із даних n елементів скінченної множини Х по k елементів називаються впорядковані кортежі довжини k, утворені із елементів множини Х, компоненти яких не повторюються.

Число розміщень без повторень символічно позначається А_n^k i читається: число розміщень із даних n елементів по k елементів або А із n по k.

Теорема: Число розміщень з n елементів по k дорівнює добутку k послідовних натуральних чисел із яких найбільшим є n.

Символічно сформульована теорема запишеться так: А_n^k=n(n-1)(n-2)...(n-k+1)=n!/(n-k)!

Доведення.

Розглянемо скінченну множину Х таку, що n(Х)=n. Будемо утворювати із елементів цієї множини кортежі довжиною k, де k≤n. Оскільки в множині Х є n елементів, то перший компонент кортежу можна вибрати n способами, другий – n-1 способом, третій - n-2 способами, і нарешті k-й – n-(k-1)=n-k+1 – способом. Згідно правила добутку число А_n^k таких кортежів довжини k буде дорівнювати n(n-1)(n-2)...(n-k+1). Отже, А_n^k=n(n-1)(n-2)...(n-k+1). Теорему доведено.

У математиці добуток всіх послідовних чисел від 1 до деякого числа k прийнято позначати спеціальним символом k! та називати k-факторіал. Наприклад: 3!=1•2•3=6; 5!=1•2•3•4•5=120; 7!=1•2•3•4•5•6•7=5040; k!=1•2•3•...•k. У математиці прийнято вважати, що 0!=1 i 1!=1. Використовуючи ці позначення, спробуємо перетворити формулу для знаходження числа розміщень. У формулі А_n^k є добуток всіх натуральних чисел від n до n-k+1, але немає добутку від 1 до n-k. Щоб одержати цей добуток i не змінити значення формули, домножимо й поділимо вираз у правій частині формули на добуток послідовних натуральних чисел від 1 до n-k. А_n^k=(n•(n-1)•(n-2)•...•(n-k+1)(n-k)•(n-k-1)•…3•2•1)/((n-k)•(n-k-1)•…3•2•1)= n!/(n-k)!. Це зроблено тому, що в чисельнику є добуток всіх послідовних чисел від 1 до n. Отже, чисельник можна записати як n!. У знаменнику є добуток всіх послідовних натуральних чисел від 1 до n-k, то запишемо його з використанням факторіалу, тобто (n-k)!.

Покажемо застосування виведених формул для обчислення числа розміщень на прикладі наступної задачі.

Задача: скільки двозначних чисел можна записати за допомогою цифр 2, 4, 5, 6, 7 так, щоб цифри не повторювалися?

Розв’язання.

У задачі йдеться про п’ятиелементну множину {2, 4, 5, 6, 7}, із якої слід вибирати кортежі довжини два так, щоб елементи, тобто цифри, не повторювалися. Отже, необхідно обчислити число розміщень без повторень із п’яти елементів по два елемента. Використаємо формулу А_n^k=n(n-1)(n-2)...(n-k+1), в якій n=5, k=2. Обчислюємо А₅²;=5•(5-1)=5•4=20. Таким чином, за допомогою цифр 2, 4, 5, 6, 7 можна записати 20 двозначних чисел так, щоб вони не повторювалися.