Последовательные алгоритмы структурного синтеза

Алгоритмы такого вида относятся к классу эвристических. Их достоинством является высокая экономичность по затратам машинного времени и требуемому объему оперативной памяти за счет отсутствия процедуры многоразового анализа вариантов структуры. Однако последовательные алгоритмы дают не оптимальные, а близкие к оптимальным решения.

Рассмотрим задачу компоновки (монтажной платы), т. е. определения состава типовых конструкций каждого уровня. Задача компоновки решается «снизу вверх», т. е. известные схемы (i - 1)-го уровня необходимо распределить по конструкциям i-го уровня. Например, на самом низшем уровне элементами могут быть корпуса микросхем, а конструкциями (блоками) — типовые элементы замены, связанные друг с другом путем разъемных соединений.

В качестве критериев оптимальности при решении задач компоновки используют критерии либо минимума суммарного числа 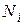типов модулей

,

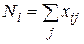где 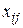— число модулей j-го типа i-го уровня схемы, либо минимума межблочных соединений

,

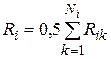где 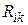— число внешних связей каждого модуля i-го уровня.

Первый критерий связан с конструктивными характеристиками аппаратуры и показателем технологической стоимости, второй критерий ведет к повышению надежности конструктивной реализации схемы за счет сокращения числа разъемных соединений, уменьшению помех и задержек сигналов благодаря снижению числа межблочных соединений [44].

3.4. Алгоритм компоновки по критерию минимума межблочной связности

Первоначально выбирают исходный элемент схемы. Выбор начального элемента основывается на схемотехнических соображениях:

1) В первый компонуемый узел включены все элементы, смежные с начальным, и сам начальный элемент.

2) Если полученное число элементов равно максимально допустимому числу элементов в первом узле, то компоновка узла заканчивается.

3) Если это число больше или меньше максимально допустимого, то выполняются операции по устранению лишних или добавлению недостающих элементов, причем из нескомпонованных элементов выбирают такой, который имеет наибольшее число связей с элементами, уже вошедшими в состав компонуемого узла.

4) Далее сформированный узел удаляют из схемы и компонуют новые узлы.

5) Процесс повторяется до тех пор, пока схема не будет разбита на требуемое число частей или не будет выяснена невозможность этого.

Сформулируем описанный алгоритм в терминах теории графов. Пусть задан граф схемы G = (X, U), который необходимо разбить на l частей 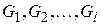с числом вершин в каждом соответственно .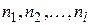

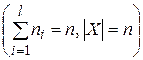Первоначально в графе G определяют вершину 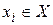с наибольшей локальной степенью 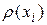(локальной степенью 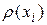вершины 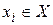называют число ребер, инцидентных этой вершине графа). Если таких вершин несколько, то предпочтение отдается той, которая имеет большее число кратных ребер. Вершина x, и все смежные с ней вершины включаются в граф G₁. Обозначим это множество вершин через 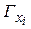. Если 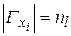, то G₁ образован, если же 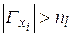, то из графа G₁ удаляют вершины, связанные с остающимися вершинами графа G меньшим числом ребер. Когда 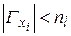, выбирают вершину 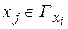, удовлетворяющую условиям

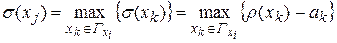
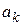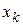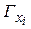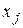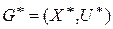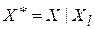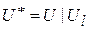где — число ребер, соединяющих вершину со всеми невыбранными вершинами графа G. Строят множество вершин , смежных , и процесс выбора вершин G₁ повторяют. Образованный подграф G₁ исключают из исходного и получают граф , где , . Далее в графе 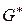выбирают вершину с наибольшей локальной степенью, включают ее в G₂ и процесс повторяют до тех пор, пока граф G не будет разрезан на l частей.

Первоначальную компоновку можно улучшить с помощью итерационных алгоритмов, основанных на реализации методов парных или групповых перестановок элементов из одной части схемы в другую таким образом, чтобы улучшилось значение целевой функции с учетом заданных ограничений.

Задача размещения

Эта задача заключается в оптимальном размещении (с точки зрения выбранного критерия оптимальности) элементов и связей между ними в монтажном пространстве типовой конструкции с учетом заданных конструктивно-технологических ограничений [9].

Исходными данными в задаче являются принципиальная электрическая схема узла или устройства, метрические параметры и топологические свойства монтажного пространства. Главная цель размещения — создание наилучших условий для трассировки с учетом обеспечения тепловых режимов и электромагнитной совместимости электрорадиоэлементов. Несмотря на обилие существующих критериев размещения (минимума пересечений, минимума суммарной длины соединений и т. д.), истинной целью размещения компонентов является максимальное упрощение процесса трассировки соединений, т. е. достижение минимального числа непроведенных трасс [5—7]. При размещении п микроэлементов в регулярном монтажном пространстве с числом позиций т общее число размещений N(n, т) определяется как

.

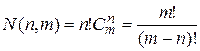В связи с этим поиск оптимального размещения с помощью перебора нецелесообразен уже при n >15.

Имеется много разновидностей алгоритмов размещения. Основной идеей этих алгоритмов является идея упорядочения микроэлементов по определенным признакам. Во-первых, сначала устанавливают очередность микроэлементов, а затем для каждого из них определяют наилучшую позицию по выбранному критерию, например по суммарной длине связей с уже размещенными компонентами. Во-вторых, затем процесс повторяют для оставшихся компонентов и свободных позиций. Связность размещаемых элементов задается матрицей смежности R графа G = (X, U). Для выбора размещаемого элемента используют различные оценки связности.

Пусть на k-м шаге алгоритма размещено 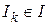элементов, тогда 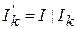— множество еще не размещенных элементов. Основными правилами для выбора элементов на (k+1)-м шаге алгоритма являются:

а) максимум суммарной связности 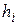со всеми размещенными элементами:

;

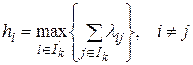б) максимум разности связей/ между размещенными и не размещенными элементами:

.

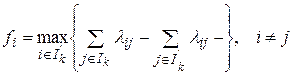Выбранный для размещения элемент устанавливают в такую позицию среди оставшихся незаполненных, при которой будет иметь наименьшее значение некоторая целевая функция.

Для многих задач размещения в качестве такой функции может быть выбрана суммарная длина связей с уже размещенными элементами [7,8].

Последовательные алгоритмы размещения требуют небольших затрат машинного времени, относят их к классу полиномиальных алгоритмов со сложностью О(п), приводящих к неоптимальным решениям. Улучшить решение можно применением итерационных алгоритмов компоновки, основанных на изменении позиций одиночных элементов или групп элементов. Итерационные алгоритмы также относятся к классу полиномиальных со сложностью порядка О(п²)-О(п⁴).

Задача трассировки

Данная задача заключается в определении конкретной геометрии печатного или проводного монтажа, реализующего соединения между элементами схемы. Исходными данными для трассировки являются список цепей, метрические параметры и топологические свойства типовой конструкции и ее элементов, а также результаты решения задачи размещения, по которым находят координаты выводов элементов.

При решении задачи трассировки строят множество трасс, соединяющих выводы элементов соответствующих цепей схемы. Разработка отдельной трассы представляет собой построение на фиксированных вершинах минимального покрывающего или связывающего «дерева», а разработка множества трасс сводится к построению «леса» непересекающихся минимально покрывающих или связывающих «деревьев». Известно, что на п вершинах можно построить 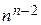различных «деревьев», поэтому точное решение задачи трассировки методом полного перебора практически нереализуемо.

В последовательных алгоритмах трассировки трассы цепей проводятся в определенном порядке одна за другой, при этом каждая проложенная трасса становится препятствием для всех последующих цепей. В последовательных алгоритмах выполняют локальную оптимизацию качества трассировки каждой отдельной трассы без учета влияния размещения данной трассы на возможность проведения последующих. Это приводит к тому, что некоторые участки платы могут оказаться заблокированными.

Известный алгоритм трассировки основан на волновом методе (алгоритм Ли). Главные принципы волнового алгоритма Ли заключаются в следующем. Плоскость трассировки разбивают на прямоугольные площадки — дискреты заданного размера. Размер дискретной площадки определяется допустимыми размерами проводников и расстояниями между ними. Задача проведения трасс сводится к получению последовательности дискретов, соединяющих элементы а и b, соответствующие началу и концу проводимой трассы.

Введем целевую функцию 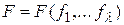как критерий качества пути.

Начиная с элемента, а дискретам, соседним с ранее просмотренными, присваивают определенное значение целевой функции 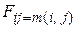. Этот этап проводится итерационно до элемента b, которому присваивают некоторое значение веса 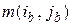. Затем, начиная от элемента b, значения перемещаются к элементу, а по пройденным дискретам таким образом, чтобы значения целевых функций дискретов монотонно убывали. В результате получается трасса, соединяющая элементы а и b.

Обычно работа алгоритма Ли реализуется следующим образом. На трассируемой плоскости из источника а моделируется распространение волны до тех пор, пока не будет достигнута точка b или пока на некотором шаге фронт волны не сможет включить ни одного незанятого дискрета. Эту часть алгоритма называют распространением волны.

После этого проводят трассу, начиная от конечной точки b, по дискретам с последовательно уменьшающимися весами (рис. 3.16). Цифры в квадратах соответствуют весам дискретов, занятые дискреты заштрихованы, а построенная трасса показана штриховой линией. Существует несколько вариантов проведения пути, из которых конструктор (или ЭВМ) выбирает один, наиболее удовлетворяющий заданным требованиям.

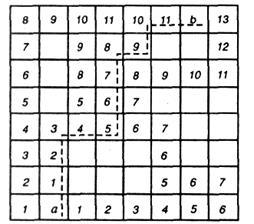
Рис. 3.16 – Трассируемая плоскость

Имеется многообразие волновых алгоритмов, направленных на повышение быстродействия трассировки, уменьшение объема требуемой оперативной памяти ЭВМ и т. д. Волновые алгоритмы применяются при разработке сетей ЭВМ [15, 16].