Алгоритмы (свойства, реализация алгоритмов)
Алгоритм решения задачи – это система точных и понятных предписаний о содержании и последовательности выполнении конечного числа действий, необходимых для решения любой задачи данного типа.
Алгоритм – это конечный набор правил, последовательное применение которых к обрабатываемой информации за конечное число шагов позволяет получить результаты обработки (правила выполнения арифметических действий, правила решения определенных видов уравнений и т.д.).
Слово алгоритм появилось в результате искажения (после перевода на европейские языки) имени выдающего математика IX века Аль –Хорезми, которым были описаны правила выполнения основных арифметических действий в десятичной системе счисления. Понятие алгоритма возникло и используется ранее, чем появление ЭВМ.
Основные свойства алгоритма:
1. Дискретность, т.е. пошаговый характер определяемого им процесса. Описываемый процесс должен быть разбит на последовательность отдельных шагов. При каждом шаге работы алгоритма известно, что считать результатом шага.
2. Детерминированность (однозначность или определенность). Процесс применения правил к исходным данным определен вполне однозначно, результат работы алгоритма также будет однозначен. Запись алгоритма должна быть настолько четкой, полной, продуманной в деталях, чтобы у исполнителя не могло возникать потребности в принятии каких-либо самостоятельных решений, не предусмотренных составителем алгоритма.
3. Массовость. Необходимы алгоритмы, обеспечивающие решение широкого класса задач данного типа. Они предполагают возможность использовать различные допустимые значения исходящих данных.
Например: решение уравнения ах2+вх+с=0 в области действительных чисел может быть найдено по формуле:
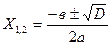 , которые применяемы не для одного, а для многих квадратных уравнений с коэффициентами а, в, с, удовлетворяющих условию
, которые применяемы не для одного, а для многих квадратных уравнений с коэффициентами а, в, с, удовлетворяющих условию
D=в2 -4ас 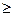 0
0
4. Результативность. При точном исполнении всех предписаний алгоритма процесс должен прекратиться за конечное число шагов и при этом должен быть получен какой-либо определенный ответ на вопрос задачи.
Под алгоритмизацией понимают процесс разработки алгоритма решения какой-либо задачи.
Формы (способы) записи алгоритмов:
1) Словесный способ алгоритма – содержание последовательных шагов вычислений задается в произвольной форме на естественном языке. Например:
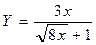
1. Прочитать заданное значение х.
2. Умножить х на 8.
3. Из результата второго действия (шага) извлечь квадратный корень.
4. К результату третьего действия прибавить 1.
5. Умножить х на 3.
6. Результат пятого действия разделить на результат четвертого действия.
7. Записать значение результата у.
Недостатки: низкая наглядность и слабая формализация. Этим способом можно описывать алгоритмы с произвольной степенью детализации.
2) Формульно-словесный способ основывается на задании последовательных шагов алгоритма с помощью математических формул и выражений в сочетании со словесными выражениями. Например:
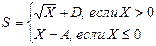
1. Если Х>0, то перейти к шагу 2, в противном случае перейти к шагу 3.
2. Положить S= 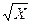 +D. Перейти к шагу 4.
+D. Перейти к шагу 4.
3. Положить S=X-A. Перейти к шагу 4.
4. Принять S за искомый результат и остановиться.
Он более компактен и нагляден, но не является строго формальным.
3) Операторные схемы записи алгоритмов – это аналитическая форма представления алгоритма с помощью операторов, описывающих содержание отдельных участков вычислительного процесса. Участки алгоритма могут разделяться по своему назначению. Одни участки предусматривают вычисления с помощью арифметических операций, другие предназначены для проверки некоторых условий, выполнение которых определяет порядок работы алгоритма. Первые называются арифметическими операторами, вторые – логическими операторами. Имеется также группа специальных операторов управления (ввод-вывод данных, оператор останова и т.д.). Весь процесс решения задач состоит из последовательности выполнения таких операторов. Обозначения операторов:
B- ввод исходных данных
A- арифметический оператор
П - оператор печати (вывода)
Р - логический оператор
Я - оператор останова
Операторы имеют номера-индексы в соответствии с порядком их исследования. Логический оператор записывается как функция, аргументом которой служит проверяемое условие P (i=N) или P(υ ≤o)и т.д.
Операторы выполняются последовательно, которые могут нарушить логические операторы и безусловные операторы передачи управления. Если окажется, что проверяемое условие истинно, то очередным становится оператор, стоящий справа от логического оператора, в противном случае, когда логическое условие не соблюдается, оператор – приемник указывается стрелкой. Отсутствие передачи управления от оператора слева к соседнему оператору справа обозначается точкой с запятой (;). Алгоритм завершается оператором останова.
Операторная схема алгоритма сопровождается схемой счета.
Например:
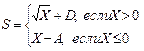
Схема счета представлена в виде таблицы
| № | Символ-оператор | Содержание оператора |
| В1 Р2 А3 А4 П5 Я6 | Ввод исходных данных
Проверка выполнения логического условия (X>0)
Вычисление значения 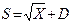 Вычисление значения S= X-A
Печать вычисленного значения S
Останов
Вычисление значения S= X-A
Печать вычисленного значения S
Останов
| |
Операторная схема выглядит следующим образом:
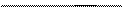 B1 P2 (х>0) А3; А4 П5 Я6 B1 P2 (х>0) А3; А4 П5 Я6
|
Ввел этот метод А.А. Ляпунов в 1954 году. Операторные схемы имеют формальный уровень, близкий к алгоритмическим языкам, и поэтому могут рассматриваться как средство автоматизации программирования.
4) Метод блок-схемы – это графическое изображение логической структуры алгоритма. На блок-схеме каждый этап процесса обработки представляется в виде геометрических фигур (блоков), имеющих определенную конфигурацию в зависимости от характера вычисляемых операций.
Блок может иметь имя (метку). Линия соединения блоков показывает направление процесса обработки данных. Каждое направление называется ветвью.
Перечень блоков, их наименование, функции, формы, размеры определяются ГОСТ 19.003—80. Указанный ГОСТ регламентирует изображение и размеры отдельных блоков в блок-схеме, а также их взаимное расположение. Основные виды блоков приведены в табл. 5.2.
Таблица 5.2
Блок-схемы алгоритмов
| Наименование блока | Графическое представление блока | Функция блока |
| Линейный процесс | 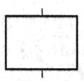
| Выполнение операции или группы операций, в результате которых изменяются значение, форма представления или расположение данных |
| Проверка условия, логическое решение | 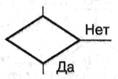
| Выбор направления выполнения алгоритма в зависимости от некоторых переменных условий |
| Ввод-вывод | 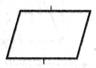
| Преобразование данных в форму, пригодную для обработки (ввод) или отображения результатов обработки (вывод) |
| Начало-конец алгоритма (пуск-остановка) | 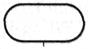
| Начало, конец процесса обработки данных |
| Предопределенный (заранее описанный) процесс, модуль | 
| Использование ранее созданных или отдельно описанных алгоритмов (модулей) |
| Соединитель | 
| Указание связи между прерванными линиями потока обработки данных |
Например:
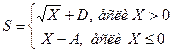
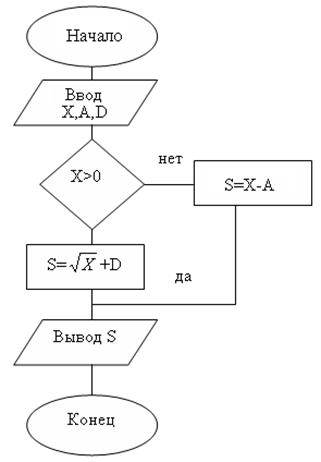
5) Псевдокод или структурно-стилизованный способ записи алгоритма основан на формализованном представлении предписаний. Разновидность: алгоритмический язык в русской нотации. Это например:
алг. запись
арг. истина
если ложь
нач. массив
кон.
Важнейшая особенность – близость к алгоязыкам программирования.
6) Язык программирования используется для записи алгоритмов в виде, непосредственно доступном ЭВМ.
Программа, написанная на языке программирования, представляет собой последовательность операторов, реализующих заданный алгоритм.
Языки программирования высокого уровня: ФОРТРАН, БЕЙСИК, КОБОЛ, АЛГОЛ, ПАСКАЛЬ, СИ, ПЛ/1 и др.
Например:
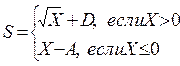
На языке Бейсик это выглядит следующим образом:
10 INPUT «Исх. данные», Х, D, А
20 IF X>0 THEN 5 Ø
30 S=Х- А
40 Goto 6 Ø
50 S=SQR (X) +D
60 PRINT «Результат=», S
70 END
Дата добавления: 2015-09-18; просмотров: 2658;
