Представление схемы гиперграфом и ультраграфом

Рассмотрим модель в виде гиперграфа, когда множество элементов схемы Э соответствует множеству X, а множество электрических цепей С — множеству ребер U (|X| = n — число элементов в схеме; |U| = m — число электрических цепей схемы). Каждое ребро гиперграфа 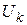представляется подмножеством тех вершин 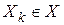которым соответствуют элементы, соединенные k-й электрической цепью.

При задании схемы гиперграфом учитывается фактор неизвестности соединения, т. е. для определения связи между i-м и j-м элементами схемы
k-электрической цепью, достаточно проверить условие 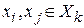. Так как один элемент схемы может принадлежать разным цепям, то в общем случае

.

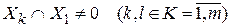Количество связей между некоторым подмножеством 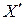вершин гиперграфа и его дополнением 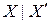подсчитывают как число ребер для которых выполняется условие

;

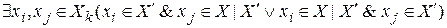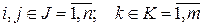. (3.2)

Отсюда видно, что по гиперграфу можно точно оценить число электрических соединений между частями или элементами схемы. Например, схема (рис. 3.1) интерпретируется гиперграфом (рис. 3.7).

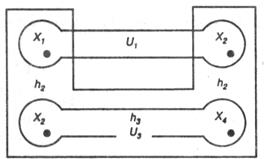
Рис. 3.7 – Гиперграф схемы

Множество вершин этого гиперграфа составляет 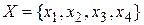, множество ребер определяется, как ; ; .

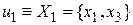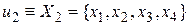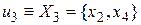Число электрических цепей, соединяющих элементы 1 и 3 с остальными, будет равно единице. Подсчет числа ребер гиперграфа, для которых выполняется условие (3.2), при 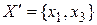, дает такое же значение. При матричном представлении модели схемы в виде гиперграфа принадлежность i-го элемента схемы j-й электрической цепи с точностью до вывода элемента можно задать, если элементы матрицы определять но правилу:

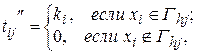
где 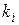— номер вывода i-го элемента схемы. Матрица схемы:

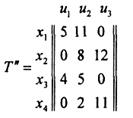
Идентификацию элементов с точностью до вывода при аналитическом представлении гиперграфа можно обеспечить присваиванием весов, характеризующих эти выводы, вершинам, входящим в ребра. Рассматриваемый гиперграф будет представлен массивами

; ;

; ; ;

.

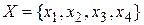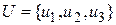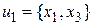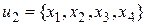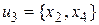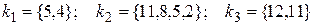причем 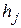поставлено во взаимно однозначное соответствие 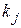. Из гиперграфа с помощью соответствующих преобразований можно получить модель схемы в виде неориентированного мультиграфа [20,37].

При представлении схемы ультраграфом множеству элементов схемы ставится во взаимно однозначное соответствие множество вершин X, а множеству электрических цепей — множество ребер U. Направление передачи сигналов в такой модели схемы задается таким образом: пусть i-й элемент схемы принадлежит j-й цепи, тогда бинарное отношение инцидентности задано на паре 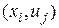, если 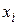сопоставлено с элементом как источником сигнала, и 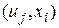— если 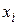интерпретирует элемент как приемник сигнала (рис. 3.8).

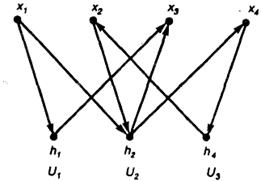
Рис. 3.8 – Кенигово представление ультраграфа схемы

Отображение схемы с точностью до выводов элементов обеспечивается введением весов, характеризующих эти выводы. При задании ультраграфа в виде множеств X, U и отображения U в X весами вершин, входящих в 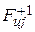и 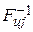, — установлены номера контактов элементов, сопоставленных с этими вершинами. Данная схема описана следующими массивами:

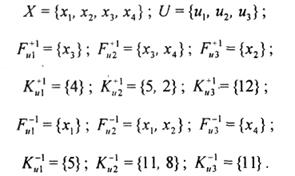
При матричном представлении элементы матрицы определяются по правилу

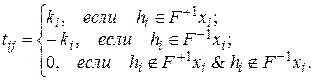
Такая матрица для схемы имеет вид

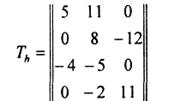
Ультраграф, как и гиперграф, учитывает фактор неизвестности соединений и позволяет точно оценить число электрических соединений [26, 49]. Для всех рассмотренных моделей не выполняется требование информационной полноты. В наибольшей степени оно удовлетворяется, когда схема представляется ультраграфом, при наличии дополнительных сведений о конструктивно-технологических характеристиках элементов и их логических функциях. При интерпретации элементов схемы вершинами графа эти сведения для всех моделей могут быть заданы в виде весовых характеристик вершин. Топологические свойства элементов схемы не отображены ни в одной из рассмотренных моделей.

При представлении схемы в виде неориентированного мультиграфа и гиперграфа не удовлетворяется требование однозначности перехода от модели к схеме. Теория неориентированных и ориентированных графов развита достаточно хорошо. Разработано большое количество алгоритмов решения задач схемно-топологического конструирования методами теории графов. Математический аппарат теории гиперграфов и ультраграфов в настоящее время только развивается.