Модель схемы в виде неориентированного мультиграфа

Чтобы задать информацию о связанности элементов или их выводов, каждая элементарная цепь (комплекс) интерпретируется полным подграфом, что приводит к избыточности ребер, количество вершин подграфа определяется числом элементов или выводов, соединяемых данной цепью. При этом учитывается фактор неизвестности соединения, так как покрывающие «деревья», построенные на полном подграфе, соответствуют возможным вариантам соединения элементов данной цепью. Модель схемы получается объединением полных подграфов.

При такой интерпретации применяется вероятностный подход — каждому ребру 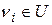полного подграфа присваивают вес:

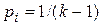, (3.1)

где k— количество вершин полного подграфа.

Модель схемы представлена на рис. 3.1, где & — логическое И; MS — селектор-мультиплексор (выбор канала со стробированием и непрерывная передача информационных посылок в одну линию); ML — мультиплексор (демультиплексор или аналоговый коммутатор). При сопоставлении элементов схемы и вершин графа, получаем граф (рис. 3.2).

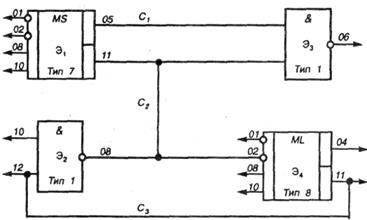
Рис. 3.1 – Модель схемы

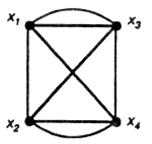
Рис. 3.2 – Граф Рис. 3.3 – Фиксированное дерево

Введение избыточных ребер может сделать граф не пленарным, хотя интерпретируемая нами схема — планарна. По данному графу нельзя получить правильную оценку элементарных связей между частями схемы. Например, количество ребер, попадающих в разрез между 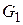и графа G, , равно четырем (для вероятностного графа сумма весов ребер равна 4/3), в то время как в схеме в этом случае разрезается одна цепь. При такой модели схемы существует сильная корреляционная связь между показателями, так что оптимизация одного приводит к оптимизации другого (рис. 3.3).

При сопоставлении выводов элементов и вершин графа граф схемы распадается на отдельные компоненты связности (рис. 3.4), количество которых определяется числом электрических цепей схемы. Объединяя эти компоненты связности в соответствии с принадлежностью выводов элементам схемы, получим рассмотренную выше модель.

Модель схемы, полученную объединением полных подграфов, можно не использовать для решения задач размещения элементов (информацию о метрических параметрах элементов можно учитывать в весовых характеристиках вершин) и компоновки алгоритмами, в которых определяющим является фактор связности. Модель схемы в виде отдельных компонентов связности несет информацию о соединяемых выводах элементов для задачи трассировки [33].

Электрическую цепь можно представить фиксированным «деревом» (см. рис. 3.3), в этом случае не исключаются избыточные ребра, однако не учитывается фактор неизвестности соединений и неверно отражается связность элементов схемы, так как любые две несмежные вершины «дерева» не связаны между собой, в то время как в схеме между соответствующими элементами существует электрическая связь. Такую модель можно использовать для решения топологических задач трассировки, если нет ограничений на проведение соединений под элементами и между их контактами.

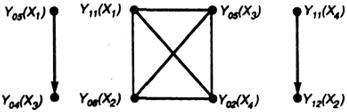
Рис. 3.4 – Компоненты связности