Методы получения моделей элементов вычислительных систем

Получение моделей элементов (моделирование элементов) в общем случае процедура не формализованная. Основные решения при выборе вида математических соотношений, характера используемых переменных и параметров принимает проектировщик. Но операции расчета численных значений параметров моделей, определение областей адекватности алгоритмизированы и решаются на ЭВМ. Поэтому моделирование элементов выполняется специалистами конкретных технических областей с помощью традиционных средств экспериментальных исследований и средств САПР.

Методы получения функциональных моделей элементов делят на теоретические и экспериментальные.

Теоретические методы изучают физические закономерности протекающих в объектах процессов, определяют соответствующее этим закономерностям математическое описание, обосновывают принятие упрощающих предположений, выполняют необходимые выкладки и приводят результаты к принятой форме представления модели.

Экспериментальные методы основаны на использовании внешних проявлений свойств объекта, фиксируемых во время эксплуатации однотипных объектов или при проведении целенаправленных экспериментов [35, 36].

Несмотря на эвристический характер многих операций моделирования, имеется ряд положений и приемов, общих для получения модели различных объектов. Достаточно общий характер имеют методики макромоделирования, математические методы планирования экспериментов, а также алгоритмы формализуемых операций расчета численных значений параметров и определения областей адекватности [30].

Методика макромоделирования имеет следующие этапы.

1) Определение свойств объекта, которые отображаются моделью.

2) Сбор информации о свойствах моделируемой ВС (справочные данные, аналоги).

3) Получение общего вида уравнений модели (структуры), где возможно оперирование не уравнениями, а эквивалентными схемами, чтобы проще установить физический смысл.

4) Определение численных значений параметров, т. е.:

· использование специфических расчетных соотношений (этап 2);

· решение экстремальной задачи, где в качестве целевой функции выбирается степень совпадения известных значений выходных параметров объекта с результатами использования модели, а управляемыми параметрами являются параметры модели;

· проведение экспериментов и обработка полученных результатов.

5) Оценка точности полученной модели и определение области ее адекватности.

Методы планирования экспериментов. Для целей моделирования используют пассивные и активные эксперименты. В пассивных экспериментах нет возможности выбирать условия опыта по своему усмотрению и устанавливать значения факторов на желаемом уровне. В активных экспериментах опыты проводятся по заранее разработанному плану, выражающему количество опытов и значения факторов в каждом опыте [1,41].

Выбор вида зависимости выходного параметра макромодели 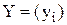от внешних параметров 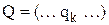осуществляется проектировщиком.

Обычно в методах планирования эксперимента используются линейные модели

Y = AxQ (2.1)

или квадратичные

Y = AxB, (2.2)

где А — вектор-строка коэффициентов (параметров модели);

В — вектор, включающий факторы 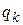, те или иные произведения из двух, трех и более факторов, а так же квадраты факторов 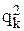, , 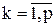где р — число факторов.

Число опытов Nпревышает число определяемых параметров вектора А.Параметры рассчитываются по методу наименьших квадратов, т. е. из условия минимизации суммы квадратов отклонений значений 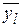определенных по формуле (2.1) и измеренных значений :

,

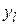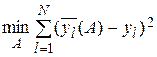где l — номер опыта.

Активный эксперимент имеет преимущества над пассивным:

1) в получении оптимальной области адекватности;

2) в сокращении числа опытов.

Регрессионный анализ. Связь между Y и Q может быть не функциональной, а статистической, что особенно характерно при пассивных экспериментах. Для получения модели в такой ситуации применяют регрессионный анализ. Модель определяют в форме уравнений регрессии (2.1), в которых роль коэффициентов 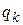в векторе А выполняют коэффициенты относительной регрессии [32, 50].

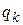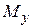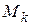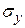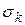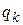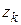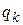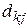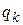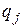Рассмотрим алгоритм вычисления коэффициентов . По результатам пассивных экспериментов получают оценки математических ожиданий , среднеквадратичных отклонений , для выходных y и внешних параметров, а также коэффициенты корреляции между y и образующие вектор R, и коэффициенты корреляции между факторами и образующие матрицу Д. Далее решают систему линейных алгебраических уравнений

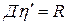(2.3)

и полученный вектор 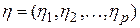используют при расчете относительных коэффициентов регрессии по формуле

.

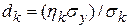Если факторы 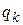не коррелированы, то Д— единичная матрица, и можно обойтись без решения системы (2.3), так как .

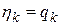Диалоговое моделирование обусловлено наличием эвристических и формальных операций в методике моделирования. Здесь осуществляется оперативный ввод исходной информации о структуре модели, об известных характеристиках и параметрах объекта, о плане экспериментов. В диалоговом моделировании программное обеспечение имеет алгоритмы статистической обработки результатов экспериментов, расчета выходных параметров эталонных моделей и создаваемых моделей, в том числе расчета параметров по методам планирования экспериментов и регрессионного анализа, алгоритмы поиска экстремума, расчета областей адекватности [22, 23]. Пользователь меняет уравнения модели, задает их в аналитической, схемной или табличной форме, общается с подпрограммами, оценивает результаты предпринимаемых действий, приближаясь к получению модели требуемыми свойствами.