Математические модели

Математическое обеспечение включает в себя математические модели (ММ). Основные требования к математическим моделям:

- универсальность характеризует полноту отображения в модели свойств реальной ВС (например, ММ резистора в виде уравнений закона Ома характеризует свойство резистора пропускать электрический ток, но не отражает показатели резистора как детали: его цвет, механическую прочность, стоимость и т. п.);

- точность ММ оценивается степенью совпадения значений параметров реального объекта и значений тех же параметров, рассчитанных с помощью оцениваемой ММ. Допустим, в ММ свойства оцениваются вектором входных параметров 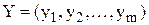Тогда, обозначив истинное и рассчитанное с помощью ММ значение j-го выходного параметра через 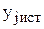и , соответственно определим относительную погрешность 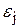расчета параметра 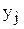как . Получена векторная оценка 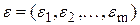. Для скалярной величины используется выражение 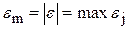, при ;

- адекватность ММ — способность отображать заданные свойства объекта с погрешностью не выше заданной. Адекватность модели имеет место в ограниченной области изменения вектора внешних переменных Q тогда области адекватности (ОА) математической модели определяются по формуле

,

где δ < 0 — заданная константа, равная предельно допустимой погрешности модели;

- экономичность ММ характеризуется затратами вычислительных ресурсов (машинное время и память; размерность ММ, количество параметров).

Классификация ММ:

1) аналитические (в виде уравнений);

2) алгоритмические (выражают связи выходных параметров с параметрами внутренними и внешними в форме алгоритма с численным методом решения);

3) имитационные — алгоритмические модели, отражающие поведение ВС во времени при заданных внешних воздействиях на объект — это модели массового обслуживания, заданные в алгоритмической форме.