Математические модели монтажного пространства

Под монтажным пространством типовой конструкций понимают метрическое пространство, в котором устанавливаются входящие в нее типовые конструкции предыдущих уровней и выполняются электрические соединения выводов. Модель монтажного пространства отображает метрические параметры и топологические свойства конструкции.

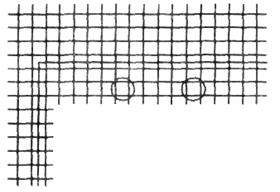
Рис. 3.9 – Верхний слой печатной платы

Метрические параметры — это габаритные размеры зон монтажа, допустимая ширина проводников и зазора между ними, координаты и размеры внешних монтажных площадок, шаг установки и размеры модулей, координаты и размеры полей их контактов.

Топологические свойства — это число слоев монтажной платы и переходов со слоя на слой, наличие замкнутых областей, запрещенных для проведения соединений, ограничения на взаимное расположение соединений в монтажной области и на количество монтажных проводов, подводимых к одному выводу.

В качестве математической модели монтажного пространства используют неориентированный топологический граф (граф решетки). Плоскость монтажного пространства разбивают на элементарные площадки, стороны которых равны шагу проложения проводника по соответствующему направлению (для печатного монтажа элементарная площадка — квадрат). Каждой элементарной площадке ставят в соответствие вершину графа решетки. Две вершины соединены ребром, если между соответствующими элементарными площадками можно провести соединения с учетом метрических и топологических параметров типовых конструкций, устанавливаемых в данном монтажном пространстве.

Модель монтажного пространства может быть представлена фрагментом верхнего слоя печатной платы (рис. 3.9) и фрагментом с ортогональным монтажом при запрещении проведения проводников под микросхемами (рис. ЗЛО). Если проводники разрешается проводить под углом 45°, то каждой вершине может быть инцидентно восемь ребер (рис. 3.11).

Фрагмент математической модели монтажного пространства многослойной печатной платы описывает вертикальные ребра, интерпретирующие межслойные переходы (рис. 3.12).

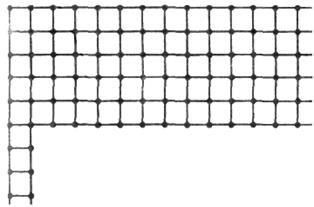
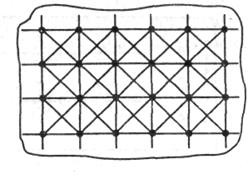
Рис. 3.10 – Модель монтажной плоскости Рис. 3.11 – Модель многосвязной печатной платы

Из множества вершин этого графа можно выделить следующие подмножества: вершины, сопоставленные с контактными площадками выводов модулей (вершины обозначены кружками); вершины, представляющие внешние выводы типовой конструкции, и вершины, интерпретирующие контактные площадки межслойных переходов (вершины обозначены кружками). Фрагмент математической модели монтажного пространства многослойной печатной платы описывает вертикальные ребра, интерпретирующие межслойные переходы.

Из множества вершин этого графа можно выделить следующие подмножества: вершины, сопоставленные с контактными площадками выводов модулей (вершины обозначены кружками); вершины, представляющие внешние выводы типовой конструкции, и вершины, интерпретирующие контактные площадки межслойных переходов (вершины обозначены кружками). В случае выполнения соединений монтажными проводами в любом направлении вершины графа решетки сопоставляют с выводами конструктивного элемента (микросхемы, разъемы соединительной платы и т. п.). Варианты различных соединений представляются полным графом, построенным на этих вершинах (рис. 3.13).

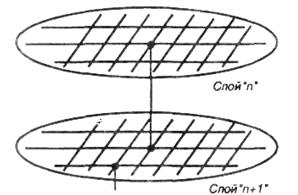
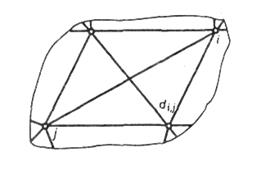
Рис. 3.12 – Модель многослойной Рис. 3.13 – Представление полным
печатной платы подграфом

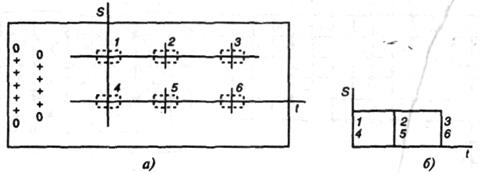
Рис. 3.14 – Граф решетки:
а) регулярного пространства, б) нерегулярного пространства

В конкретной реализации соединений необходимо учитывать ограничения на число проводников, подводимых к одному контакту. Расстояние между i-м и j-м узлами графа решетки в общем случае определяется по формуле

,

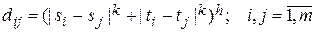где т — число узлов графа решетки. При ортогональной трассировке k=h=1, и получим 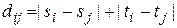. Для регулярного монтажного пространства в качестве модели поля размещения используют граф решетки для платы (рис. 3.14). Приближенный подсчет суммарной длины соединений между модулями можно выполнить следующим образом. Пусть моделью схемы соединения является неориентированный граф G (рис. 3.15), а моделью платы — 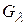граф решетки. Для графа G, преобразованного в решетку 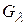(вершины графа располагаются в узлах решетки 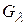), строится матрица расстояний 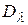, элементы которой подсчитываются по формуле. Если шаги установки модулей по осям s и t равны, расстояния между соседними узлами решетки принимаются равными единице. Матрица расстояний графа

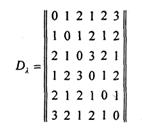
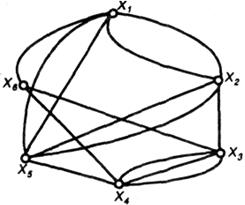
Рис. 3.15 – Неориентированный граф

Суммарная длина ребер графа G, преобразованного в решетку 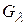, определяется как полусумма элементов матрицы геометрии 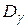. Для получения матрицы геометрии 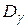необходимо выполнить поэлементное умножение матрицы 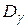и матрицы смежности R графа G. Матрицы смежности и геометрии рассматриваемого графа соответственно будут:

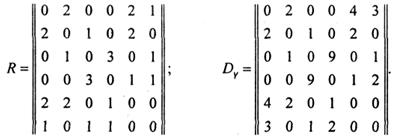
Для данного случая суммарная длина ребер L(G) = 25