Методы расчета и анализа вибраций
Вобщем случае конструкция ВТ представляет собой сложную колебательную систему, состоящую из конечного числа простых механических узлов, обладающих массой 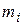 , закрепленных на пружинах с жесткостью
, закрепленных на пружинах с жесткостью 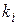 (рис. 4.1).
(рис. 4.1).
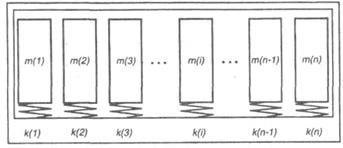
Рис. 4.1. Схема колебательных систем
Эта разбивка конструкции ВТ на простые колебательные системы упрощает методику расчета и анализа воздействия вибраций и является правомерным, так как передвижная ВТ выполняется из блоков, которые жестко укреплены на шасси и связаны гибкими соединениями. Для простой колебательной системы с одной степенью свободы движение под воздействием приложенных сил определяется изменением во времени одной координаты (рис. 4.2).
Такая система состоит из груза массой т, пружины жесткостью k и демпфера с коэффициентом демпфирования b. По принципу Даламбера уравнение движения такой системы относительно положения статического равновесия должно учитывать все силы, действующие на систему, в том числе и силу инерции:
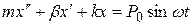 (4.1)
(4.1)
где первое слагаемое в левой части — сила инерции, второе — сила демпфирования, третье — сила упругости пружины; правая часть представляет собой возмущающую силу Р, действующую извне на колебательную систему. Разделив правую и левую части уравнения на т, получим:
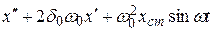 (4.2)
(4.2)
где 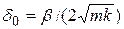 — параметр, пропорциональный коэффициенту демпфирования;
— параметр, пропорциональный коэффициенту демпфирования;
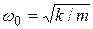 — круговая частота собственных колебаний системы;
— круговая частота собственных колебаний системы;
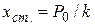 — удлинение (сжатие) пружины, которое она получила бы при статическом воздействии на нее силы
— удлинение (сжатие) пружины, которое она получила бы при статическом воздействии на нее силы 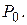
Решим уравнение для свободных и вынужденных колебаний механической системы. Для свободных колебаний правая часть уравнения (4.2) обращается в ноль. Допустим, что в начальный момент времени t = 0 массе т была сообщена мгновенная скорость 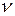 , а затем система начала совершать свободные колебания. Для начальных условий
, а затем система начала совершать свободные колебания. Для начальных условий 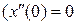 ;
; 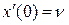 ;
; 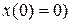 при отсутствии демпфирования
при отсутствии демпфирования 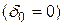 решение уравнения (4.2) имеет вид
решение уравнения (4.2) имеет вид
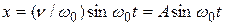 ,
,
т. е. возникает периодическое синусоидальное движение с собственной частотой 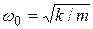 . С увеличением массы частота уменьшается, а с увеличением жесткости пружины
. С увеличением массы частота уменьшается, а с увеличением жесткости пружины 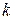 частота увеличивается. Любая реальная система имеет демпфирование
частота увеличивается. Любая реальная система имеет демпфирование 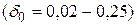 . Так как
. Так как 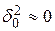 , то решение уравнения (4.2) имеет следующий вид:
, то решение уравнения (4.2) имеет следующий вид:
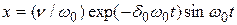 .
.
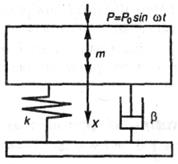
Рис. 4.2. Схема амортизации
Отсюда следует, что при наличии демпфирования 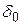 сомножитель
сомножитель 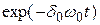 с течением времени стремится к нулю и колебательный процесс прекращается.
с течением времени стремится к нулю и колебательный процесс прекращается.
Если на колебательную систему воздействует внешняя сила Р, то правая часть уравнения (4.1) становится равной 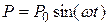 . В этом случае решение уравнения (4.2) приобретает вид
. В этом случае решение уравнения (4.2) приобретает вид
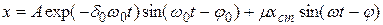 . (4.3)
. (4.3)
Здесь первое слагаемое в правой части уравнения — решение уравнения свободных колебаний, а второе — частное решение, соответствующее гармонической силе Р. При этом
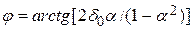 - начальная фаза,
- начальная фаза,
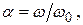 а
а 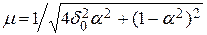 .
.
В уравнении (4.3) только А и 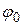 зависят от начальных условий. С течением времени (t → ∞) колебания системы устанавливаются
зависят от начальных условий. С течением времени (t → ∞) колебания системы устанавливаются
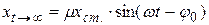
Установившиеся под воздействием внешней гармонической силы колебания называются вынужденными. Характерной особенностью таких колебаний является то, что их амплитуда зависит не только от параметров системы и возмущающей силы, но и от ее частоты 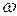 . Если частота возмущающей силы
. Если частота возмущающей силы 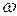 совпадает с собственной частотой системы
совпадает с собственной частотой системы 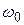 , то наблюдается резонанс. В этом случае решение уравнения (4.1) при нулевых начальных условиях и отсутствии трения будет иметь вид
, то наблюдается резонанс. В этом случае решение уравнения (4.1) при нулевых начальных условиях и отсутствии трения будет иметь вид

т. е. амплитуда колебаний линейно зависит от времени t и частоты собственных колебаний системы. Чем меньше коэффициент 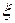 , тем медленнее нарастает амплитуда резонансных колебаний. Отсюда следует, что при быстром прохождении резонансной частоты амплитуда колебаний будет достигать меньшего значения, чем при медленном прохождении резонанса.
, тем медленнее нарастает амплитуда резонансных колебаний. Отсюда следует, что при быстром прохождении резонансной частоты амплитуда колебаний будет достигать меньшего значения, чем при медленном прохождении резонанса.
Если на систему в момент времени t = 0 действуют затухающие колебания, то уравнение движения системы принимает вид
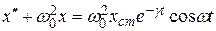 , (4.4)
, (4.4)
где 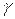 — коэффициент затухания
— коэффициент затухания 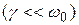
Решением уравнения (4.4) будет равенство
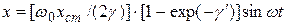 .
.
Тогда амплитуда установившихся вынужденных колебаний на резонансной частоте
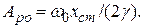
Для системы с трением 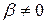 амплитуда колебаний при резонансе может быть определена по выражению
амплитуда колебаний при резонансе может быть определена по выражению
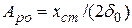
Основные параметры, которыми обычно характеризуют гармонические колебания блоков, следующие: f — частота, Гц; 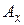 — амплитуда перемещения, мм;
— амплитуда перемещения, мм; 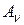 — амплитудное значение скорости, м/с;
— амплитудное значение скорости, м/с; 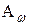 — амплитудное значение ускорения, м/с2;
— амплитудное значение ускорения, м/с2; 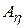 — скорость нарастания ускорения или динамическая перегрузка, м/с3. Все эти параметры связаны между собой соотношениями:
— скорость нарастания ускорения или динамическая перегрузка, м/с3. Все эти параметры связаны между собой соотношениями:
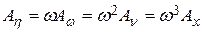 ,
,
где 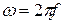 .
.
Движение системы, имеющей 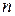 степеней свободы, описывается совокупностью уравнений вида (4.1):
степеней свободы, описывается совокупностью уравнений вида (4.1):
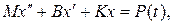
где 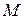 — матрица коэффициентов инерции (масс);
— матрица коэффициентов инерции (масс);
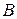 — матрица коэффициентов демпфирования;
— матрица коэффициентов демпфирования;
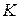 — матрица сил упругости;
— матрица сил упругости;
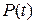 — n-мерный вектор-столбец обобщенных возмущающих сил;
— n-мерный вектор-столбец обобщенных возмущающих сил;
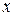 — обобщенная координата.
— обобщенная координата.
Дата добавления: 2015-10-29; просмотров: 1096;
