Критерии надежности

Расширение выполняемых функций и повышение точности работы аппаратуры ВТ, как правило, приводит к ее усложнению, а это ведет к увеличению числа различных элементов, и, как следствие, к снижению надежности работы. Для электронной аппаратуры характерно то, что неисправность одного элемента влечет за собой отказ всего устройства.

Под надежностью устройства или его отдельных блоков понимают способность устройства выполнять заданные функции в течение требуемого интервала времени при определенных условиях эксплуатации. Надежность является важнейшим техническим параметром аппаратуры ВТ, поэтому значение надежности необходимо указывать в технических условиях.

Используя теорию вероятности и математическую статистику для оценки надежности, еще нельзя с абсолютной точностью установить надежность конкретного устройства или время его безотказной работы, но можно предвидеть вероятность безотказной работы в течение определенного времени, интенсивность отказов и т. д.

Отказ — это такое событие, которое ведет к невозможности использования рабочих свойств изделия. Отказы бывают внезапные и постепенные. При внезапных отказах происходит скачкообразное изменение одного или нескольких параметров до уровня, при котором нарушается нормальная работа аппаратуры (это обрыв провода, пробой транзистора, диода и т. д.). Постепенные отказы происходят в результате развития процессов износа и старения. Постепенные отказы носят не случайный, а закономерный характер, и их появление можно заранее предвидеть и предотвратить. Наряду с внезапными и постепенными отказами необходимо учитывать сбои и перемежающиеся отказы.

Сбои — это отказы, возникающие однократно (влияние различных помех и т. д.). Перемежающиеся отказы — это сбои, появляющиеся внезапно, но способные появиться вновь (замыкание электродов электровакуумных приборов в результате их нагрева).

Интенсивностью отказов называют отношение числа отказавших изделий в единицу времени к среднему числу изделий, которые продолжают работать,

,

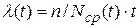где n — число изделий, отказавших за время t;

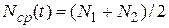— среднее число изделий, исправно работающих в интервале времени t;

N₁ — число исправно работающих изделий в начале интервала времени;

N₂ — число изделий, исправно работающих в конце интервала времени.

Средним временем исправной работы изделий называют среднее арифметическое время исправной работы каждого образца.

Если имеется N образцов, время исправной работы которых соответственно равно 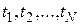, то среднее время исправной работы

.

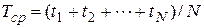Так как установить момент выхода из строя каждого испытуемого образца очень сложно, то на практике T_cp определяют следующим образом:

,

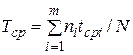где 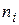— число образцов, вышедших из строя в i-м интервале;

т — число интервалов времени;

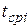— среднее время интервала.

Значение 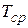часто используют для характеристики надежности устройств, не подлежащих ремонту, т. е. при λ = const. Между интенсивностью отказов и средним временем работы существует обратно пропорциональная зависимость, т. е.

.

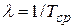Удобным на практике критерием надежности является среднее число часов работы между двумя соседними отказами, обычно называемое наработкой на отказ. Таким образом, если аппаратура проработала суммарное время 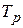часов и имела при этом п отказов в работе, то наработка на отказ

.

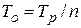Продолжительность времени исправной работы t между любыми двумя соседними отказами является величиной случайной и ее точное значение определить невозможно. Поэтому используется усредненная статистическая величина 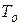, определяемая по данным специальных испытаний на надежность.

Общее время работы аппаратуры 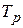за определенный календарный срок равно сумме интервалов рабочего времени между соседними отказами

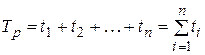
Тогда

,

где п — число отказов за время испытания;

— время исправной работы между i = 1 и i-ми отказами аппаратуры.

Практически установлено, что минимальное число отказов для выявления значения 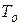должно быть не менее десяти. При экспоненциальном законе распределения надежности наработка на отказ равна среднему времени безотказной работы, т. е. .

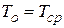Под безотказной работой аппаратуры понимают такую ее работу, когда в заданном интервале времени t при определенных режимах и условиях эксплуатации не произойдет ни одного отказа.

Для аппаратуры, в которой происходят внезапные отказы (действует экспоненциальный закон распределения — закон Пуассона), вероятность безотказной работы до первого отказа в течение времени t определяется по формуле

.

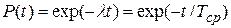Для аппаратуры, в которой происходят постепенные отказы, вероятность безотказной работы

,

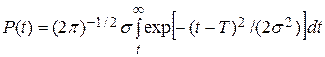где 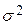— дисперсия среднего времени исправной работы различных экземпляров аппаратуры,

,

где 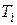, Т — соответственно среднее время безотказной работы i-го и всех экземпляров;

N— количество экземпляров аппаратуры.

Так как аппаратура ВТ состоит из конечного числа блоков (или элементов), то вероятность безотказной работы устройства 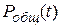определяется вероятностями безотказной работы ее элементов 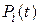. Если предположить, что отказы в элементах независимы друг от друга, то справедливо выражение

,

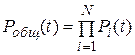где N— число элементов устройства или системы,

.

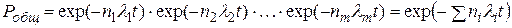Сумма произведений числа элементов и, на интенсивность отказов называется интенсивностью отказов системы

.

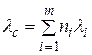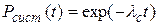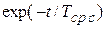Таким образом, или , где 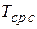— среднее время исправной работы системы.