Расчет отклонений параметров конструкции

Для определения отклонения выходного параметра А блока или изделия необходимо знать исходную зависимость этого параметра от независимых параметров :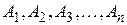

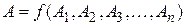. (3.1)

Необходимо также знать отклонения независимых параметров, входящих в блок или данное изделие деталей или блоков: 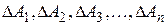. Тогда предполагая, что отклонения параметров малы по сравнению с самими параметрами, для определения максимального абсолютного отклонения функции нескольких переменных (3.1) необходимо просуммировать абсолютные значения произведений частных производных этой функции по каждому аргументу на абсолютное отклонение соответствующего аргумента:

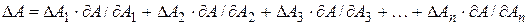. (3.2)

Наиболее показательным является представление об отклонении параметров, когда оно дано в относительных единицах. Тогда выражение (3.2) для относительного отклонения параметра δ можно представить в следующем виде:

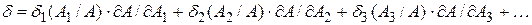
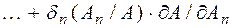. (3.3)

где , , , …,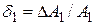

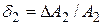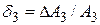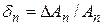
Из выражения (3.3) видно, что:

а) отклонение искомого параметра выражается через сумму слагаемых, каждое из которых является функцией отклонения только одного независимого параметра;

б) каждое слагаемое этого выражения содержит кроме отклонения независимого параметра еще и сомножитель, который определяет степень влияния отклонения данного независимого параметра на искомое отклонение. Это влияние называют коэффициентом влияния или весовым коэффициентом. Эти коэффициенты раскрывают степень и форму взаимосвязи между искомым и независимым параметрами. Они не только позволяют определить отклонения параметров, но и раскрывают сущность взаимосвязи элементов в конструкции. Поэтому выражение (3.3) можно представить в виде

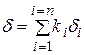, (3.4)

где 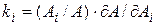; 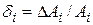. Таким образом, с помощью выражений (3.2) и (3.3) можно определить абсолютное и относительное отклонение выходных параметров, если известны отклонения независимых параметров и их функциональная связь с исследуемым параметром.

Для определения отклонения выходного параметра конструкции пользуются тремя видами значений:

а) предельным абсолютным;

б) предельным относительным;

в) вероятным (среднеквадратическим отклонением).

Предельное абсолютное значение отклонения в основном используется для определения и установления размеров геометрических параметров конструкций. Предельное абсолютное значение отклонения определяется при помощи формулы (3.2) с учетом знаков независимых параметров, но так, чтобы обеспечить максимальное значение отклонения (например, все знаки «+»).

Для простейших и часто встречающихся функций отклонения выходного параметра определяют таким образом:

а) для суммы параметров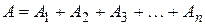

;

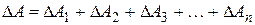б) для произведения параметров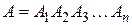

.

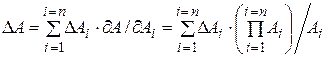Предельное относительное значение отклонения используется чаще всего в определении и установлении электрических параметров элементов и составленных из них электрических цепей. Предельные относительные отклонения параметров определяют при помощи формулы (3.3) с учетом знаков независимых параметров:

а) для суммы параметров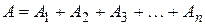

;

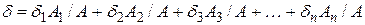б) для произведения параметров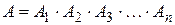

.

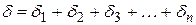Вероятное значение отклонения (среднеквадратическое отклонение) является важным для анализа конструкции и производственного процесса. Оно позволяет определить, какое вероятное количество продукции может быть выпущено с данным конкретным отклонением. Этим можно достичь наиболее эффективного экономического результата, варьируя широтой допускаемого отклонения независимых параметров составляющих конструкции (изделия).