Передача теплоты в электронных устройствах

Процесс передачи теплоты теплопроводностью объясняется обменом кинетической энергией между молекулами вещества и диффузией электронов. Оба эти явления наблюдаются в том случае, когда температура вещества в различных точках различна или когда контактируют два объекта с различной степенью нагрева. Основной закон теплопроводности (закон Фурье) утверждает, что количество теплоты, проходящей через тело в единицу времени, прямо пропорционально площади поперечного сечения, нормальной к потоку теплоты и температурному градиенту вдоль потока:

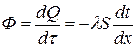, (4.6)

где Q — количество теплоты, Дж;

t — время, с;

t — константа, характеризующая теплопроводность материала Вт/(мК);

X— линейная координата, м.

Из уравнения следует, что поток теплоты может быть направлен только в сторону падения градиента температур. Для случая, когда теплофизические характеристики вещества постоянны во всех точках, а тепловой поток имеет составляющие распространения по трем координатным осям, пользуясь предыдущей формулой, можно записать основное уравнение теплопроводности:

,

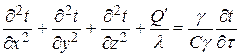где Q’— количество теплоты, эквивалентное мощности внутренних источников в единице объема, Дж;

С — удельная теплоемкость вещества, Дж/(кгК);

g — плотность вещества, кг/м³.

Для случая передачи теплоты через плоскую стенку толщиной b (рис. 4.16) количество теплоты, передаваемой за единицу времени через участок стенки площадью S, на основании закона Фурье (4.6):

,

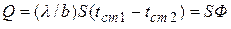где 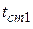, 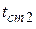— постоянные во времени температуры поверхностей стенки, К или °С.

Если теплопроводность не зависит от температуры, то внутри стенки она убывает по линейному закону.

Отношение b/(lS) называют термическим или тепловым сопротивлением и обозначают

.

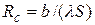Значение 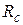соответствует сопротивлению R в уравнении закона Ома, а величина, обратная коэффициенту теплопроводности, т. е. удельное термическое сопротивление Е, эквивалентна удельному сопротивлению в электротехнике:

.

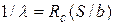Так, для трехслойной стенки (рис. 4.16), пользуясь уравнением (4.6), составим систему уравнений:

.

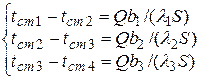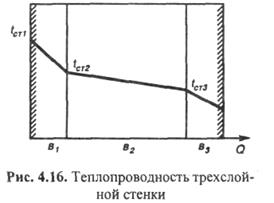
После сложения этих уравнений получим схему (рис. 4.17).

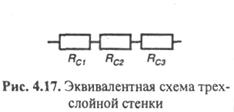
Решив систему уравнений, получим:

.

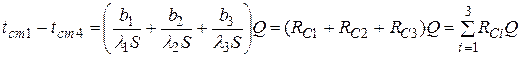Пусть элементы, которые необходимо охлаждать, располагаются на стенке, имеющей температуру

.

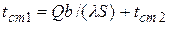Тогда для уменьшения 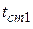следует увеличить площадь теплоотводящей поверхности, уменьшить количество выделяемой теплоты, толщину стенки (путь передачи теплоты), температуру и выбрать материал с высокой теплопроводностью. Этому требованию соответствуют печатные платы на металлической основе.

Естественное и принудительное воздушное охлаждение. Эти способы охлаждения наиболее просты и доступны, так как все элементы микроЭВМ находятся в объеме, заполненном воздухом или инертным газом. Теплота от нагретых корпусов микросхем передается окружающей атмосфере за счет естественной конвекции. Эффективность естественного воздушного охлаждения тем больше, чем больше разность температур между корпусом и окружающей средой и чем больше площадь поверхности корпуса. Большое значение также имеет плотность окружающей среды, при уменьшении которой отвод теплоты от поверхности корпуса уменьшается.

В общем случае тепловое сопротивление 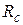с учетом 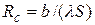имеет вид

.

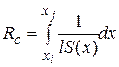Так как элементы конструкции имеют разную форму, то выражения для теплового сопротивления однородных тел плоской 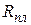(рис. 4.18, а), цилиндрической 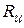(рис. 4.18, б) и шаровой 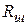(рис. 4.18, в) конфигурации имеют такой вид:

,

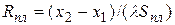где 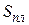— площадь плоской стенки;

,

.

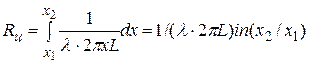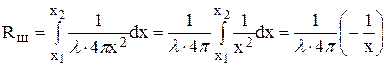Напомним, что теплообмен конвекцией описывается законом Ньютона — Римана: Ф=aSDt, согласно которому тепловой поток от поверхности твердого тела к среде или наоборот будет иметь вид

,

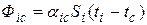где 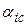— коэффициент теплообмена конвекцией между поверхностью тела и средой, Вт/(мТрад);

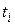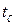и — температура поверхности тела и среды;

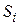— площадь поверхности теплообмена, м².

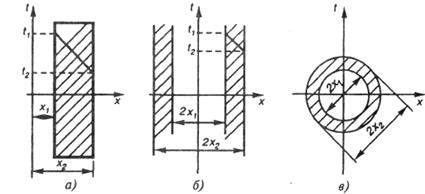
Рис. 4.18. Элементы конструкции

Если тепловая энергия передается от поверхности i к поверхности j через жидкую или газообразную прослойку, тогда тепловой поток

,

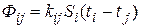где 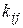— коэффициент теплопередачи в прослойке, Вт/(м²-К).

Коэффициенты теплообмена конвекцией 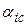и теплопередачи в прослойке 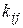являются функциями физико-механических и кинематических свойств жидкости или газа, а также параметров, характеризующих форму и размеры поверхностей. При анализе процессов теплообмена конвекцией используют критерии:

Нуссельта ;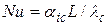

Грасгофа ;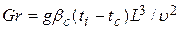

Прандтля ;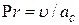

Рейнольдса ,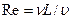

где L — определяющий размер элемента конструкции (длина обтекания, длина пластины или цилиндра);

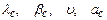— соответственно коэффициенты теплопроводности, объемного расширения (жидкости или газа), 1/К, кинематической вязкости, м²/с, температуропроводности, м²/с;

g — ускорение свободного падения, м/с²;

n — скорость потока жидкости или газа, м/с.

При построении тепловой модели упрощают элементы конструкции и идеализируют протекающие в них тепловые процессы. Один из способов упрощения — замена сложной по форме нагретой зоны элемента конструкции прямоугольным параллелепипедом — эквивалентом нагретой зоны с одинаковой среднеповерхностной температурой и равномерно распределенным источником тепловой энергии. Такая замена выполняется на основе принципа усреднения. Идеализация тепловых процессов заключается в том, что учитываются только основные, вносящие наибольший вклад в тепловой обмен, способы переноса тепловой энергии. Упрощение элементов конструкции и идеализация тепловых процессов должны быть таковы, чтобы обеспечивалась адекватность модели.

Тепловые процессы при таком подходе описываются системой неоднородных нелинейных алгебраических уравнений, которые составляются на основе закона сохранения энергии с использованием выражения

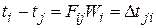
где 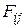— тепловой коэффициент,

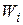— перенос тепловой энергии от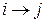

Число уравнений определяется количеством нагретых зон.