Основы теории потенциала электрического поля

Введем при помощи электродов А и В электрический ток в проводящую среду и рассмотрим создаваемое при этом электрическое поле. Это поле так же,как и электростатическое, характеризуется напряженностью, потенциалом и изображается в виде силовых линий и эквипотенциальных поверхностей.

Силовые линии в электростатическом поле соответствуют путям, вдоль которых должен был бы двигаться положительный заряд, а в проводящей среде по этим линиям происходит фактическое перемещение зарядов, которые являются таким образом токовыми линиями.

Сила тока i представляет собой физическую величину, измеряемую количеством электричества, перенесенного через данную площадку в единицу времени, независимо от того, в каком направлении и под каким углом к площадке движутся частицы, несущие заряды.

Для учета направления переноса зарядов вводится в рассмотрение вектор плотности тока j, который направлен в сторону движения положительных зарядов, т. е. в направлении вектора напряженности Е.

Под плотностью тока понимается количество электричества, протекающее в единицу времени через единичную площадку, перпендикулярную к направлению тока.

Если ток i равномерно распределен по площади S, перпендикулярной к его направлению, то величина плотности тока j равна

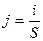(7)

В общем случае плотность тока определяется отношением силы тока ∂i, протекающей через перпендикулярный к направлению тока элемент сечения среды, к площади ∂Sэтого элемента

(8)

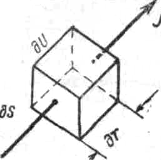
Рис.8

Для пояснения первого закона выделим элементарный объем (рис. 8) среды с удельным сопротивлением ρ_n, длиной ∂r и сечением ∂S; через сечение ∂S и перпендикулярно ему проходит ток ∂i, образуя на концах падение потенциала ∂U.

Согласно формуле 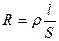сопротивление элементарного объема будет

,

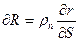а падение потенциала на его концах или

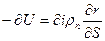
или

Пользуясь уравнениями (5) и (8), получаем

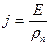(9)

Закон Ома в дифференциальной форме выражается так: плотность тока в каждой точке проводника равняется напряженности электрического поля в этой точке, деленной на удельное сопротивление вещества.

Физическая сущность первого закона Кирхгофа в дифференциальной форме заключается в том, что если какой-либо элемент объема не содержит источников, то сила тока, втекающего в этот объем, равна силе тока, вытекающего из него.

Этим выражается непрерывность потока токовых линий через любую замкнутую поверхность, не содержащую дополнительных источников тока.

Если считать, что входящие и выходящие из данного объема токи имеют разные знаки, то алгебраическая сумма их равна нулю, т. е. эти токи по величине равны.

Невыполнение этого условия привело бы к накоплению электрических зарядов в некоторых точках, что исключается.

Закон Кирхгофа в дифференциальной форме записывается в виде следую­щего дифференциального уравнения:

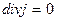(10)

В частном случае однородных и изотропных сред это уравнение преобра­зуется в дифференциальное уравнение Лапласа

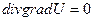(11)

которое в прямоугольной системе координат принимает следующий вид:

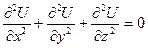(12)

где x, у, z — координаты некоторой точки, в которой определяется элек­трическое поле.

Уравнение (12) так же,как и уравнение (10), справедливо для всех точек поля, которые не содержат источников тока.

Если имеются среды I и II, обладающие удельными сопротивлениями, соответственно равными ρ₁ и ρ₂, и потенциалами U₁ и U₂, разграниченные некоторой поверхностью, то задачу определения потенциала можно решить при помощи уравнения Лапласа при выполнении следующих граничных условий:

а) равенство потенциалов U₁ = U₂, устанавливающее непрерывность потенциального поля во всем изучаемом пространстве;

равенство нормальных составляющих плотности тока

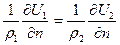(13)

где 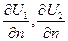- производные от потенциала по нормали к поверхности, указывающие на непрерывность нормальных составляющих вектора плотности тока.