Электрическое поле в однородной изотропной среде
 |
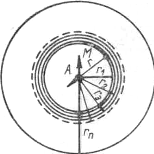Предположим, что имеется однородная изотропная среда с удельным сопротивлением ρ. Введем в эту среду электрод А, из которого вытекает ток силой i. Допустим, что размеры электрода А малы и электрод можно рассматривать как точечный, а второй электрод удален (теоретически в бесконечность) и не оказывает влияния на электрическое поле вблизи электрода А.
Рис. 9 Электрическое поле в однородной изотропной среде.
При этих условиях линии тока, исходящие из точки А, будут прямыми, а эквипотенциальные поверхности — концентрическими сферами с центром в точке А. В пересечении с плоскостью чертежа эти сферы дают окружности с центром в точке А (рис. 9).
Определим потенциал в точке М, расположенной на расстоянии г от источника тока.
Плотность j в точке М согласно формуле (7) равна:
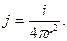(14)
Так как: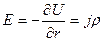 
,
то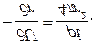 
Зная это, потенциал в точке М можно вычислить так:
.
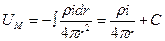Так как потенциал в бесконечности равен нулю, т. е. при г =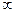 
U = 0, то постоянная интегрирования С = 0. Тогда выражение потенциала в точке М, созданного точечным электродом А, через который протекает ток i, в однородной изотропной среде с удельным сопротивлением ρ примет вид:
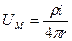(15)
Легко видеть, что если поменять местами точки А и М, т. е. источник тока поместить в точку М и определять потенциал в точке А, то его величина выражается тем же уравнением (15). Это положение справедливо также для неоднородной среды и находит важное практическое применение в электрическом каротаже, которое известно под названием принципа взаимности.
Дата добавления: 2015-10-29; просмотров: 1684;