Уравнения равновесия элементарного параллелепипеда и элементарного тетраэдра

Выделим у исследуемой точки А (с координатами х, у и z) напря­женного упругого тела тремя взаимно перпендикулярными па­рами плоскостей элементарный параллелепипед с размерами ребер dx, dy и dz (рис. 2). По каждой из трех взаимно перпен­дикулярных граней, примыкающих к точке А (ближайших к пло­скостям координат), будут действовать три составляющих напря­жения - нормальное и два касательных. Считаем, что по граням, примыкающим к точке А, они положительны.

При переходе от грани, проходящей через точку А, к парал­лельной грани напряжения меняются и получают приращения. Например, если по грани CAD, проходящей через точку А, дей­ствуют составляющие напряжения 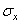= f₁ (x,y,z), 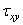=f₂(x,y,z,), 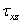=f₃ (x,y,z,), то по параллельной грани, вслед­ствие приращения только одной координаты х при переходе от одной грани к другой, будут действовать составляющие напря­жения 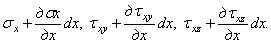Можно определить напряжения на всех гранях элементарного паралле­лепипеда, как показано на рис. 3.

Кроме напряжений, приложенных к граням элементарного параллелепипеда, на него действуют объемные силы: силы веса, инерционные. Обозначим проекции этих сил, отнесенных к единице объема, на оси координат через X, У и Z. Если приравнять нулю сумму проекций на ось х всех нормальных, касательных и объемной сил, дейст­вующих на элементарный параллелепипед, то после сокращения на произведение dxdydz получим уравнение

.

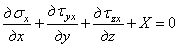Составив аналогичные уравнения проекций сил на оси у и z, напишем три дифференциальных уравнения равновесия элементар­ного параллелепипеда, полученных Коши,

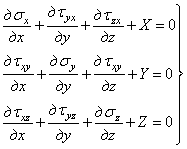. (1.2)

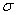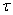При уменьшении размеров параллелепипеда до нуля он прев­ращается в точку, а и представляют собой составляющие напряжения по трем взаимно перпендикулярным площадкам, проходящим через точку А.

Если приравнять нулю сумму моментов всех сил, действующих на элементарный параллелепипед, относительно оси x_c, парал­лельной оси х и проходящей через его центр тяжести, получим уравнение

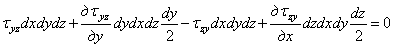
или, с учетом того, что второй и четвертый члены уравнения выс­шего порядка малости по сравнению с остальными, после сокра­щения на dxdydz

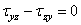или .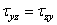

Составив аналогичные уравнения моментов относительно цен­тральных осей у_c и z_c , получим три уравнения закона парности касательных напряжений

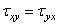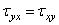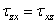, , .(1.3)

Этот закон формулируется так: касательные напряжения, действующие по взаимно перпендикулярным площадкам и направ­ленные перпендикулярно к линии пересечения площадок, равны по величине и одинаковы по знаку.

Таким образом, из девяти составляющих напряжений матрицы тензора 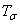шесть попарно равны друг другу, и для определения напряженного состояния в точке достаточно найти лишь следую­щие шесть составляющих напряжений:

.

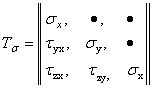Но составленные условия равновесия дали нам всего лишь три уравнения (1.2), из которых шесть неизвестных найдены быть не могут. Таким образом, прямая задача определения напряжен­ного состояния в точке в общем случае статически неопределима. Для раскрытия этой статической неопределимости необходимы дополнительные геометрические и физические зависимости.

Рассечем элементарный параллелепипед у точки А плоскостью, наклоненной к его граням; пусть нормаль N к этой плоскости имеет направляющие косинусы l, т и п. Полу­чившаяся геометрическая фигура (рис. 4) представляет собой пирамиду с треугольным основанием - элементарный тетраэдр. Будем считать, что точка А совпадает с началом координат, а три взаимно перпендикулярные грани тетраэдра - с плоскостями координат.

Составляющие напряжения, действующие по этим граням тетраэдра, будем считать положительными. Они показаны на рис. 4. Обозначим через 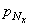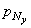и 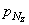проекции полного напря­жения p_N , действующего по наклонной грани BCDтетраэдра, на оси х, у и z. Площадь наклонной гра­ни BCD обозначим dF. Тогда площадь грани АВС будет dF 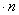, грани ACD - dF 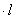и грани АDВ - dF .

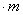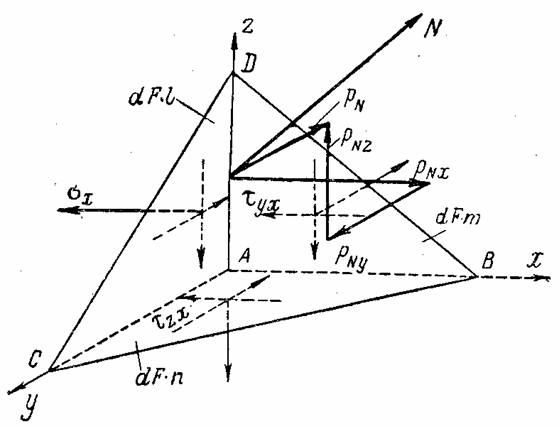
Рис. 4

Составим уравнение равновесия тетраэдра, спроектировав все силы, действующие по его гра­ням, на ось х; проекция объемной силы в уравне­ние проекций не входит, так как представляет собой величину высшего порядка малости по сравнению с проекциями поверхностных сил:

,

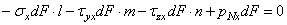откуда

.

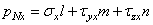Составив уравнения проекции сил, действующих на тетраэдр, на оси у и z, получим еще два аналогичных уравнения. В результате будем иметь три уравнения равновесия элементар­ного тетраэдра

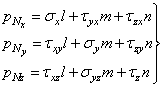. (1.4)

По известным трем проекциям найдем полное напряжение

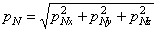. (1.5)

Разделим пространственное тело произвольной формы систе­мой взаимно перпендикулярных плоскостей хОу, yОz и хОz (рис. 5) на ряд элементарных параллелепипедов. У поверхности тела при этом образуются элементарные тетраэдры, (криволинейные участки по­верхности ввиду их малости можно заменить плоскостями). В та­ком случае р_N будет представлять нагрузку на поверхности, а уравнения (1.4) будут связывать эту нагрузку с напряжениям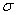и и 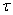в теле, т. е. будут представлять граничные условия задачи теории упругости. Условия, определяемые этими уравнениями, называют условиями на поверхности.

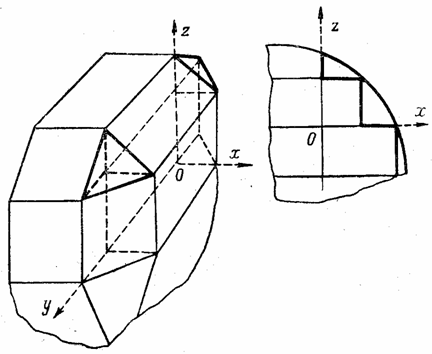
Рис. 5

Следует отметить, что в теории упругости внешние нагрузки представляются нормальными и касательными напряжениями, приложенными по какому-либо закону к площадкам, совпадаю­щим с поверхностью тела.