Определение эластичности цепной одинарной контактной подвески

Эластичность под струной в средней части пролета цепной контактной подвески можно определить, пользуясь теми же рассуждениями, которые мы применили для простой подвески. Расчетная схема приведена на рисунке 87.

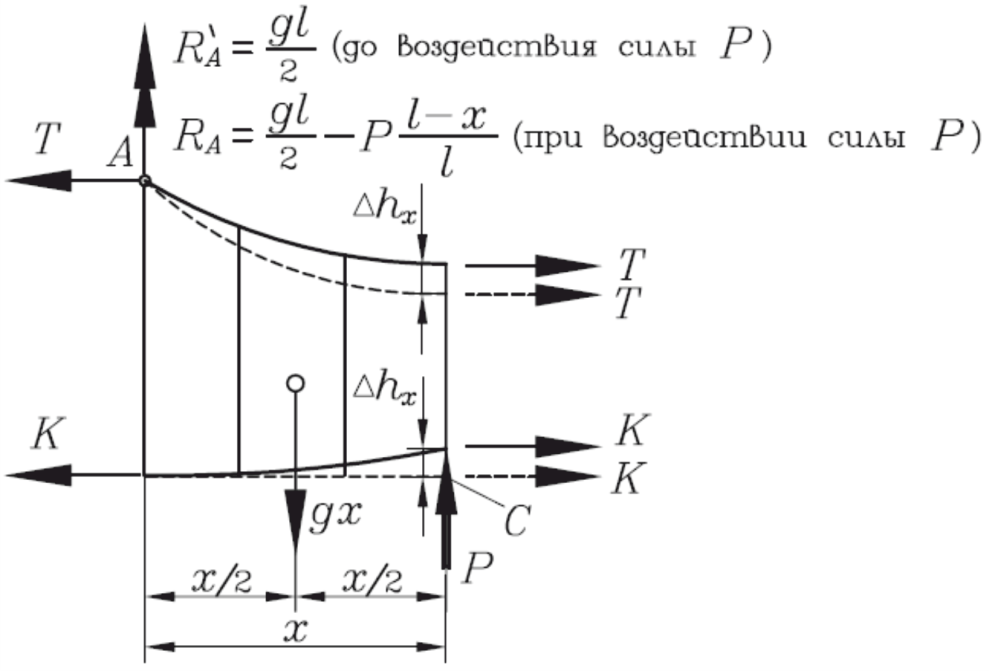
Рисунок 87 – Расчетная схема для определения эластичности цепной одинарной контактной подвески с заменой правой части пролета реакциями

Если считать, что под воздействием силы P струна не разгружаются, подъем (отжатие) контактного провода на высоту ∆h_x повлечет за собой подъем и несущего троса на ту же высоту ∆h_x.

Можно записать два уравнения равновесия для рассматриваемой части пролета до и после приложения силы, а потом вычесть из одного уравнения другое, как мы сделали для простой подвески. А можно сразу записать уравнение для суммы изменений моментов сил относительно точки C, и приравнять ее нулю:

(156)

откуда получаем выражение для подъема

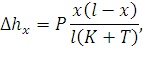
(157)

и выражение для эластичности:

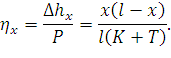
(158)

Эластичность в середине пролете найдем, подставив в (158) x=l/2:

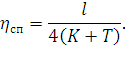
(159)

Эти уравнения мы уже приводили без вывода. Еще раз обратим внимание, что они справедливы для эластичности под струной в средней части пролета, если струны не разгружаются.

Между струнами эластичность цепной одинарной подвески складывается из эластичности системы «несущий трос – контактный провод» и эластичности контактного провода в межструновом пролете.

В общем виде расчетная формула для определения эластичности цепной подвески может быть представлена выражением

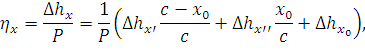
(160)

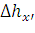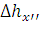где и – подъем контактных проводов под ближайшими к точке приложения силы P нагруженными струнами, м;

c – длина межструнового пролета (между ближайшими к точке приложения силы P нагруженными струнами), ;

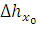– отжатие контактного провода в межструновом пролете (между двумя нагруженными струнами), м;

x₀ – расстояние от левой нагруженной струны до силы P, м.

Значение отжатия контактного провода в межструновом пролете 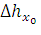находится по формуле, выведенной нами для свободно подвешенного провода (153), необходимо лишь заменить обозначения

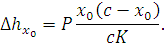
(161)

Для определения 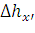и 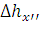в различных точках пролета рессорных цепных подвесок применяют три группы расчетных формул: для зоны расположения подрессорных струн (А), для зоны установки первой от опоры простой (нерессорной) струны (Б) и для средней части пролета (В).

Для вывода расчетных формул отжатий контактного провода и эластичности в средней части пролета (зона В) одинарных цепных рессорных и с простыми опорными струнами подвесок можно воспользоваться расчетной схемой, приведенной на рисунке 88.

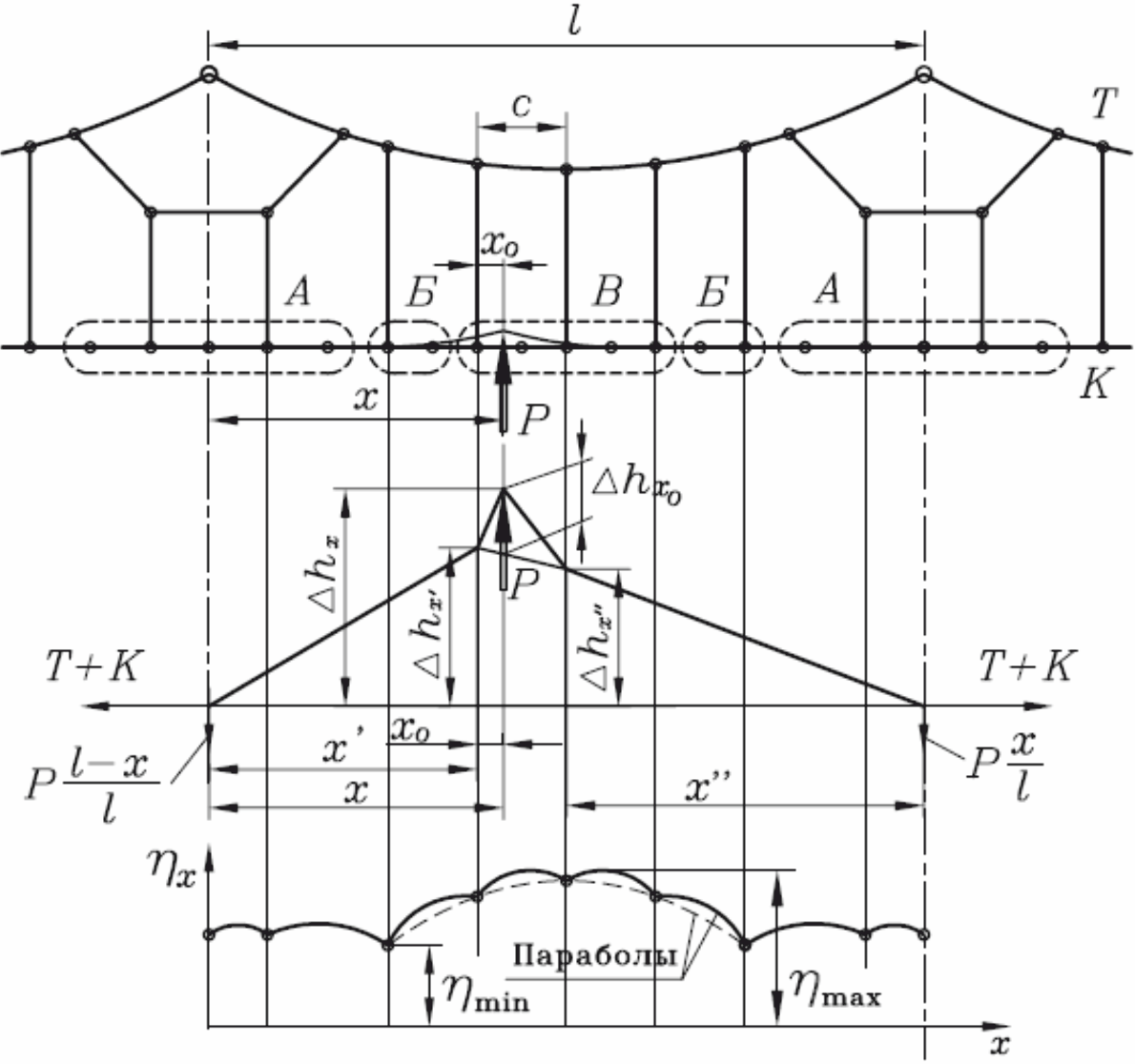
Рисунок 88 – Расчетная схема для определения эластичности контактной подвески с рессорным тросом и отжатий контактного провода

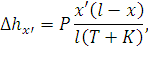
(162)

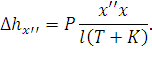
(163)

Подставив эти формулы в выражение (160), после преобразований, получим общую формулу для определения эластичности цепной подвески в средней части пролета (зона В):

(164)

Отметим, что под струнами эта формула превращается в (158).

Таким образом, на самом деле, в средней части пролета распределение эластичности представляет собой картину, показанную на рисунке 88: точки соответствующие струнам расположены на «большой параболе», между струнами – «маленькие параболы».

Эластичность в середине пролета, если там установлена струна, определяется уже выведенным выражением (159), которое получается и из (164), если x=l/2 и x₀=0:

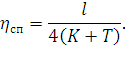
(165)

Если струны расположены так, что в середина пролета подвески совпадает с серединой межструнового пролета (x=l/2, x⁰=c/2),

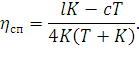
(166)

Для выравнивания эластичности выгодно снизить эластичность в середине и поставить в середине пролета струну.

Расчетные формулы для зон А и Б, мы выводить не будем (это достаточно сложно, кроме того в эти формулы входят коэффициенты, полученные экспериментальным путем).

Все расчетные формулы для всех зон А, Б и В получают в трех вариантах: до разгрузки струн, при разгрузке одной струны, при разгрузке еще и соседних струн. Поэтому вначале находят силы, при которых разгружаются струны и сравнивают их с приложенной силой, после чего выбирают соответствующие формулы. Данная методика и расчетные формулы приведены в [2].

В настоящее время, благодаря развитию компьютеров, в расчетах все более широко применяют программы, построенные на основе математического моделирования методом конечных элементов.

Для расчетов параметров контактной подвески и моделирования ее взаимодействия с токоприемниками такие программы разработаны в Уральском государственном университете путей сообщения (УрГУПС), а также в «Универсал – контактные сети».

В качестве примера на рисунке 89 кривую распределения эластичности для нерессорной компенсированной контактной подвески КС-200-25 в пролете со средней анкеровкой, построенную программой, в которой реализован метод конечно-элементного моделирования.

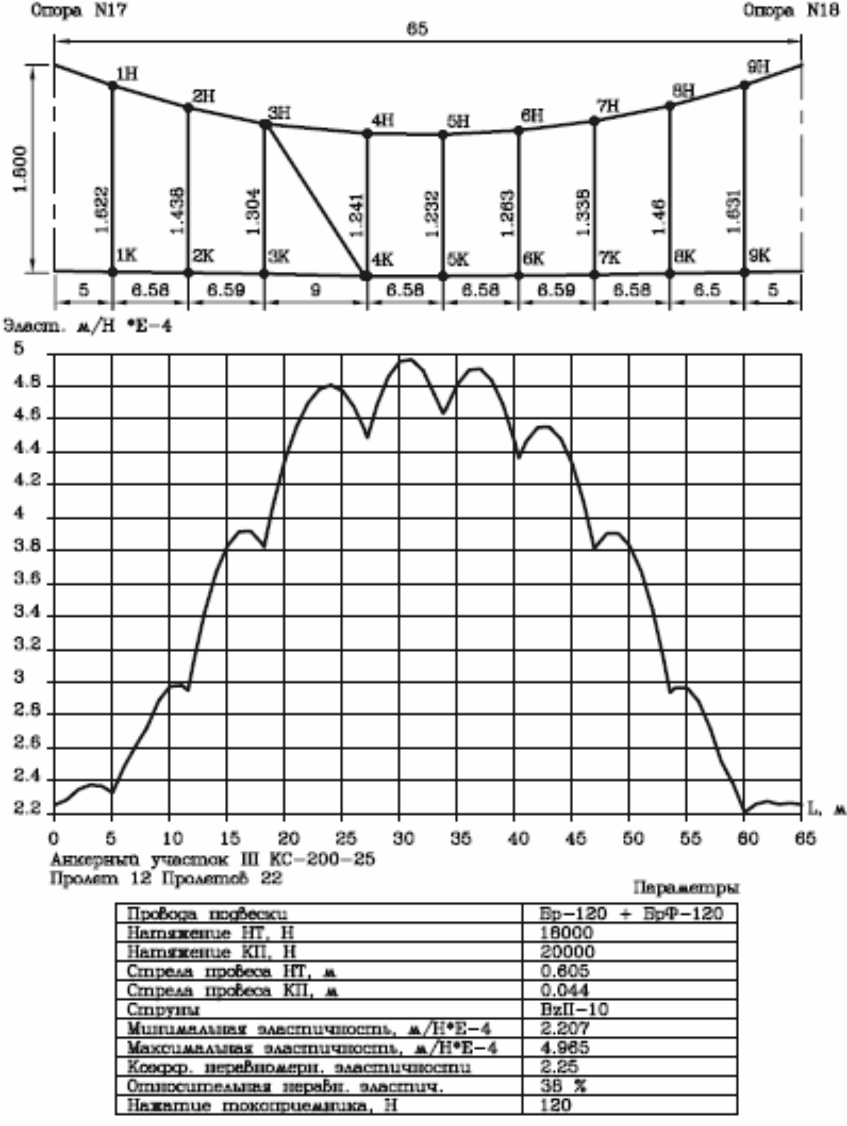
Рисунок 89 – Кривая распределения эластичности для нерессорной компенсированной контактной подвески КС-200-25

Отметим, что в расчете учитывается увеличение эластичности в межструновых пролетах («параболы на параболе»). Программа позволяет учесть сосредоточенные массы на проводах (например, зажимы), параметры фиксаторного узла, дополнительные конструкции – тросы средней анкеровки, электрические соединители и т.д.

5.1.3. Выравнивание траектории точки контакта токоприемника с контактным проводом в пролете. Оптимальные параметры подвески

Вопрос «зачем нужно заниматься выравниванием траектории точки контакта токоприемника с контактными проводом?» мы уже обсуждали. Чем ближе траектория движения токоприемника к прямолинейной (т.е. чем меньше размах колебаний), тем меньше будут вертикальные ускорения точки контакта, а следовательно – тем меньше будут пределы изменения силы контактного нажатия.

Рассмотрим схему пролета одинарной рессорной компенсированной цепной контактной подвески с беспровесным расположением контактного провода и кривую, характеризующую, изменение эластичности в пределах пролета (рисунок 90). Для большей наглядности дальнейших рассуждений кривую изменения эластичности покажем упрощенно, без учета изменения эластичности между струнами.

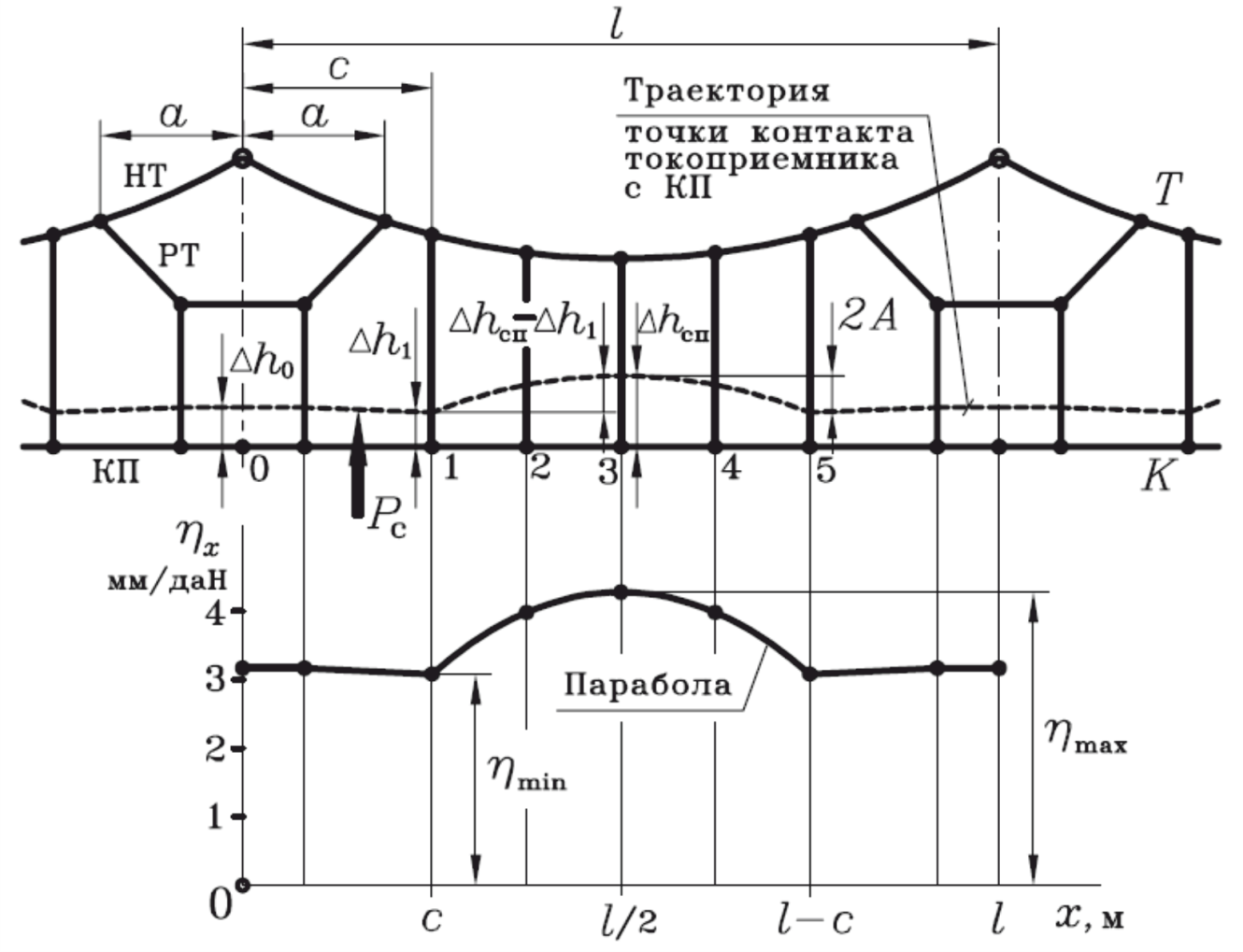
Рисунок 90 – Эластичность пролета одинарной рессорной компенсированной цепной подвески

При скоростях движения ЭПС до 120 км/ч траектория точки контакта токоприемника с контактным проводом в определенном масштабе повторяет кривую изменения эластичности (∆h_x=η_x Pк). Т.е. характер изменения эластичности в пролете определяет характер траектории точки контакта.

Поэтому, в первую очередь, стремятся выравнить траекторию точки контакта за счет выравнивания эластичности в пролете. Этот вопрос мы также уже обсуждали и знаем, что для обычных одинарных подвесок это делается за счет:

1. Увеличения эластичности опорного узла. Для этого мы применяем рессорный трос. Выгодно увеличение длины рессорного троса и его натяжения.

2. Уменьшения эластичности в середине пролета. Мы убедились, что для этого целесообразно устанавливать струну ровно в середине пролета, а поскольку η_сп=l/(4(K+T)) выгодно увеличивать натяжения НТ и КП до максимально допускаемых значений (с учетом коэффициентов запаса по прочности), а также выгодно уменьшить длину пролета, однако это нецелесообразно с экономической точки зрения.

Применяя эти меры, для обычных одинарных рессорных подвесок можно добиться выравнивания эластичности до k_э=η_max/η_min=1,2...1,3, однако все равно криволинейность траектории точки контакта остается.

Получить траекторию точки контакта максимально приближенную к прямой можно, применив специальные равноэластичные подвески (k_э ≈ 1), но они более сложные и дорогие, чем обычные неравноэластичные, поэтому их применение ограничено небольшими опытными участками. Вследствие этого, техническая мысль направлена на то, чтобы при более простой и дешевой конструкции подвески получить траекторию точки контакта близкую к прямолинейной. И такой способ есть. В несколько упрощенном виде он сводится к следующему.

Если расположить контактный провод между точками 1–5 по параболе со стрелой провеса f_к=∆h_сп−∆h₁ (которую мы будем называть оптимальной), то контактный провод будет подниматься токоприемником в пределах этой зоны до такого же уровня, что и в опорных зонах, как это показано на рисунке 91.

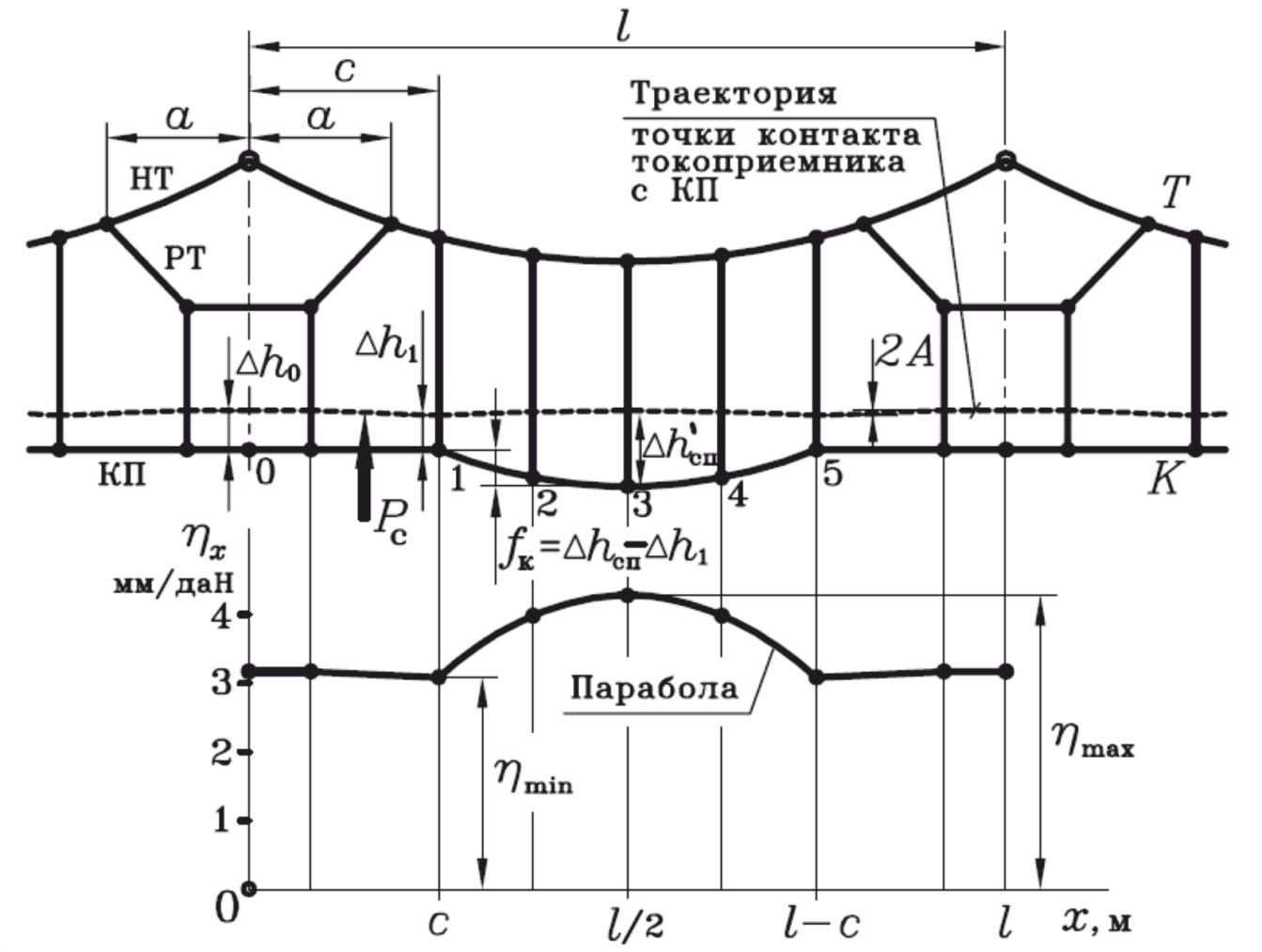
Рисунок 91 – Выравнивание траектории точки контакта токоприемника и контактного провода

В этом случае P_к=P_с+P_дин≈P_с, траектория точки контакта выравнивается и приближается к прямолинейной, т.е. мы получаем то, чего хотели добиться. При расположении контактного провода с определенной стрелой провеса характер изменения эластичности в пролете остается примерно таким же, как и при беспровесном положении.

Этот способ выравнивания траектории точки контакта токоприемника с контактным проводом, при своей кажущейся простоте, имеет следующие основные недостатки:

1. Траектория точки контакта близка к прямолинейной только при расчетных значениях P_к, 2a, c и f_к.

2. Если на одном и том же участке обращаются разные типы ЭПС, на них могут быть применены разные типы токоприемников с разными P_c. Поэтому для одного и того же пролета, для токоприемников типа Л отжатия ∆h₀, ∆h₁ и ∆h_сп, и соответственно f_к будут иметь одни значения, а для токоприемников типа Т – другие. Поэтому при разных ЭПС только для одного типа токоприемников и скорости движения траектория точки контакта будет близка к прямолинейной, а для других типов токоприемников эта траектория будет в разной степени отличаться от прямолинейной. Какую в данной ситуации выбрать оптимальную стрелу провеса f_к? Для более тяжелого случая т.к. P_дин=m_тd2y/dt2.

3. Монтаж и регулировка подвески с заданным провесом контактного провода значительно сложнее, чем при беспровесном положении.

Существует способ, позволяющий снизить трудоемкость, мы уже говорили о нем: монтаж КП в беспровесном положении при повышенном натяжением несущего троса, а затем снижение натяжения НТ до номинального.

Несмотря на эти недостатки, практика эксплуатации подвесок с заданной стрелой провеса контактного провода показала, что в этом случае повышенные трудозатраты на монтаж и регулировку окупаются за счет большего срока службы КП.

Кроме того, есть еще одно важное соображение. При износе контактного провода в процессе эксплуатации его стрела провеса меняется т.к. уменьшается вес КП, уменьшается стрела провеса НТ, а с ним и КП. Если при монтаже нового КП заранее задана положительная стрела провеса, это позволит избежать отрицательных стрел провеса при износе.