Учет изменения зигзагов при перемещении консолей и фиксаторов.

При изменениях температуры изменяются длины проводов, что приводит к перемещению консолей и фиксаторов на опорах (вращению относительно узлов крепления).

При полукомпенсированной подвеске перемещается только дополнительный фиксатор, при компенсированной – консоль вместе с фиксатором. Это проиллюстрированно на рисунке 74.

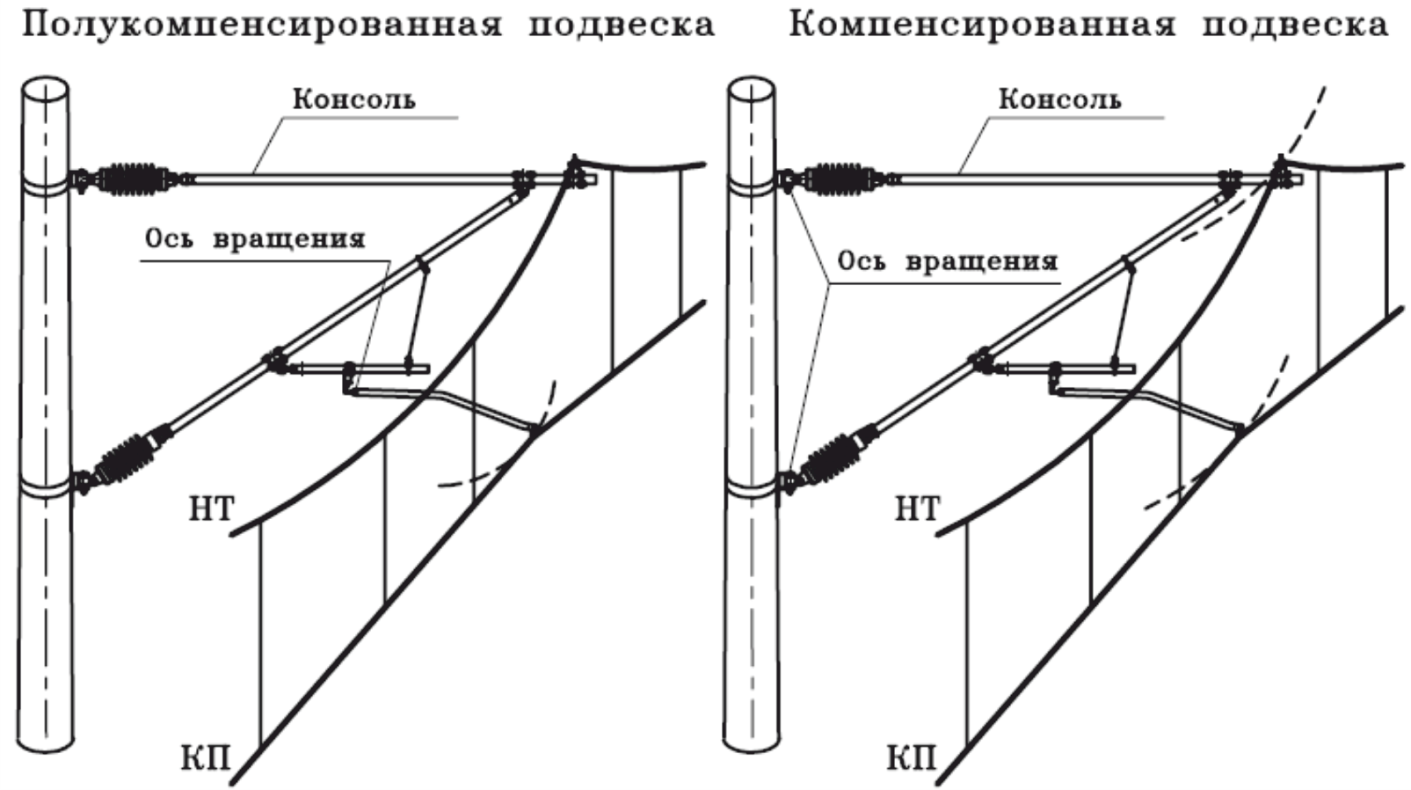
Рисунок 74 – Перемещение консолей и фиксаторов на опорах

При вращении консолей или фиксаторов изменяется зигзаг КП b, как это показано на рисунке 75.

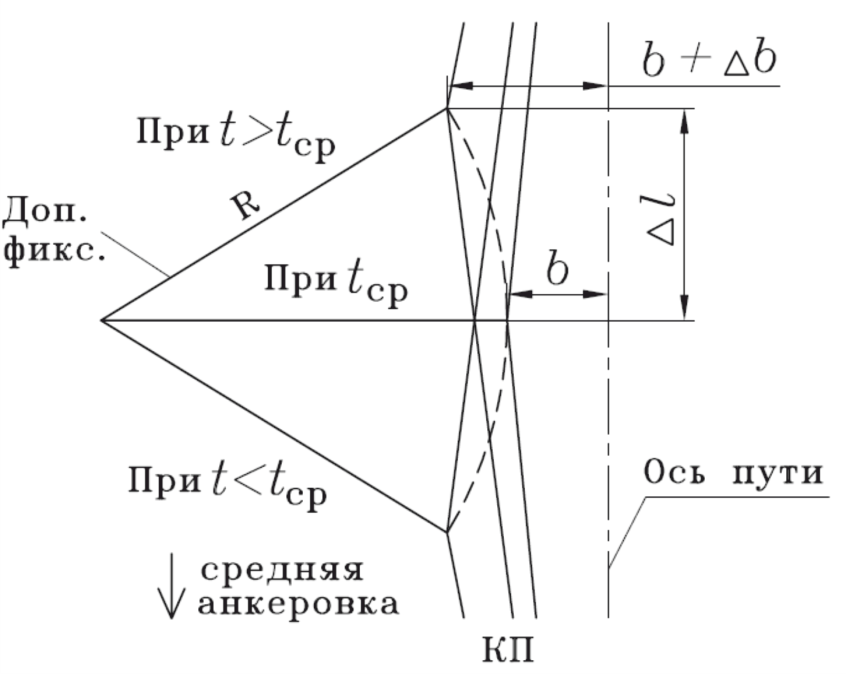
Рисунок 75 – Изменение зигзага КП при вращении консолей и фиксаторов

Изменение зигзага составит

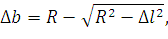
(140)

где R – радиус вращения (для полукомпенсированной подвески – длина дополнительного фиксатора, для типовых фиксаторов R=1,2 м), м;

∆l – перемещение контактного провода при изменении температуры, м.

В соответствии с ПУТЭКС [5], зигзаг рабочего КП b на прямых участках не должен превышать 400 мм, на кривых – 500 мм.

Номинальный зигзаг контактного провода при средней температуре на прямых участках составляет 300 мм.

Длина а.у. и номинальные зигзаги при средней температуре должны выбираться таким образом, чтобы при крайних значениях температур они не превышали максимально допускаемые значения.

С учетом всех ограничений максимальная длина а.у. на прямых составляет около 1500 м (2х750 м) для полукомпенсированных подвесок и около 1600 м (2х800 м) для компенсированных. На кривых допустимая длина уменьшается. Для скоростных подвесок длины а.у. принимаются меньше (например, в КС-200 – 2х700 м).

4.5. Сопряжения анкерных участков

В местах, где токоприемники переходят с КП одного а.у. на КП следующего а.у., монтируют сопряжения анкерных участков. Сопряжения должны обеспечивать плавный переход токоприемников с одного КП на другой при установленной скорости движения поездов, а также работу компенсирующих устройств в анкеровках проводов и допускать взаимное продольное перемещение проводов контактной подвески при изменении температуры.

Сопряжения анкерных участков могут быть неизолирующими (сопряжения без секционирования, которое изображено на рисунке 76) – только с механическим разделением цепных подвесок, и изолирующими (сопряжения с секционированием, изображенное на рисунке 77), в которых, кроме механического, осуществляется и электрическое разделение.

Рисунок 76 – Схема трехпролетного неизолирующего сопряжения а.у. на прямом участке пути

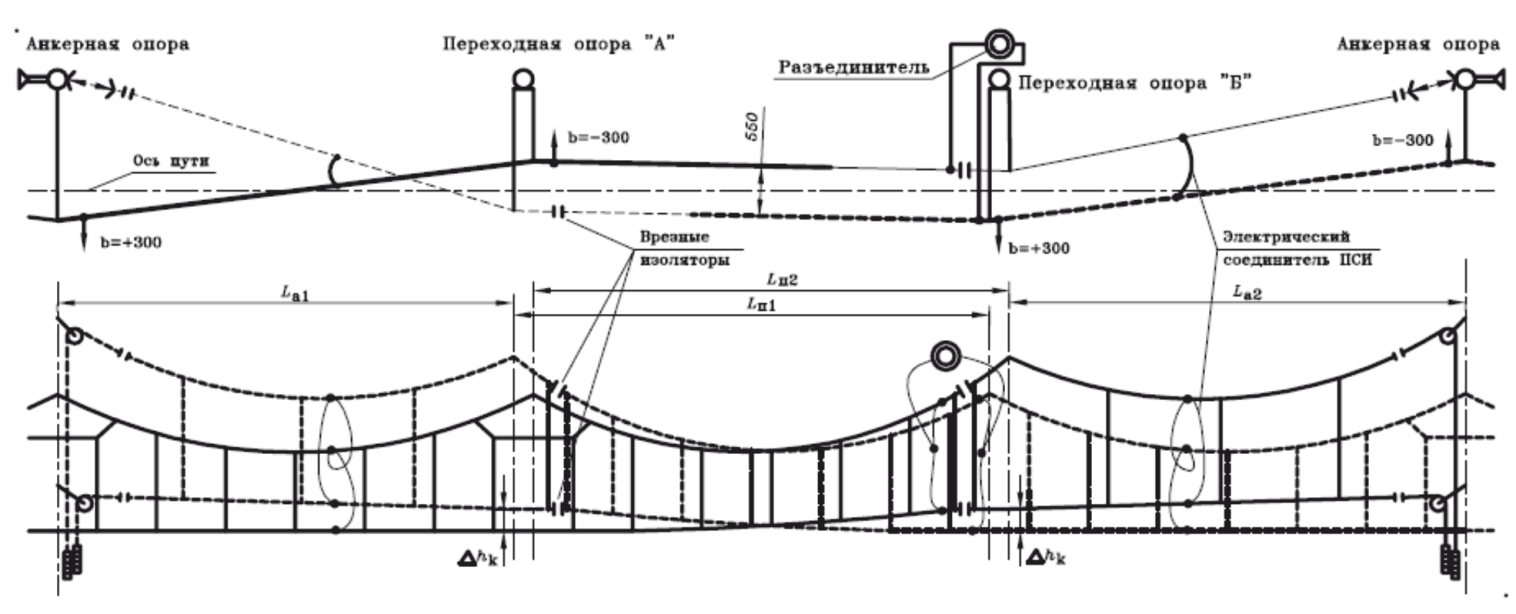
Рисунок 77 – Схема трехпролетного изолирующего сопряжения анкерных участков на прямом участке пути

Неизолирующие сопряжения чаще всего выполняются в трех пролетах. Реже применяются четырехпролетные и пятипролетные сопряжения. На станционных путях, на которых скорость не превышает 50 км/ч, могут применяться также двухпролетные сопряжения (их применение допускается до реконструкции станции).

Рассмотрим расположение КП на трехпролетном сопряжении а.у. без секционирования и с секционированием.

Сопряжение выполнено между двумя анкерными опорами и включает две переходные опоры «А» и «Б». Контактные подвески разных а.у. пересекаются у переходной опоры «А».

На схемах в плане жирными линиями обозначены рабочие участки КП (где токоприемник должен находиться в контакте с КП), тонкими – нерабочие. Переход токоприемника с одного провода на другой происходит в переходном (среднем) пролете. В этом пролете каждый из КП по высоте регулируют так, чтобы у переходной опоры нерабочий контактный провод располагался выше рабочего на величину, которую мы будем обозначать ∆h_k . Величина ∆h_k выбирается больше, чем максимально возможное отжатие токоприемником рабочего КП. На неизолирующих сопряжениях обычно ∆h_k = 300 мм, на изолирующих ∆h_k=350...500 мм в зависимости от конструкции врезных изоляторов (токоприемник не должен задеть изолятор ни при каких условиях).

Расстояние между контактными подвесками в плане на неизолирующих сопряжениях принимается равным 100 мм (между ближайшими контактными проводами разных подвесок). На изолирующих сопряжениях это расстояние увеличивается для предотвращения образования электрической дуги до 400…550 мм (в зависимости от напряжения – 3 или 25 кВ, а также того, нормально замкнут или нормально разомкнут разъединитель).

Для поддержания требуемого натяжения компенсированных проводов контактных подвесок в их анкеровках устраивают компенсаторы температурных перемещений, как правило, грузокомпенсаторы.

На неизолирующем сопряжении надежное электрическое соединение между а.у. осуществляется с помощью продольных электрических соединителей (ПРС), как правило, из провода М-95 или МГ-95.

На рисунке 78 приведен вариант конструктивного исполнения продольного электрического соединителя (ПРС) на неизолирующем сопряжении из провода М-95 «баран»:

Рисунок 78 – Вариант конструктивного исполнения продольного электрического соединителя на неизолирующем сопряжении из провода М-95

На изолирующем сопряжении электрическое соединение двух подвесок (двух секций) осуществляется по необходимости, для чего применяются специальные разъединители с моторным или ручным приводом. В соответствии со схемой питания и секционирования участка разъединитель может быть нормально разомкнут или нормально замкнут. На рисунке 79 приведено возможное расположение этого разъединителя.

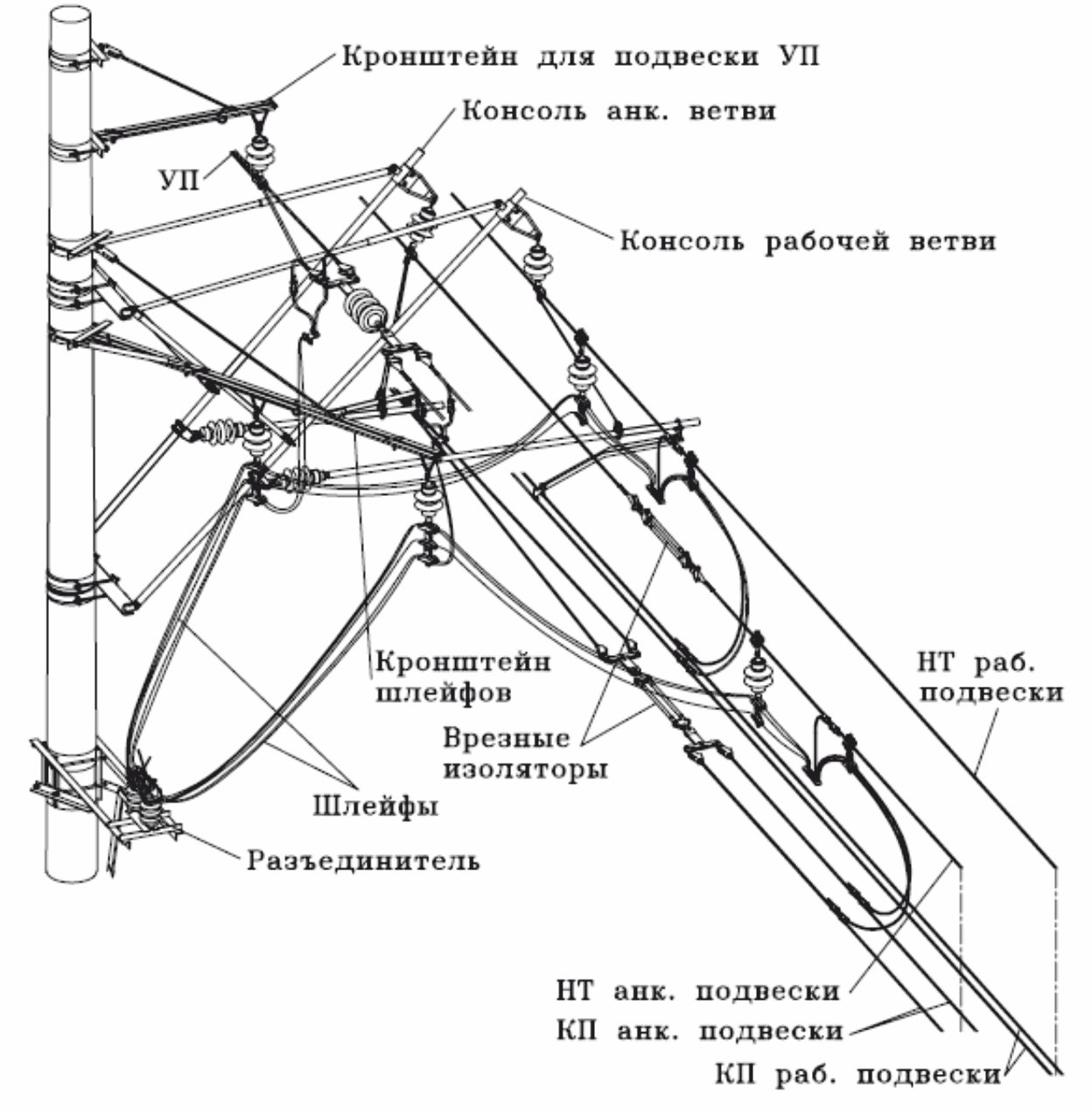
Рисунок 79 – Расположение разъединителя на переходной опоре

Рассмотрим схемы подъема КП на неизолирующем и изолирующем сопряжении, приведенные на рисунках 80 и 81.

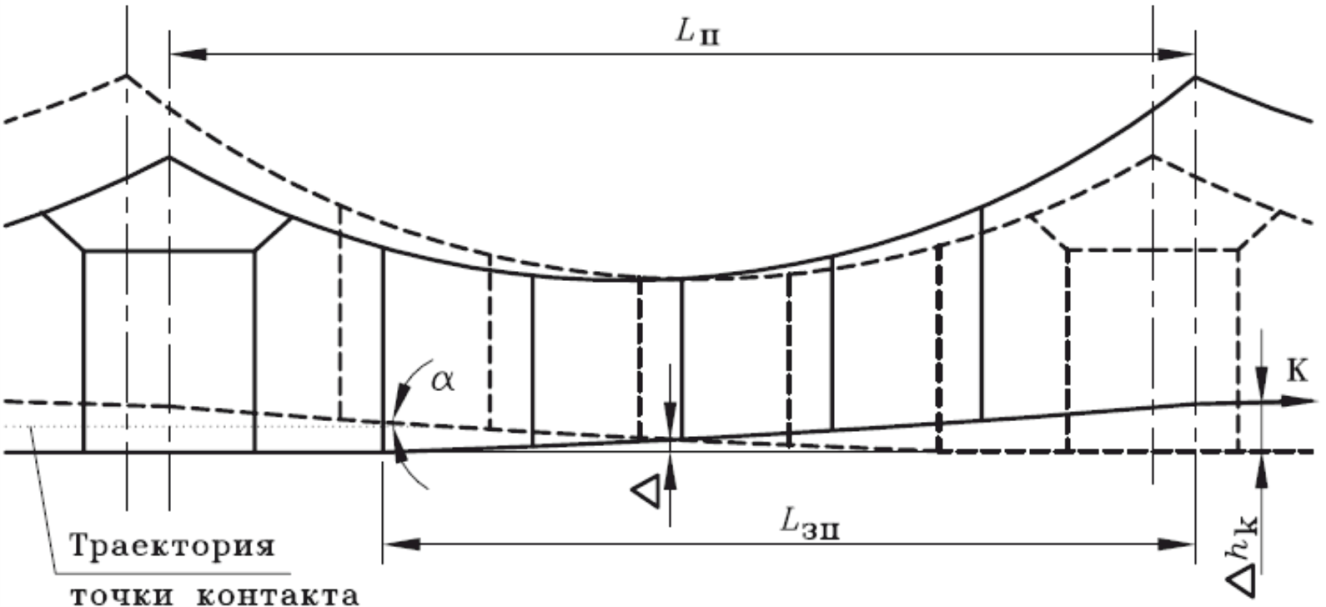
Рисунок 80 – Схема подъема КП на неизолирующем сопряжении а.у.

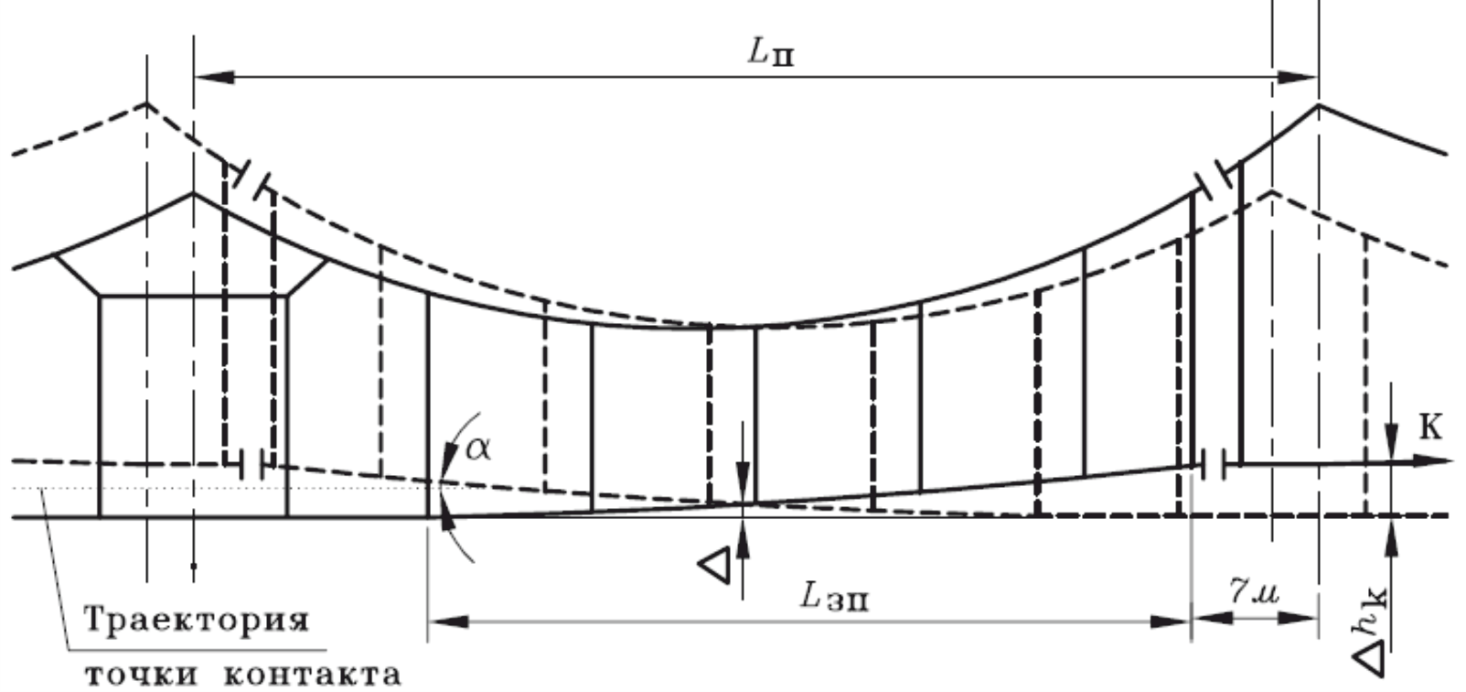
Рисунок 81 – Схема подъема КП на изолирующем сопряжении а.у.

Подъем КП в переходных пролетах сопряжений рекомендуется осуществлять по параболе, т.к. это позволяет обеспечить минимальный угол α, под которым токоприемник встречается с ниспадающей ветвью контактного провода следующей по ходу движения подвески.

Подъем контактного провода начинают от одной из струн в пролете (для удобства монтажа). Расчетную величину ∆h_k на неизолирующем сопряжении необходимо обеспечить у опоры (под фиксатором анкеруемой ветви), а на изолирующем – уже в месте врезки изолятора в КП в переходном пролете.

Минимальная длина зоны подъема КП:

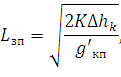
(141)

где 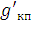= (0,7...0,8)g_кп с учетом натяжения струн, Н/м.

Длину переходного пролета неизолирующих сопряжений стараются делать равной максимально допускаемой длине промежуточного пролета в данном месте.

Длину переходного пролета изолирующих сопряжений сокращают на 25% от максимально допускаемой длины промежуточного пролета в данном месте по ветроустойчивости. (25% – норматив для прямых и кривых радиусом более 1500 м. На кривых меньшего радиуса допускаются меньшее сокращение).

Вообще, чем больше длина переходного пролета – тем лучше. Если по условиям ветроустойчивости или допустимых габаритов нельзя выполнить достаточно большую длину пролета, чтобы обеспечить необходимую плавность перехода токоприемника с КП одной подвески на КП другой подвески в одном переходном пролете, то приходится делать большее число переходных пролетов (четырех- и пятипролетные сопряжения). Основными критериями плавности пере- хода токоприемника являются:

1. Угол α, под которым токоприемник встречается с ниспадающей ветвью КП следующей по ходу движения подвески. Угол α должен быть как можно меньше (обычно, не более 0,70);

2. Величина ∆ («птица») – возвышение точки пересечения осей КП сопрягающихся подвесок относительно прямой, соединяющей между собой оси рабочих КП на обеих переходных опорах.

∆ должна быть не более 40 мм. Самый лучший вариант – если ∆=0. Для этого подъем КП должен начинаться в середине переходного пролета, что не всегда можно сделать.

Для типовых контактных подвесок при скоростях движения до 120 км/ч по условию плавности перехода токоприемника с КП одной подвески на КП другой подвески, рекомендуются следующее число переходных пролетов в зависимости от их длины, чтобы обеспечить указанные параметры α и ∆.

Неизолирующие сопряжения:

40 ≤ Lп ≤ 70 – 1 (трехпролетное сопряжение);

35 ≤ Lп < 40 – 2 (четырехпролетное сопряжение);

20 ≤ Lп < 35 – 3 (пятипролетное сопряжение).

Изолирующие сопряжения:

55 ≤ Lп ≤ 70 – 1 (трехпролетное сопряжение);

45 ≤ Lп < 55 – 2 (четырехпролетное сопряжение);

28 ≤ Lп < 45 – 3 (пятипролетное сопряжение).

При больших скоростях движения эти границы ужесточаются, т.е. четырех- и пятипролетные сопряжения применяются при больших длинах переходных пролетов.

Сопряжения компенсированной и полукомпенсированной подвесок не допускаются. Стыковка должна осуществляется у средней анкеровки компенсированной контактной подвески так, чтобы одна половина анкерного участка работала как компенсированная, вторая – как полукомпенсированная.

5. Взаимодействие токоприемника и контактной подвески

5.1. Эластичность контактной подвески

Контактные подвески являются эластичными конструкциями.

Эластичность – это свойство контактных подвесок упруго реагировать (сопротивляться) на воздействие внешних сил, изменяя при этом свою геометрию и положение в пространстве, и возвращаться в исходное положение, которое они занимали до воздействия внешних сил, после прекращения воздействия. Возвращение подвески в исходное положение представляет собой колебательный процесс, скорость затухания которого зависит от конструктивных особенностей.

Эластичность контактной подвески в рассматриваемой точке характеризуется отжатием контактного провода под действием приложенной к нему снизу вверх вертикальной силы. Эластичность оценивается числом η, измеряемым, как правило, в мм/Н, показывающем, на сколько мм поднимется контактный провод при воздействии на него силы в 1 Н:

(142)

где h_x – отжатие контактного провода в точке приложения силы, мм;

P – сила нажатия, Н.

Иногда применяют обратную величину, называемую жесткостью контактной подвески:

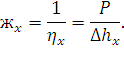
(143)

По характеру изменения эластичности в пролете контактные подвески могут быть равно- и неравноэластичными. Контактные подвески, у которых эластичность во всех точках пролета имеет одно и то же значение называют равноэластичными. Подвески, у которых значение эластичности изменяется в пределах пролета, называют неравноэластичными. Подавляющее большинство подвесок, применяемых в России и в мире (в том числе и подвески для высоких скоростей движения), являются неравноэластичными.

Для достижения примерно одинаковой эластичности во всех точках пролета приходится существенно усложнять конструкцию подвески. С известной долей приближения равноэластичными могут быть выполнены двойные контактные подвески (лучше всего – вантовая), рычажная и некоторые другие «экзотические» конструкции подвесок.

Изменение эластичности в пролете определяется, в основном, изменением упругого влияния НТ на подъем КП в пределах пролета.

Изменение упругого влияния НТ в пределах пролета является следствием жесткого подвешивания НТ в опорных узлах. Наибольшее влияние на подъем КП оказывает НТ в средней части пролета, по мере приближения к опорам это влияние уменьшается. Для подвески с простой опорной струной под опорами это влияние становится равным нулю.

Изменение эластичности в пролете характеризуется коэффициентом неравномерности эластичности k_э:

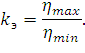
(144)

В международной практике чаще используют относительную неравномерность эластичности в пролете, выраженную в процентах:

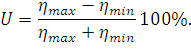
(145)

В идеальном случае k_э=1 или U=0 (равноэластичные подвески).

Для неравноэластичных подвесок коэффициент неравномерности эластичности (или относительная неравномерность) является одним из косвенных показателей, по которым можно судить о допускаемой скорости движения по подвеске.

Например, по мнению некоторых отечественных специалистов, для скоростей до 200 км/ч коэффициент неравномерности эластичности должен быть не более 1,33.

Международными нормативными документами определены требования к относительной неравномерности эластичности в зависимости от максимальной скорости движения. Например, в соответствии с нормативным документом UIC-799 Международного союза железных дорог, для контактных рессорных подвесок переменного тока при скоростях движения 200-230 км/ч относительная неравно- мерность должна быть менее 20%, при скоростях 230-300 км/ч – менее 10%.

5.1.1. Характер изменения эластичности в пролете и его влияние на траекторию точки контакта токоприемника с контактным проводом

Каков же характер изменения эластичности в пролете

и как влияет изменение эластичности подвески в пролете на траекторию точки контакта токоприемника с КП?

Рассмотрим эти вопросы применительно к небольшим скоростям движения (рассуждения будут допустимы при скоростях не более 120 км/ч). При больших скоростях характер траектории точки контакта в значительной степени определяется сложными динамическими процессами, а не только распределением эластичности, которое мы определяем в статике.

Рассмотрим контактную подвеску с простыми опорными струнами, приведенную на рисунке 82.

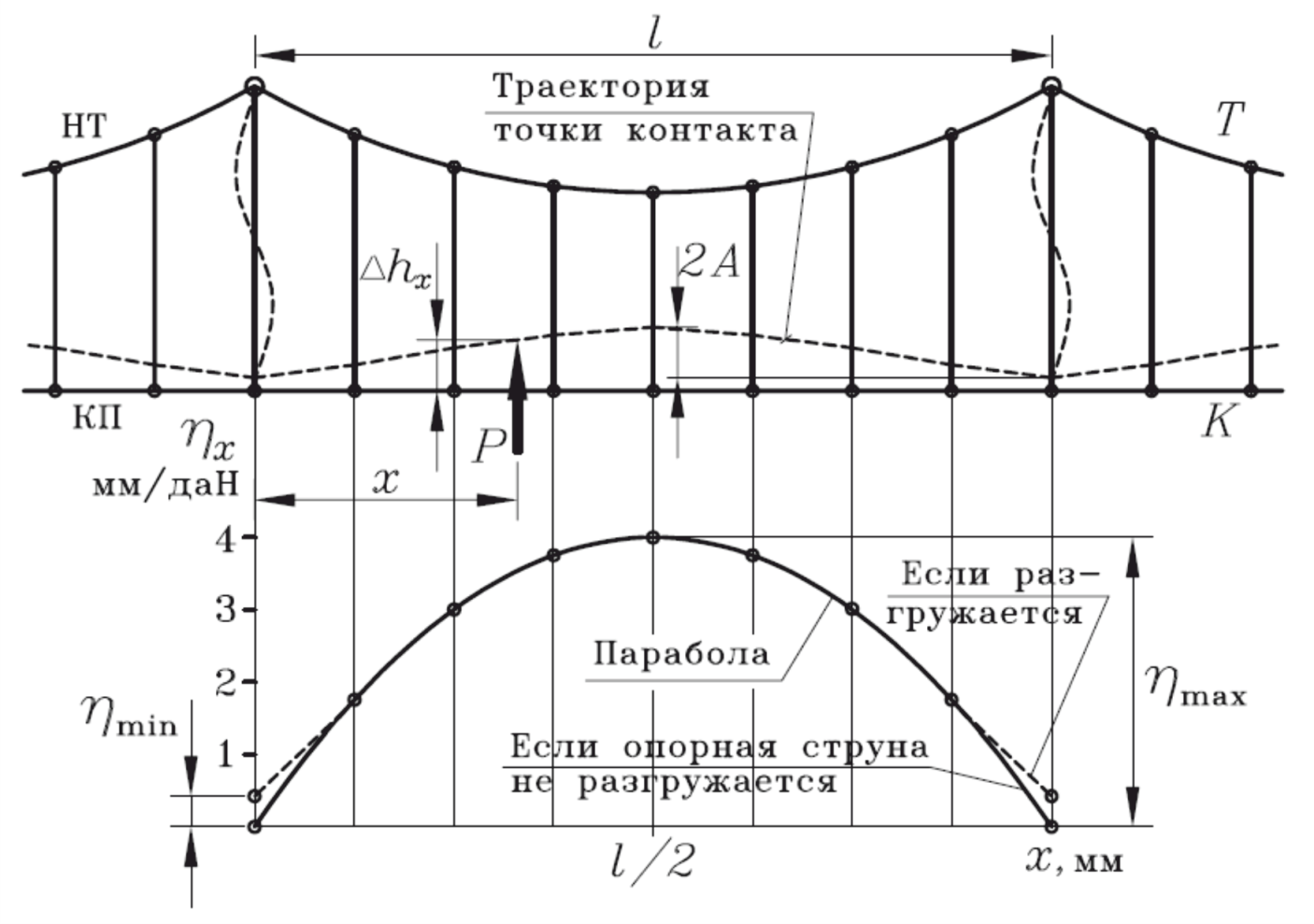
Рисунок 82 – Траектория движения точки контакта токоприемника и контактного провода контактной подвески с простыми опорными струнами

Если опорные струны не разгружаются распределение эластичности в пролете приближенно описывается следующим выражением:

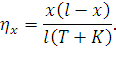
(146)

Если опорные струны разгружаются – вблизи опор это выражение будет несправедливо.

Эластичность в середине пролета равна:

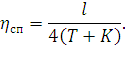
(147)

Пока приводим эти формулы без вывода.

В большей части пролета траектория точки контакта токоприемника с КП в определенном масштабе повторяет кривую изменения эластичности подвески в пролете, т.е. характер изменения эластичности подвески определяет характер траектории точки контакта токоприемника с КП.

Качество взаимодействия токоприемника с контактной подвеской (качество токосъема и интенсивность износа КП и токосъемных пластин токоприемника) косвенно оценивается по следующим критериям:

а) характеру траектории точки контакта токоприемника с КП (чем она ближе к прямой, тем лучше качество токосъема);

б) изменению контактного нажатия P_к (усилия в контакте токоприемника с контактным проводом) относительно оптимального его значения (чем в меньших пределах меняется P_к, тем лучше качество токосъема).

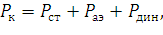
(148)

где P_ст – статическая составляющая контактного нажатия, Н;

P_аэ – аэродинамичаская составляющая контактного нажатия, P_аэ=kV 2, Н;

P_дин – динамическая составляющая контактного нажатия, Н.

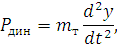
(149)

где m_т – приведенная масса токоприемника, кг,

d²y/dt² – ускорение приведенной массы при движении в вертикальном направлении, м/с².

При определенной и постоянной скорости движения и высоте КП изменение P_к происходит за счет P_дин. Значение и знак P_дин зависит от приведенной массы токоприемника и значения и знака ускорения этой приведенной массы.

Значение ускорения зависит от размаха колебаний точки контакта токоприемника с КП в пролете 2А. Чем меньше размах колебаний 2А, тем меньше P_дин и тем меньше пределы изменения P_к.

Размах колебаний зависит от изменения эластичности – чем в меньших пределах меняется эластичность, тем меньше размах колебаний. Вот почему стремятся выравнивать эластичность обычных подвесок в пролете настолько, насколько это возможно и целесообразно с технической и экономической точек зрения, используя разные способы выравнивания. Это выравнивание осуществляют за счет:

1. увеличения эластичности опорного узла (применения смещенных околоопорных струн вместо простых опорных, применение рессорного троса, увеличение его длины и натяжения);

2. уменьшения эластичности в середине пролета (увеличения натяжений НТ и КП, уменьшения длины пролета).

Применяют эти способы одновременно или по отдельности.

Сравним характер изменения эластичности и траектории точки контакта для контактной подвески с простыми опорными струнами, приведенной на рисунке 82, со смещенными струнами (рисунок 83) и с рессорным тросом (рисунок 84).

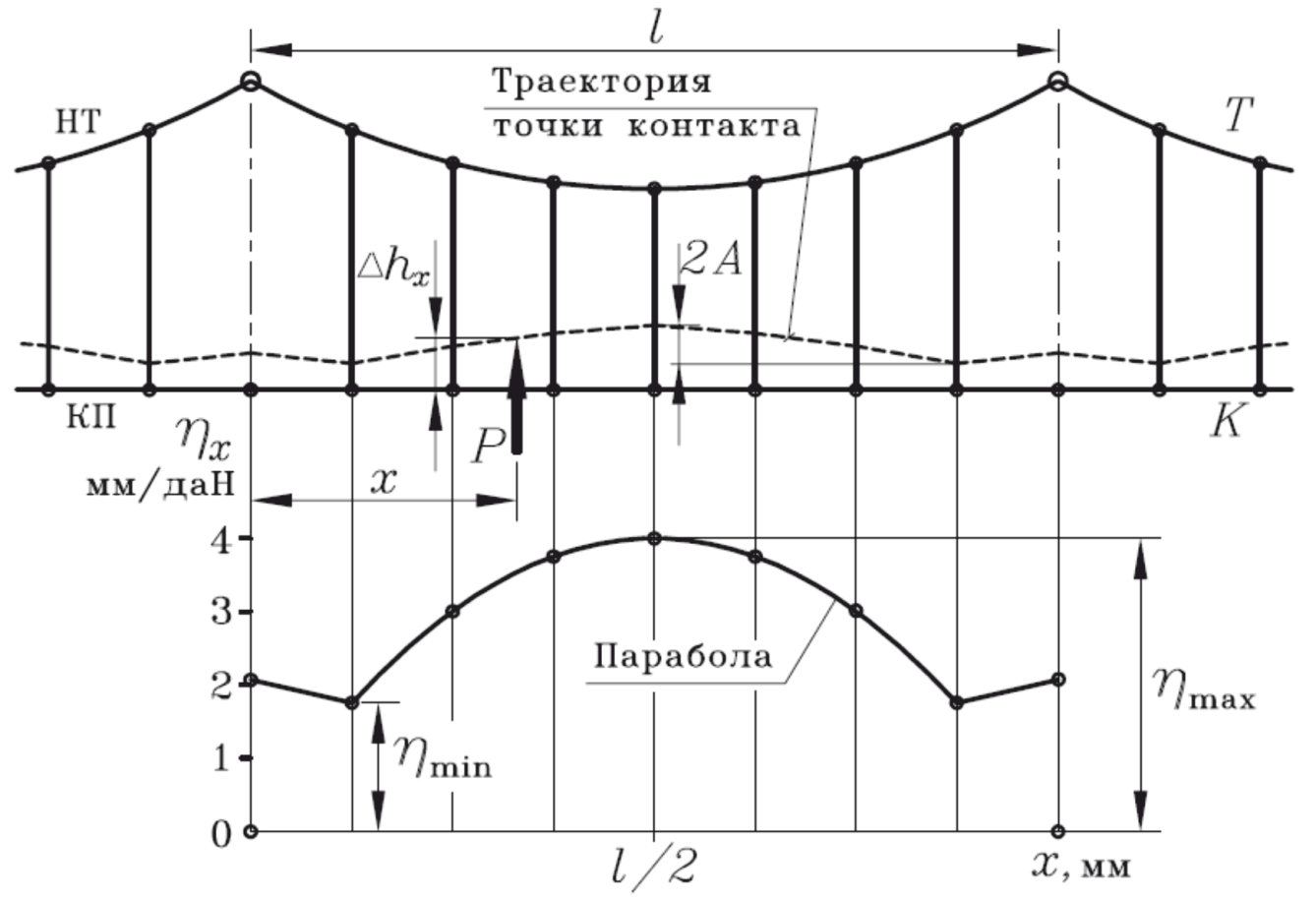
Рисунок 83 – Траектория движения точки контакта токоприемника и контактного провода контактной подвески с разнесенными опорными струнами

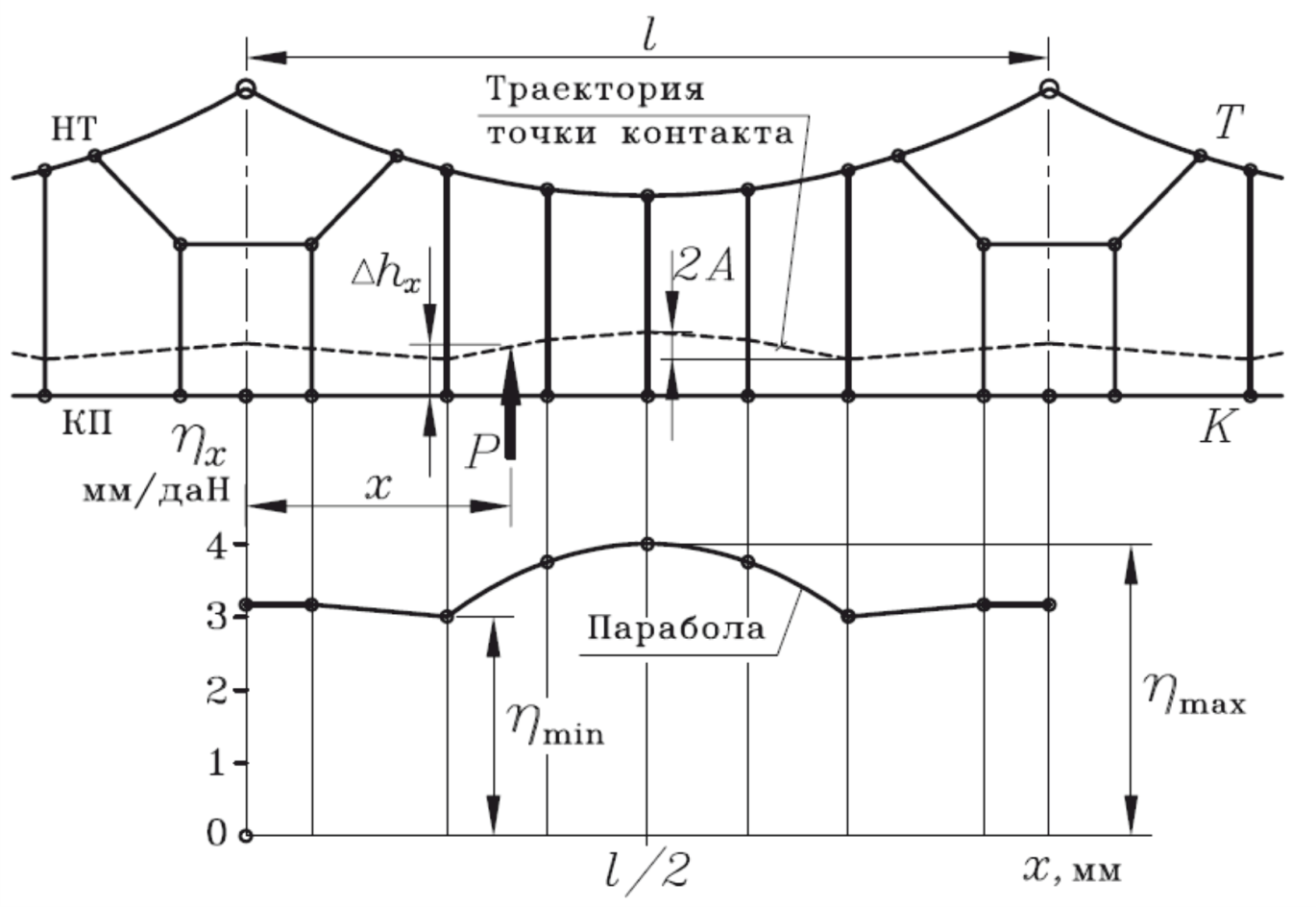
Рисунок 84 – Траектория движения точки контакта токоприемника и контактного провода контактной подвески с рессорным тросом

5.1.2. Определение эластичности контактной подвески

Определение эластичности простой контактной подвески (свободно подвешенного провода)

Рассмотрим пролет простой контактной подвески (свободно подвешенного провода) с жесткими опорными точками, приведенный на рисунке 85.

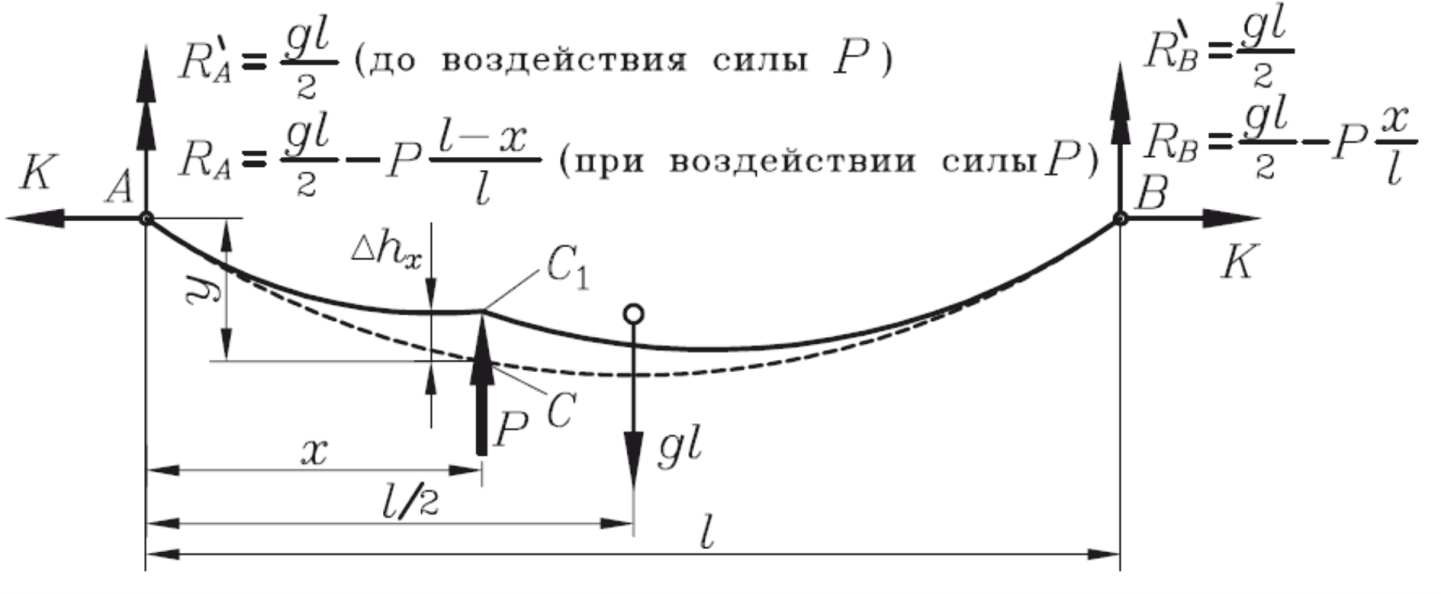
Рисунок 85 – Расчетная схема для определения эластичности свободно подвешенного провода

Вертикальная сила P , приложенная на расстоянии x от опоры, вызывает подъем (отжатие) провода на высоту ∆h_x и разгрузку опор.

Рассмотрим часть пролета от точки A до точки приложения силы (рисунок 86).

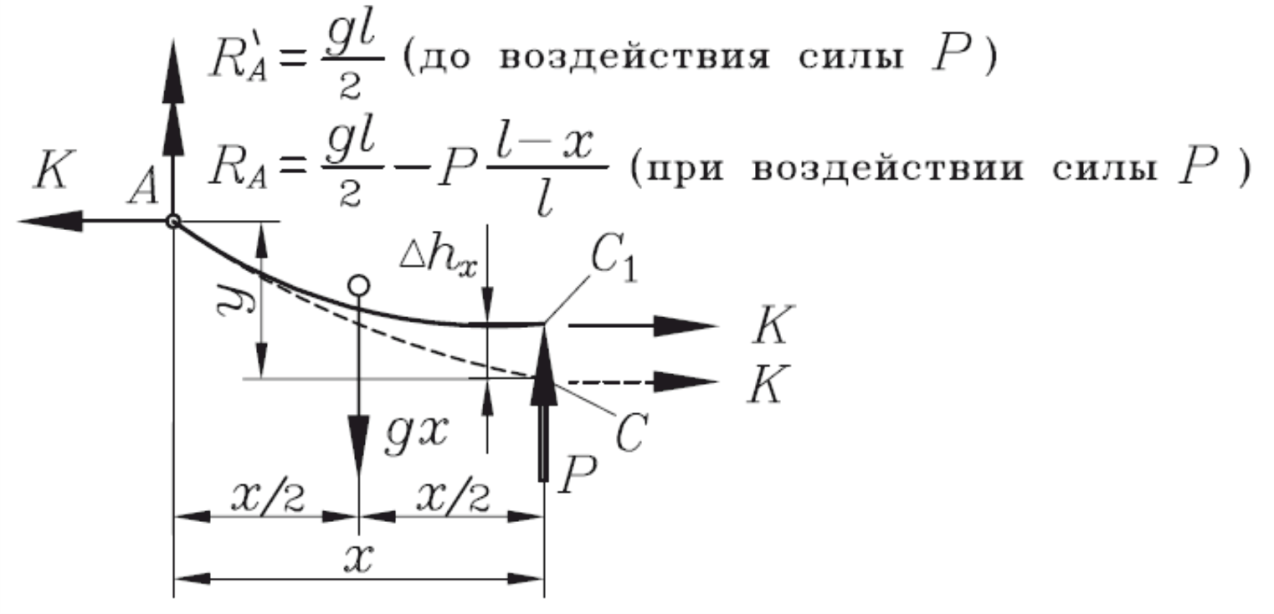
Рисунок 86 – Расчетная схема для определения эластичности свободно подвешенного провода с заменой правой части пролета реакциями

Запишем уравнения равновесия для этой части пролета, приравнивая сумму моментов относительно точки C нулю, до и после приложения силы.

До воздействия силы P:

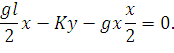
(150)

При воздействия силы P:

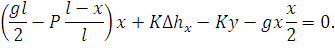
(151)

Из (151) вычтем(150), получим:

(152)

Уравнение (152) означает, что сумма изменений моментов действующих сил относительно точки C также равна нулю (т.к. до и после приложения силы P провод в рассматриваемой части пролета находится в равновесии).

Из (152) получаем

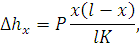
(153)

откуда можем записать выражение для эластичности:

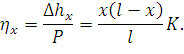
(154)

Таким образом, эластичность в пролете простой подвески изменяется по параболе от 0 (у жестких точек закрепления) до максимального значения в середине пролета, которое легко найти, подставив в (154) x = l/2:

(155)