Задача Левича.
Рассмотрим набегание потока жидкости на пластину из труднорастворимой соли, которая растворяется с течением времени.
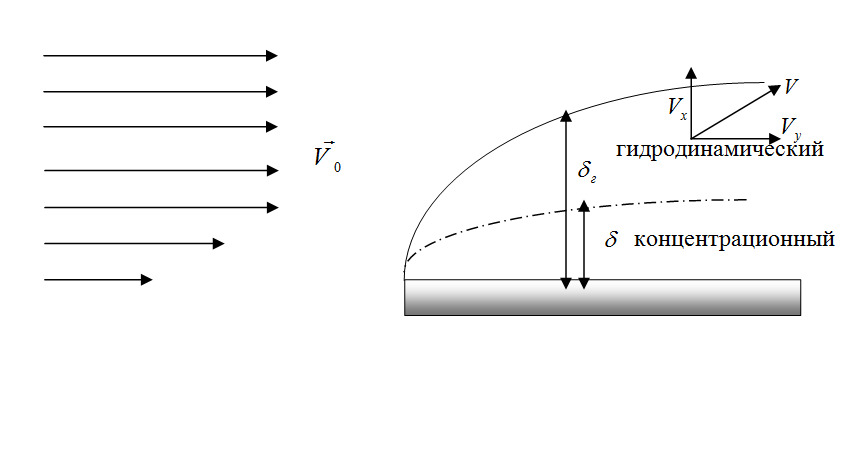
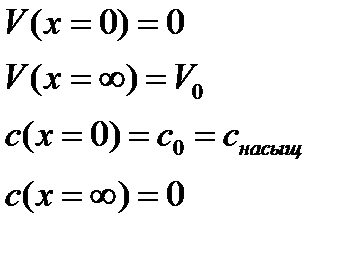
 толщина слоя.
толщина слоя.
Для того чтобы описать поведение такой системы, необходимо решить совместно уравнение Навье-Стокса и уравнение конвективной диффузии. В данном случае, эти 2 системы уравнений не будут сцеплены между собой, так как имеется только вынужденная конвекция.
Если в системе можно пренебречь объемной силой F, тогда связь между уравнениями Навье-Стокса и конвективной диффузии теряется.
Для нахождения поля скоростей и поля концентрации сначала нужно решить систему уравнений Навье-Стокса и найти распределение скорости, а затем подставить найденное распределение скорости в уравнение конвективной диффузии и найти распределение поля концентрации. Эту задачу для данного случая решил Левич в 1950 году.
Уравнения, описывающие процесс изменения концентрации:
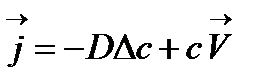 – уравнение конвективной диффузии, – уравнение конвективной диффузии,
| (3.1) |
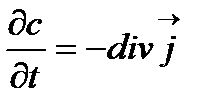 , – закон сохранения , – закон сохранения
| (3.2) |
Граничные условия скорости:
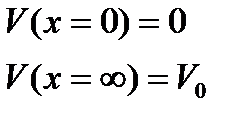
| (3.3) |
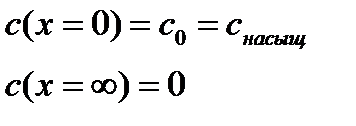
| (3.4) |
Уравнения (3.1), (3.2) можно объединить, подставив уравнение (3.1) в уравнение (3.2). Получим:
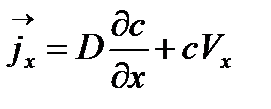
| (3.5) |
(Если скорость жидкости ламинарная, то нормальная составляющая скорости равна нулю, т е 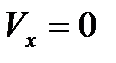 )
)
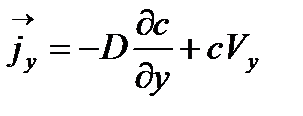
| (3.6) |
Режим стационарный, т е:
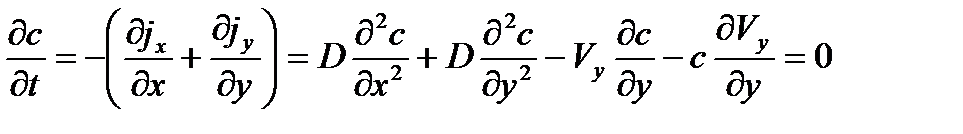
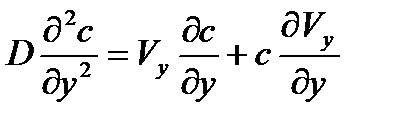
Учитывая, что некоторые слагаемые обращаются в ноль, получим:
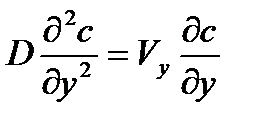
| (3.7) |
Распределение скоростей находятся из уравнений Навье-Стокса
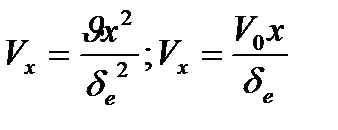
| (3.8) |
Для того, чтоб решить уравнение (3.7), необходимо уравнение (3.8) подставить в (3.7) .(Таким образом, меняющаяся концентрация не влияет на скорость, т е уравнения решаются отдельно.) Решая уравнение Навье-Стокса, получим:
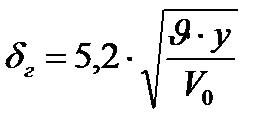 - гидродинамический погранслой (слой, где чувствуется «прилипание») - гидродинамический погранслой (слой, где чувствуется «прилипание»)
| (3.9) |
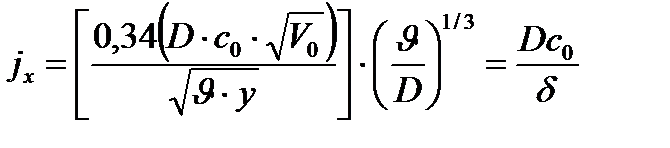 , ,
| (3.10) |
Тогда 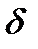 можно выразить через (3.10):
можно выразить через (3.10):
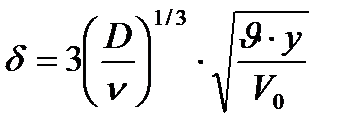 - толщина диффузионного погранслоя - толщина диффузионного погранслоя
| (3.11) |
Сравним (3.9) и (3.11), получим
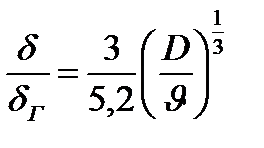
Отсюда, приведя к одной размерности, получим:
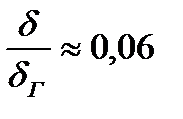
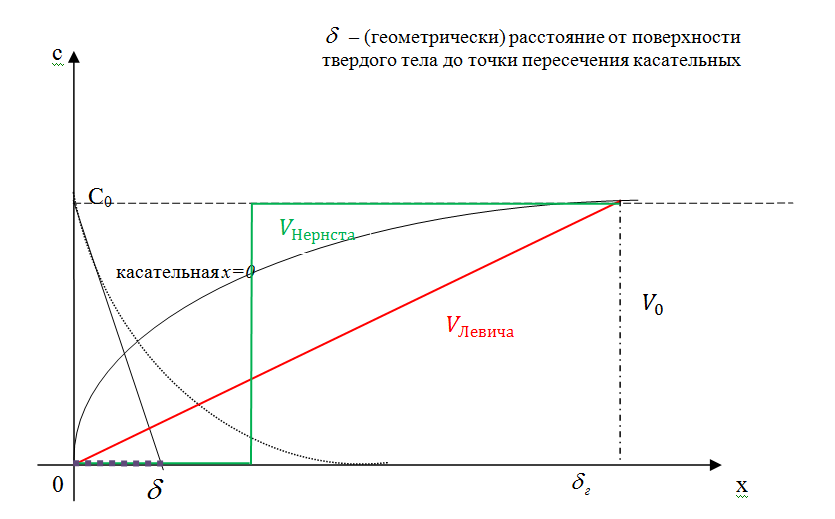
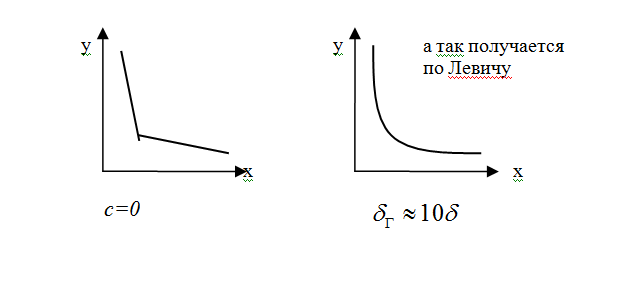
Таким образом, толщина диффузионного концентрационного погранслоя ≈ в 10 раз меньше, чем толщина гидродинамического погранслоя.
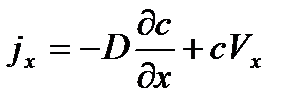
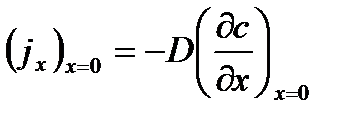 , при x=0, , при x=0,  =0 =0
| (3.12) |
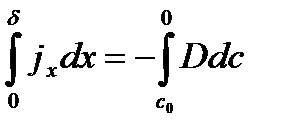
Полагаем, что все изменение концентрации происходит внутри пограничного слоя.
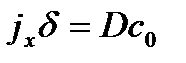
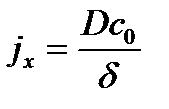 , ,
| (3.13) |
(3.13) было получено путем интегрирования уравнения конвективной диффузии при достаточно грубых упрощениях, а именно, мы предположили, что вблизи поверхности твердого тела имеется тонкий слой, внутри которого 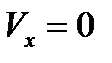 ,а
,а 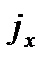 и
и 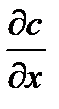 - константы. Такое предположение было сделано Нернстом в 1895 году.
- константы. Такое предположение было сделано Нернстом в 1895 году.
Если сравнить (3.12) и (3.13), то получим: 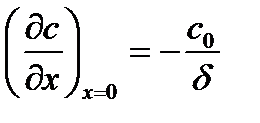
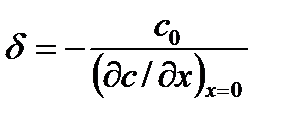
От (3.12) можно перейти к закону Фика: 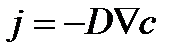
В уравнении Нернста 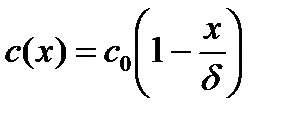 , тогда в (3.13)
, тогда в (3.13)  , получаем линейное уравнение и тогда
, получаем линейное уравнение и тогда
Дата добавления: 2015-10-21; просмотров: 1109;
