Теплопроводность. Закон Фурье.

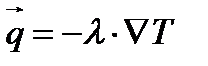– закон Фурье.

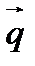- плотность потока тепла

В общем случае:

аналогично предыдущим формулам ,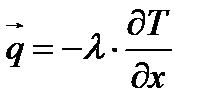

(2.8)

Перенос тепла осуществляется за счет соударения молекул друг с другом, при этом более “горячие” молекулы передают часть своей энергии более “холодным”.

Электродиффузия

Уравнение Нернста-Планка

Если в системе одновременно протекают диффузия и электроперенос, то нужно уравнение, обобщающее законы Фика и Ома.

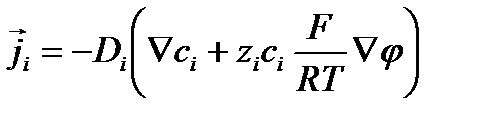- уравнение Нернста-Планка

(2.9)

Это уравнение – суперпозиция двух уравнений: Фика и Ома, выраженных в единой системе единиц.

;

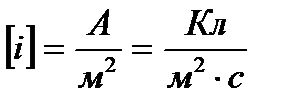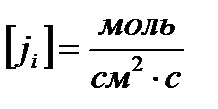
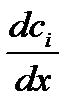и 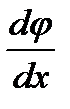- движущие силы.

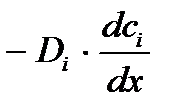- диффузионная составляющая переноса.

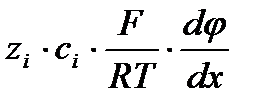- миграционная составляющая переноса.

Пр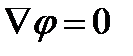и или 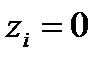уравнение (2.9) сводится к закону Фика.

Упражнение. Показать, что в случае, когда 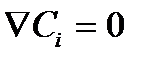, уравнение Нернста-Планка сводится к уравнению Ома.

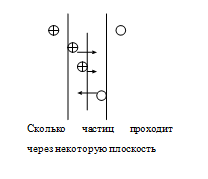
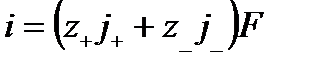- уравнение переноса заряда,

(2.10)

где:

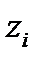- зарядовое число иона

F – число Фарадея,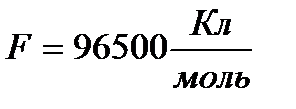

R - газовая постоянная,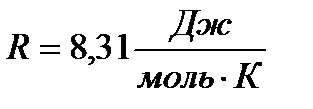

Т - абсолютная температура [T] = K

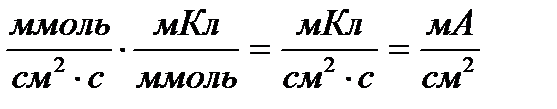
Уравнение (2.10) показывает, что электрический ток в системе складывается из зарядов, перенесенных катионами и анионами (то есть всеми ионами, имеющимися в системе).

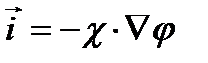- закон Ома

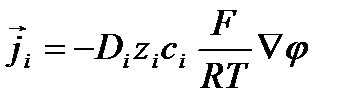- уравнение Нернста-Планка

,

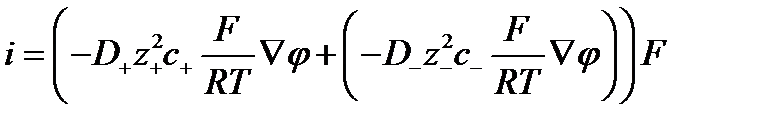
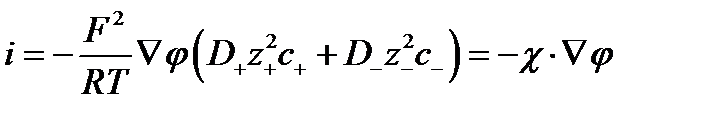(2.11)

Это уравнение имеет тот же вид, что и уравнение Ома в дифференциальной форме.

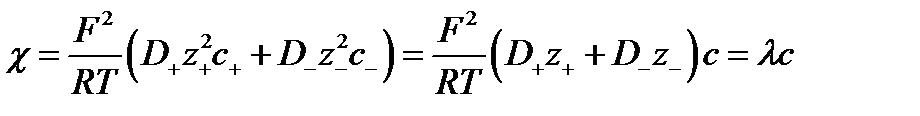– удельная электропроводность раствора

(2.12)

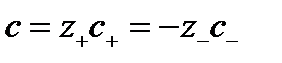- эквивалентная концентрация электролита

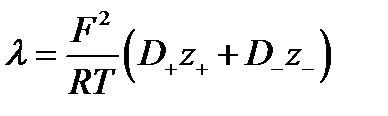- эквивалентная электропроводность раствора

В общем случае многокомпонентного раствора:

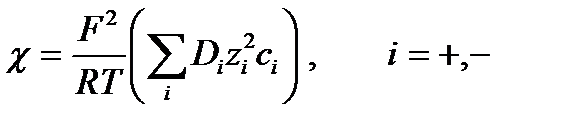
Частный случай – раствор электролита.

Здесь выполняется условие нейтральности:

,

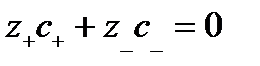(2.13)

Например: :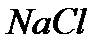

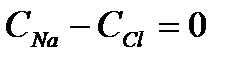
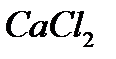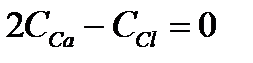: , т.е.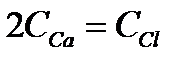

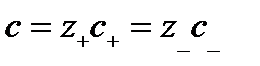- эквивалентная концентрация электролита.

число молей определяется числом частиц.

Тогда уравнение (2.12) можно упростить: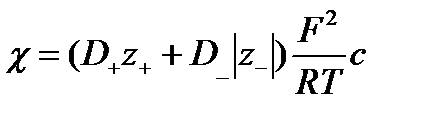

Или 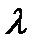- эквивалентная удельная электропроводность,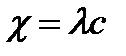

Можно считать, что 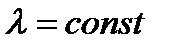и тогда удельная электропроводность раствора прямо пропорциональна его концентрации.